Sorting Algorithms (Edexcel A Level Further Maths): Revision Note
Exam code: 9FM0
Introduction to sorting algorithms
Sorting algorithms arrange items (usually values, letters or words) into ascending or descending order
whilst arranging a (small) list of items is easy for a human being, machines, robots and computers, etc would need programming to do so
as a list of items becomes larger, it becomes increasingly difficult for a human to sort
programming a computer to use a sorting algorithm makes the process both accurate and efficient (first time!)
With sorting algorithms in particular, it is important to stay in 'robot mode'
do not be tempted to take shortcuts or miss parts of the algorithm out because the answer can be 'seen'
follow each step of the algorithm precisely, in order, exactly as a robot would
Bubble sort
What is the bubble sort algorithm?
The bubble sort algorithm arranges items into either ascending or descending order
Items are usually values
but could be letters or words and similar
for questions given in context values will be measures such as weights, lengths, scores or times
How does the bubble sort algorithm work?
Bubble sort works by comparing pairs of items on the working list
the first item is compared to the second, the second to the third, and so on
a swap occurs if a pair of items are not in order
a pair of equal items would not count as a swap
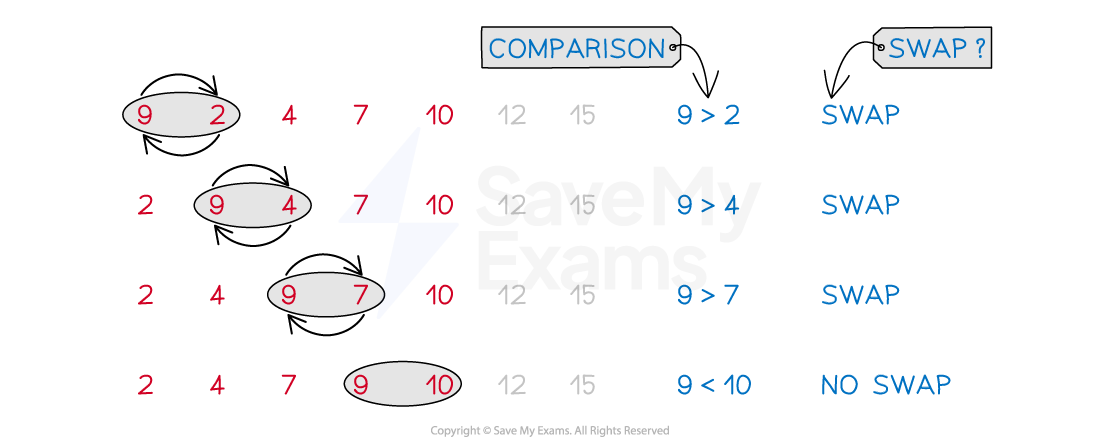
This comparison of pairs and possible swaps continues until the end of the working list is reached
this is called a pass
several passes are usually required to order a list of items
At the end of each pass, the item at the end of the working list is in the correct place
for ascending order, the highest value 'bubbles' to the top
Bubble sort, for
items, is complete when either
a pass involves with no swaps, or,
after the
pass
i.e. when only one item would remain on the working list
so comparisons are neither possible nor necessary
What is the working list?
The working list is the list of items that a pass of the bubble sort algorithm will apply to
For the first pass every item on the list is in the working list
After the first pass, the final item is in the correct place
other items may be too but the algorithm ensures the highest (for an ascending list) or smallest (for descending) item is at the end of the list
this item need not be involved in further comparisons and so it is removed from the working list
After the second pass, the last two items will be in the correct place
After the third pass, the last three items will be correctly sorted, and so on
Reducing the working list by one after each pass helps keep the bubble sort efficient as possible by not requiring unnecessary comparisons
For a list of
items
the first pass will have
items on the working list
the second pass will have
items on the working list
the third pass will have
items on the working list
(if required) the
pass will have 2 items on the working list
Alongside the working list for unordered items, the ordered items may be referred to as the sorted list
The image below shows a list at the end of the second pass of an ascending bubble sort
two items are on the sorted list (12 and 15)
the 10 being in the correct position is irrelevant at this stage ('robot mode'!)
the third pass will confirm its position and that's when it will become part of the sorted list

How do I work out the (maximum) number of passes in the bubble sort algorithm?
For a list of
items
the maximum number of passes will be
this is because after the
pass,
items will be in order, so the last remaining item must be in order too
without actually carrying out a few passes it is hard to predict or work out how many passes bubble sort will need
but it may be possible to tell how many more passes are required when only a few items are out of order
If the item at the end of the list should be at the start then will take
passes
This is because this item will only move one space closer to the start after each pass
How do I work out the (maximum) number of comparisons in the bubble sort algorithm?
For a list of
items
the number of comparisons at each pass will always be one less than the number of items on the working list
the first pass will have
items are on the working list so there will be
comparisons
the second pass will have
comparisons
the
pass will have
comparisons
(if required) the
pass will have 1 comparison
the maximum number of comparisons for the entire bubble sort algorithm would be
or
understanding the logic for the number of comparisons is easier than trying to remember a formula
the final formula,
is quadratic and so bubble sort is of quadratic order
How do I work out the (maximum) number of swaps in the bubble sort algorithm?
For a list of
items
the maximum number of swaps in a pass would be the same as the number of comparisons for that pass
i.e. every comparison results in a swap being made
this would occur if the first item on the working list is the largest (or smallest for descending)
so the maximum number of swaps for the entire algorithm would be needed to if a list started in reverse order
with a small working list it is possible to 'see' or count the number of swaps required for a pass
it can be awkward keeping track in longer lists so be wary of relying on this sort of inspection technique
keeping a tally of swaps as you perform a pass would be more reliable
Examiner Tips and Tricks
Think 'robot mode' !
A crucial part of bubble sort is the last pass has no swaps
If you are not following the algorithm precisely, this pass can easily be missed out
Make it clear when you have completed the bubble sort algorithm, and state how you know it is complete
e.g. "there were no swaps in the fifth pass so the algorithm is complete and the list is in order"
e.g. (for 10 items) "that is the end of the
pass so the algorithm is complete and the list is in order"
After completing your solution, double-check whether a question required the list to be in ascending or descending order
If you've got it the wrong way round, there's no need to redo the question but
make it clear that after the algorithm is completed, you are reversing the list
make sure your final answer is in the order required by the question
Worked Example
The time, to the nearest second, taken by 7 participants to answer a general knowledge question are 5, 7, 4, 9, 3, 5, 6. The times are to be sorted into ascending order using the bubble sort algorithm.
a) Write down
i) the maximum number of passes the algorithm will require,
ii) the number of comparisons required for the third pass,
iii) the number of swaps there will be in the first pass.
i) The maximum number of passes is
The maximum number of passes will be 6
ii) The pass will have
comparisons
The number of comparisons required in the third pass will be 4
iii) Carefully do this by inspection (or you can carry out the first pass to be sure but that takes time)
The first swap will be the 7 and 4
The 9, being the highest value on the list, will then swap with each of the values that follow it (3 values)
The number of swaps in the first pass is 4
b) After the second pass of the bubble sort algorithm, the times are in the order 4, 5, 3, 5, 6, 7, 9.
Perform the third pass of the bubble sort algorithm and state the number of swaps made.
As this is the third pass, the last two items on the list, 7 and 9, will already be in the correct place The working list (that we apply a pass of the bubble sort algorithm to) will be 4, 5, 3, 5, 6
4 | 5 | 3 | 5 | 6 | 7 | 9 |
| 4 < 5, no swap |
4 | 5 | 3 | 5 | 6 | 7 | 9 |
| 5 > 3, swap |
4 | 3 | 5 | 5 | 6 | 7 | 9 |
| 5 = 5, no swap |
4 | 3 | 5 | 5 | 6 | 7 | 9 |
| 5 < 6, no swap |
4 | 3 | 5 | 5 | 6 | 7 | 9 |
| end of pass 3 |
Number of swaps: 1
c) Explain why two further passes of the bubble sort algorithm are required to ensure the list is in ascending order.
At this stage of the algorithm the answer should be able to be deduced by inspection of the current list
Using the answer to part b), the current list is 4, 3, 5, 5, 6, 7, 9
The next pass will involve one swap - the 4 and the 3
The pass after that will involve no swaps and so the algorithm will be complete and the list will be in order
Thus, two further passes are required
It is important to state that the algorithm is complete and the reason why
Quick sort
What is the quick sort algorithm?
The quick sort algorithm arranges items into either ascending or descending order
Items are usually values
but could be letters or words and similar
for questions given in context values will be measures such as weights, lengths, scores or times
How does the quick sort algorithm work?
Each pass of the quick sort algorithm works by splitting a sub-list of the items into two halves around a pivot
one half will be the sub-list of values that are less than the pivot
for ascending order this sub-list would come before the pivot
the other half will be the sub-list of values that are greater than the pivot
for ascending order this sub-list would come after the pivot
values that are equal to the pivot can be listed in either half
for consistency we suggest always listing items equal to the pivot in the half greater than the pivot
on both sides of the pivot values would be listed in the order they appeared in the original list
The quick sort algorithm is complete when every item on the (original) list has been designated as a pivot
Which item is the pivot in the quick sort algorithm?
The pivot is the middle value in a sub-list of the items, without reordering
If there are two items in the middle of a sub-list then either item can be taken as the pivot
for consistency we suggest always choosing the item in the upper position as the pivot
In the first pass, there will be one pivot - the middle item in the whole list
In the second pass, there could be two (new) pivots - one in the lower half/sub-list, one in the upper half/sub-list
The only time this would not be the case is when the pivot is the lowest (ascending) or greatest (descending) item on a sub-list
The number of pivots could double at each pass
How do I apply the quick sort algorithm?
The following list of steps describe the quick sort algorithm for arranging a list of items into ascending order
Arranging into descending order would be the same, but the 'ordering' in Step 2 would be reversed
STEP 1 Find and highlight the pivot (middle value) for each sub-list of items For the first pass only, the sub-list will be the same as the entire list of items
STEP 2 List items lower than the pivot, in the order they appear, before the pivot, creating a new (smaller) sub-list Then write the pivot as the next number on the list List items greater than or equal to the pivot, in the order they appear, after the pivot, creating another new (smaller) sub-list
STEP 3 Repeat steps 1 and 2 until every item on the original list has been designated a pivot The original (full) list of items will now be in ascending order
Examiner Tips and Tricks
Make it clear which items you have chosen as pivots at each pass of the quick sort algorithm
However, do not use different colours on the exam paper - they will not show up
(papers are usually scanned into marking systems in black and white)
use different styles instead such as
underlining values using solid, dotted, wavy, double, etc lines
drawing different shaped boxes (rectangle, circle, star, etc) around values
Worked Example
The following values are to be sorted into descending order using the quick sort algorithm.
5, 3, 7, 2, 4, 5, 9, 6
Clearly showing your choice of pivots at each pass, perform the quick sort algorithm to sort the list into descending order.
STEP 1
This is the first pass so the entire list will be the sub-listThere are 8 values so the pivot will be the 5th value on the list Pass 1 (pivot 4)
5 | 3 | 7 | 2 | 5 | 9 | 6 |
STEP 2
As descending order is required, list items greater than the pivot (4) before it; items lower than the pivot after it
5 | 7 | 5 | 9 | 6 | 3 | 2 |
STEP 3
The two sub-lists 5, 7, 5, 9, 6 and 3, 2 Repeat steps 1 and 2 on these sub-lists Pass 2 (pivots 5 and 2)
5 | 7 | 9 | 6 | 3 |
The (repeated) 5 will go into the 'greater than or equal to' sub-list (before the pivot 5 as descending)
There is no sub-list after the pivot 2 as it is the lowest value in its current sub-list
7 | 9 | 6 | 5 | 3 |
Continuing repeating steps 1 and 2 on each new sub-list until every item has been designated a pivot Pass 3 (pivots 6 and 3)
7 | 9 | 5 |
7 | 9 | 5 |
Notice that pass 3 did not involve any reordering but it is still crucial to show the pivots so that the algorithm has been precisely followed
Pass 4 (pivots 9 and 5)
7 |
7 |
Pass 5 (pivot 7)
Every value has now been designated as a pivot so the algorithm is complete and the list is in descending order
9, 7, 6, 5, 5, 4, 3, 2

Unlock more, it's free!
Did this page help you?