Simple Harmonic Motion (SHM) (DP IB Physics): Revision Note
Conditions for Simple Harmonic Motion
Simple harmonic motion (SHM) is a specific type of oscillation where:
There is repetitive movement back and forth through an equilibrium, or central, position, so the maximum horizontal or vertical displacement on one side of this position is equal to the maximum horizontal or vertical displacement on the other
The time interval of each complete vibration is the same (periodic)
The force responsible for the motion (restoring force) is always directed horizontally or vertically towards the equilibrium position and is directly proportional to the distance from it
Examples of SHM
Examples of oscillators that undergo SHM are:
The pendulum of a clock
A child on a swing
The vibrations of a bowl
A bungee jumper reaching the bottom of his fall
A mass on a spring
Guitar strings vibrating
A ruler vibrating off the end of a table
The electrons in alternating current flowing through a wire
The movement of a swing bridge when someone crosses
A marble dropped into a bowl
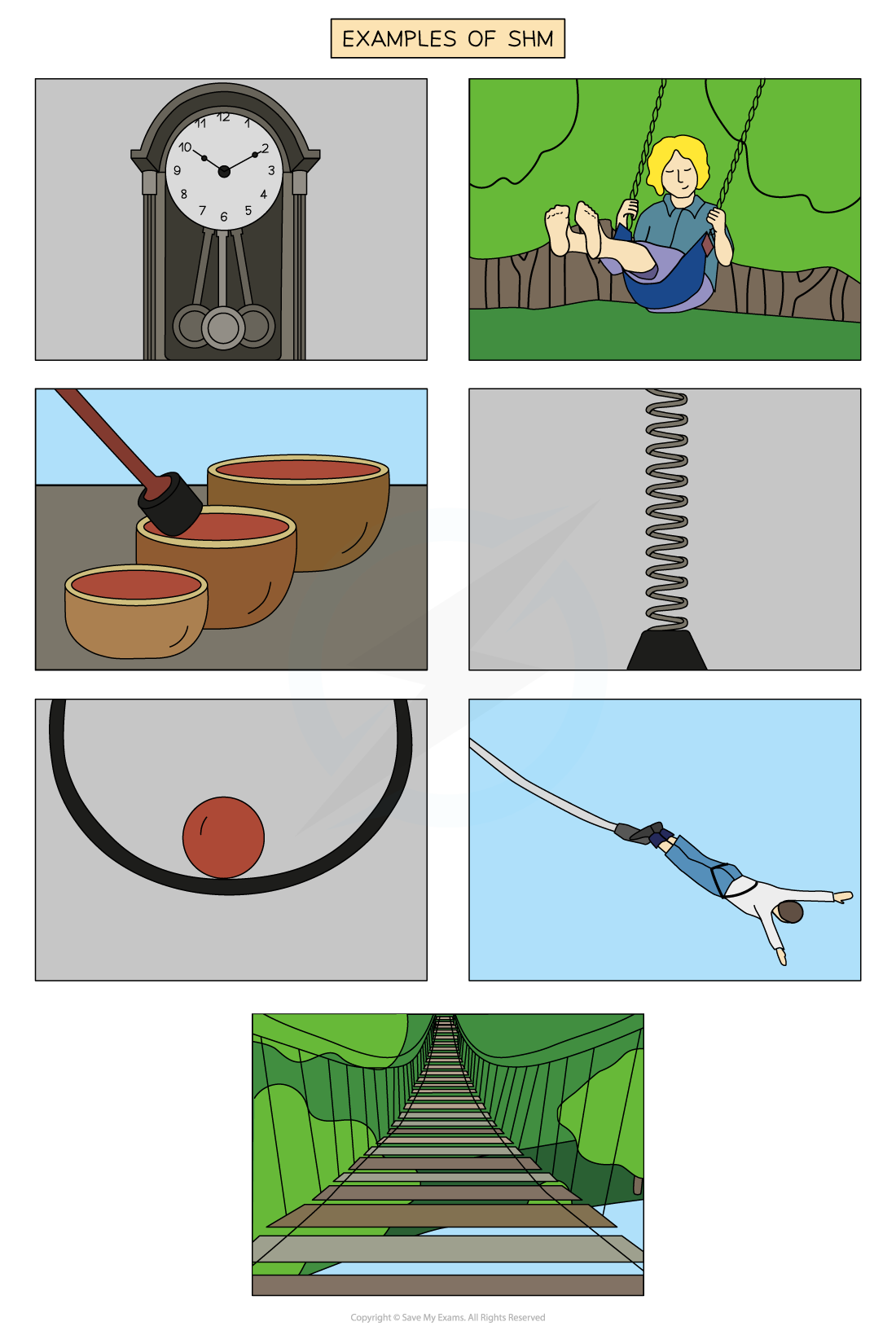
Examples of objects that undergo SHM
Modelling SHM
Not all oscillations are as simple as SHM
This is a particularly simple kind
It is relatively easy to analyse mathematically
Many other types of oscillatory motion can be broken down into a combination of SHMs
An oscillation is defined to be SHM when:
The acceleration is proportional to the horizontal or vertical displacement
The acceleration is in the opposite direction to the displacement (directed towards the equilibrium position)
The time period of oscillation is independent of the amplitude of the oscillation, for small angles of oscillation
So, for acceleration a and horizontal displacement x
a ∝ −x
You will be required to perform calculations on and explain two models of simple harmonic motion:
A simple pendulum oscillating from side to side attached to a fixed point above
A mass-spring system oscillating vertically up and down or horizontally back and forth
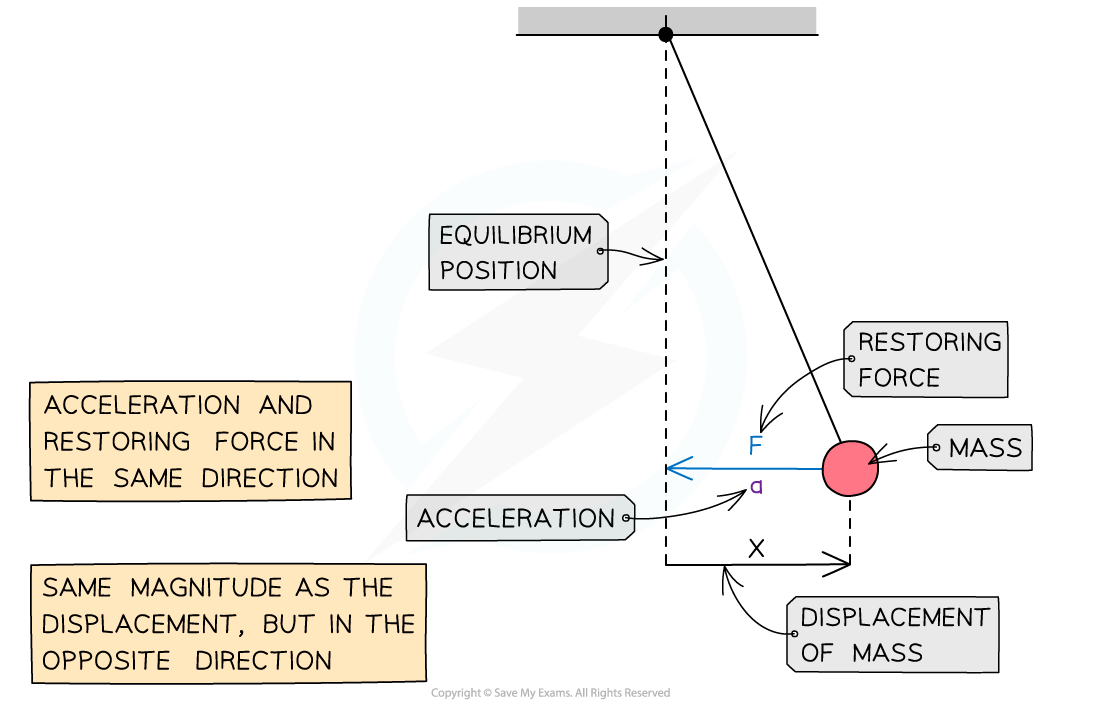
Force, acceleration and displacement of a simple pendulum in SHM

Force, acceleration and displacement of a mass-spring system in SHM
An Example of not SHM
A person jumping on a trampoline is not an example of simple harmonic motion because:
The restoring force on the person is not proportional to their displacement from the equilibrium position and always acts down
When the person is not in contact with the trampoline, the restoring force is equal to their weight, which is constant
This does not change, even if they jump higher
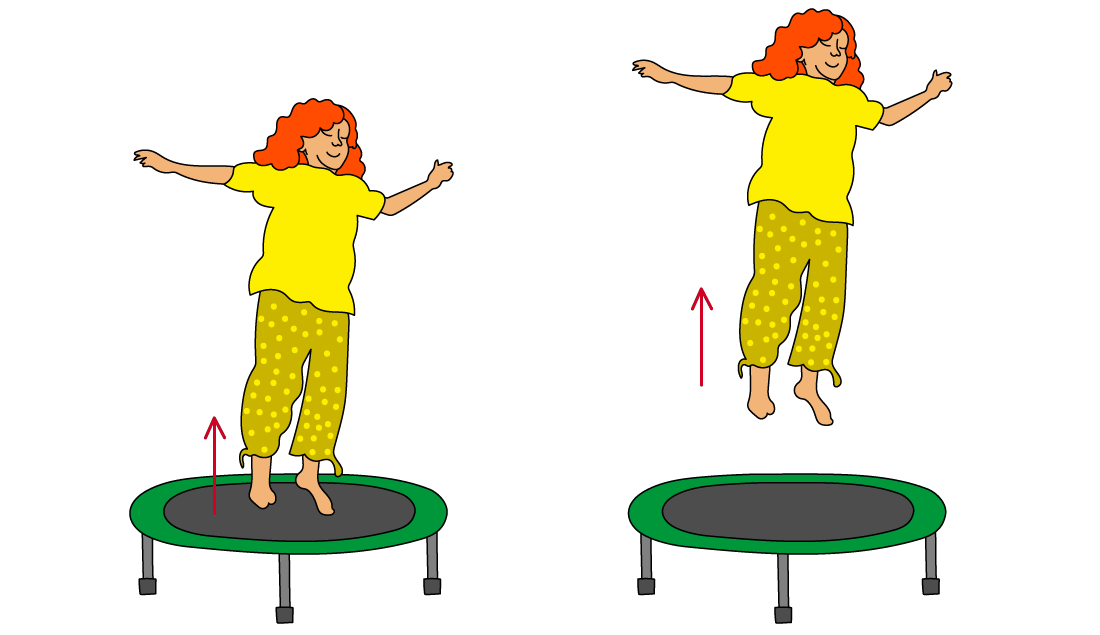
The restoring force of the person bouncing is equal to their weight and always acts downwards
Worked Example
Explain why a person jumping on a trampoline is not an example of simple harmonic motion.
Answer:
Step 1: Recall the conditions for simple harmonic motion
The conditions required for SHM:
The restoring force/acceleration is proportional to the displacement
The restoring force/acceleration is in the opposite direction to the displacement
Step 2: Consider the forces in the scenario given
When the person is not in contact with the trampoline, the restoring force is equal to their weight, which is constant
The value of their weight does not change, even if they jump higher (increase displacement)
Step 3: Write a concluding sentence
The restoring force on the person is not proportional to their distance from the equilibrium position, therefore, this scenario does not fulfil the conditions for SHM
The Defining Equation of Simple Harmonic Motion
The acceleration of an object oscillating in simple harmonic motion is given by the equation:
a = −⍵2x
Where:
a = acceleration (m s-2)
⍵ = angular frequency (rad s-1)
x = displacement (m)
The equation demonstrates:
Acceleration reaches its maximum value when the displacement is at a maximum, i.e. x = x0 at its amplitude
The minus sign shows that when the object is displaced to the right, the direction of the acceleration is to the left and vice versa (a and x are always in opposite directions to each other)
Consider the oscillation of a simple pendulum:
The bob accelerates as it moves towards the midpoint
Velocity is at a maximum when it passes through the equilibrium position
The pendulum slows down as it continues towards the other extreme of oscillation
v = 0 at xo as it changes direction
The pendulum then reverses and starts to accelerate again towards the midpoint
Graphical Representation of SHM
The displacement, velocity and acceleration of an object in simple harmonic motion can be represented by graphs against time
All undamped SHM graphs are represented by periodic functions
This means they can all be described by sine and cosine curves
You need to know what each graph looks like and how it relates to the other graphs
Remember that:
Velocity is the rate of change of displacement
Acceleration is the rate of change of velocity
Graphs that Start at the Equilibrium Position
When oscillations start from the equilibrium position:
the displacement-time graph is a sine curve
the velocity-time graph is the gradient of the displacement-time graph, so a cosine graph and 90° out of phase with the displacement-time graph
the acceleration-time graph is the gradient of the velocity-time graph, so a negative sine graph and 90° out of phase with the velocity-time graph
More information on this can be found in the IB DP Maths Differentiating Special Functions on trigonometric differentiation
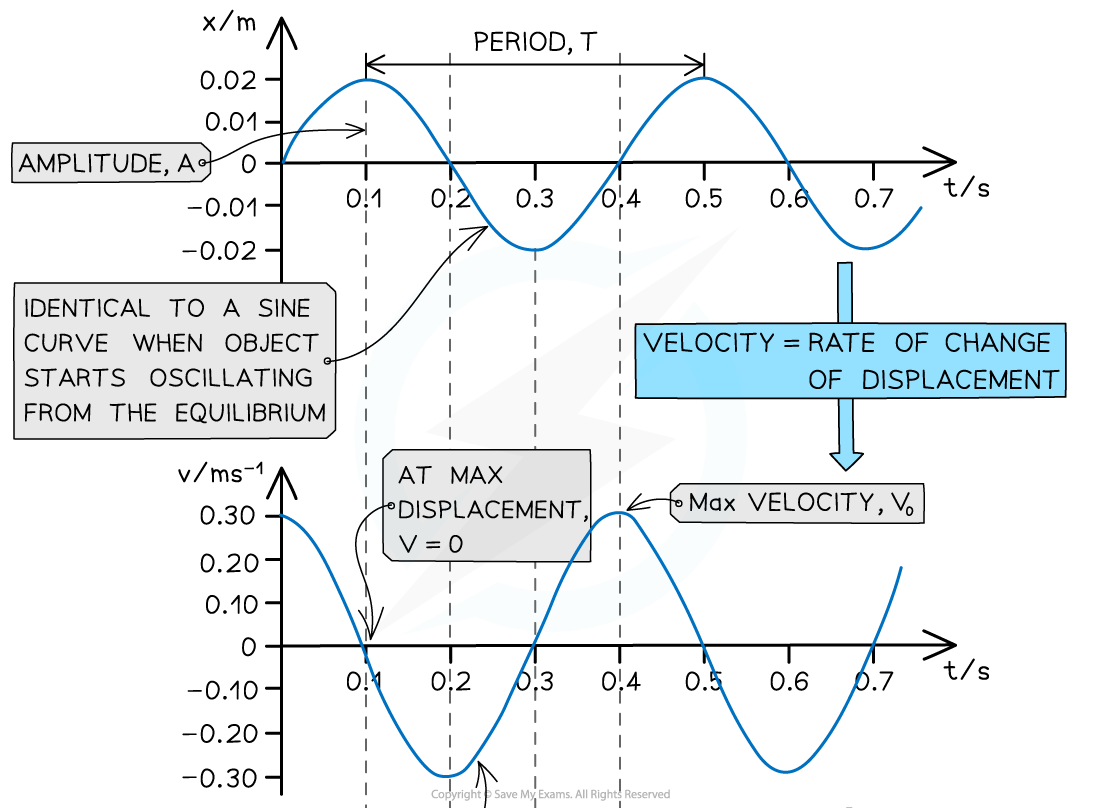
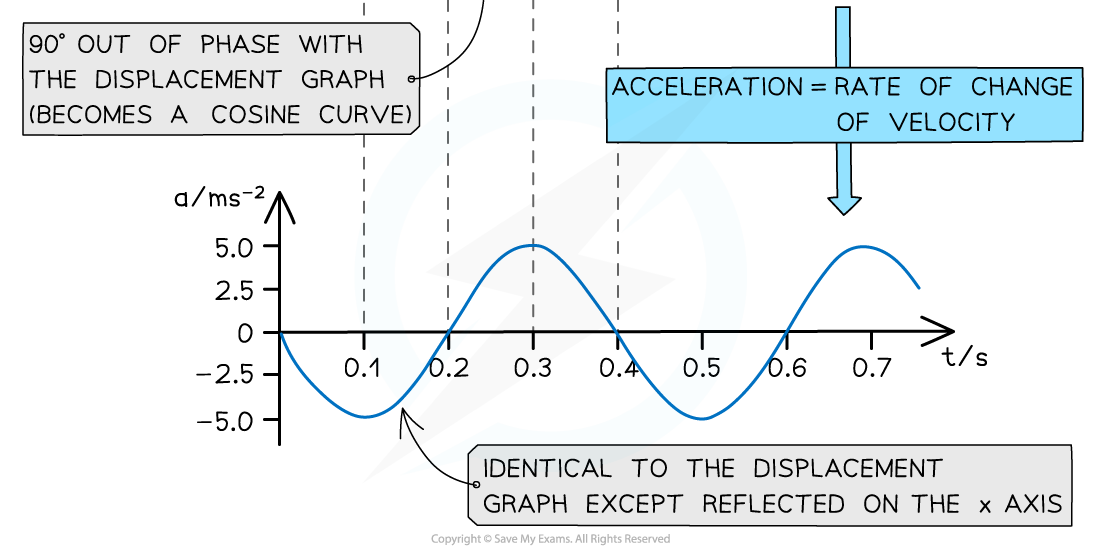
The displacement, velocity and acceleration graphs in SHM are all 90° out of phase with each other
Graphs that Start at the Amplitude Position
When oscillations start from the amplitude position:
the displacement-time graph is a cosine curve
the velocity-time graph is the gradient of the displacement-time graph, so a negative sine graph and 90° out of phase with the displacement-time graph
the acceleration-time graph is the gradient of the velocity-time graph, so a negative cosine graph and 90° out of phase with the velocity-time graph
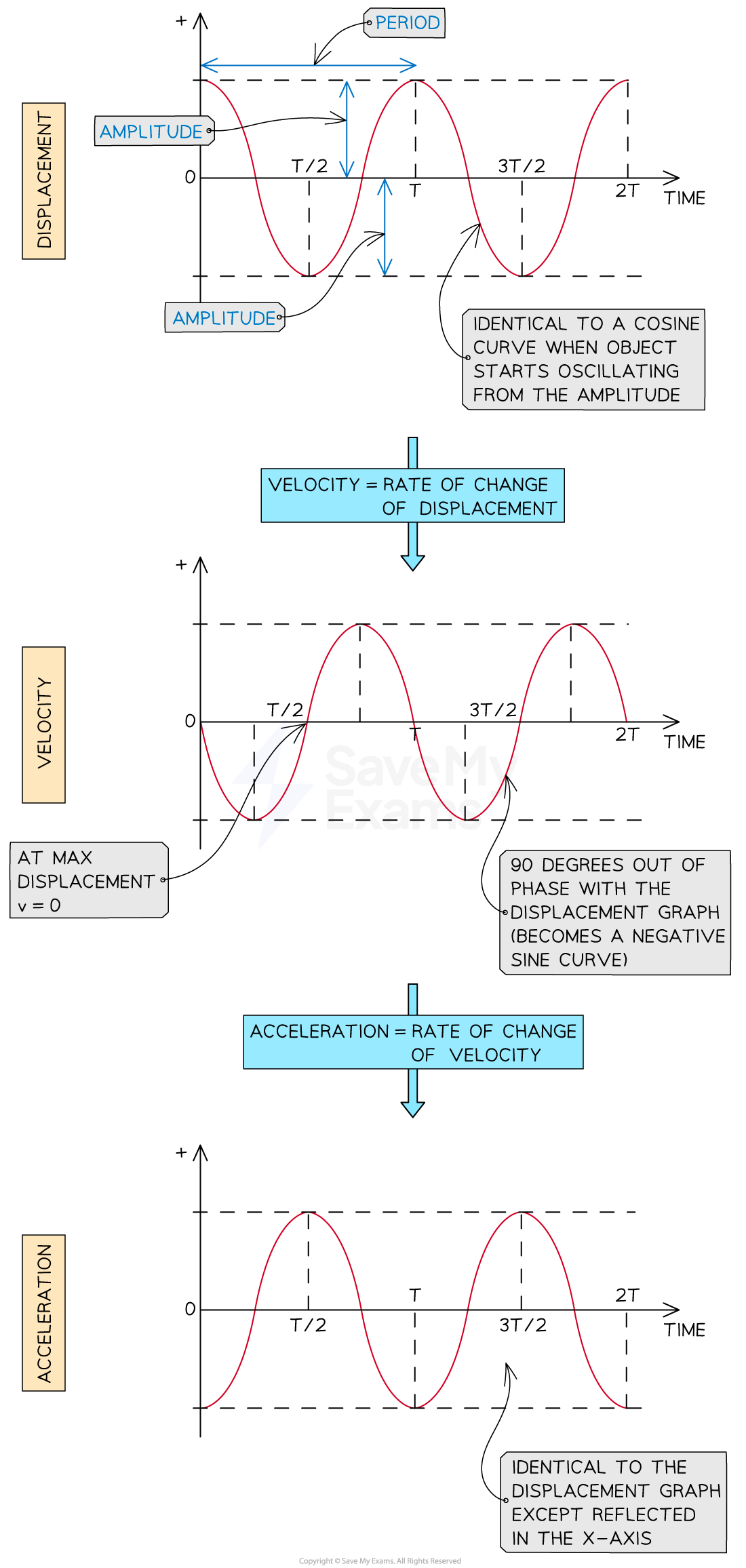
The displacement, velocity and acceleration graphs in SHM are all 90° out of phase with each other
Relationship Between Graphs
Key features of the displacement-time graphs:
The amplitude of oscillations A is the maximum value of x
The time period of oscillations T is the time taken for one full wavelength cycle
Key features of the velocity-time graphs:
The velocity of an oscillator at any time can be determined from the gradient of the displacement-time graph:

Key features of the acceleration-time graph:
The acceleration graph is a reflection of the displacement graph on the x-axis
This means when a mass has positive displacement (to the right), the acceleration is in the opposite direction (to the left) and vice versa (from a = −ω2x)
The acceleration of an oscillator at any time can be determined from the gradient of the velocity-time graph:

Worked Example
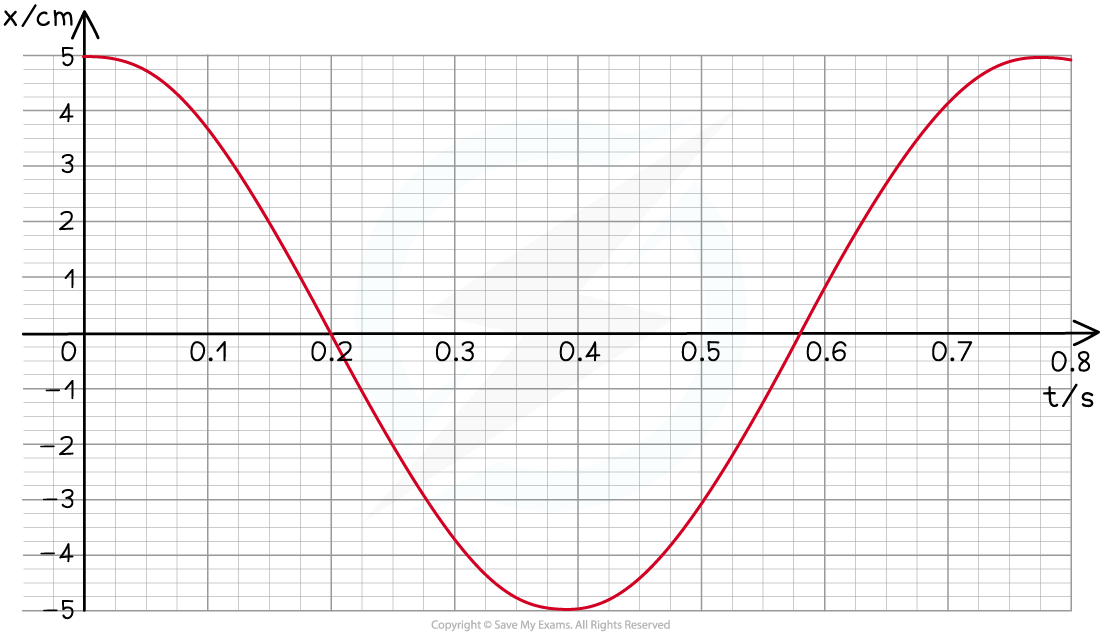
The swing exhibits simple harmonic motion.
Use data from the graph to determine at what time the velocity of the swing is first at its maximum.
Answer:
Step 1: The velocity is at its maximum when the displacement x = 0
Step 2: Reading value of time when x = 0
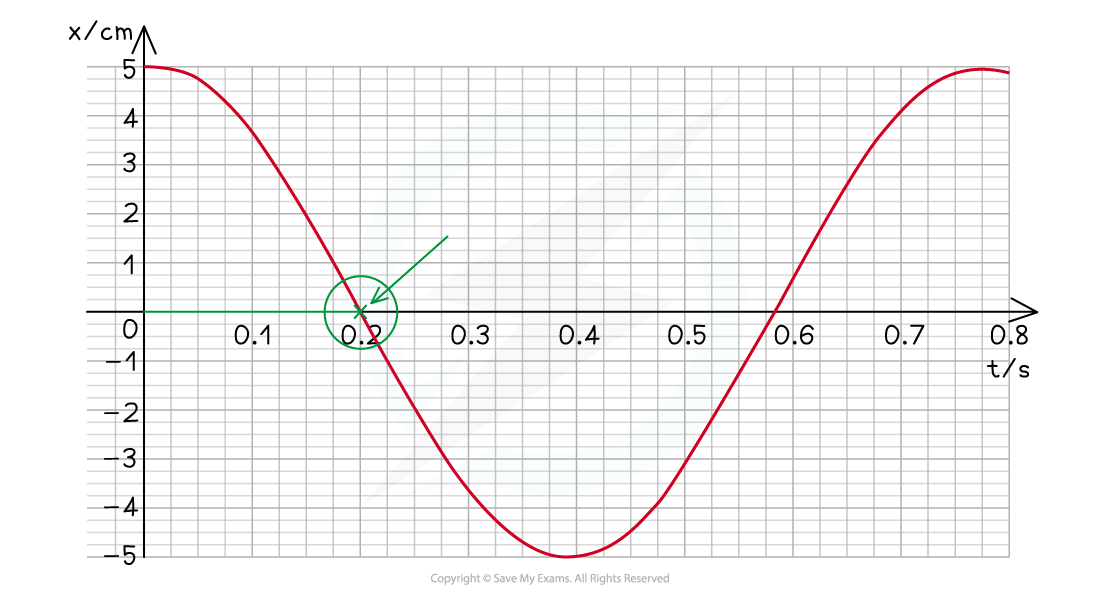
From the graph, this is equal to 0.2 s
Examiner Tips and Tricks
The defining equation of SHM shows acceleration, as a positive value, and displacement, −x as a negative one. This reminds us that acceleration and displacement are vector quantities and are always in the opposite direction to each other in SHM.
Since displacement is a vector quantity, remember to keep the minus sign in your solutions if they are negative. Getting the marks will depend on keeping your positive and negative numbers distinct from each other! Also remember that your calculator must be in radians mode when using the cosine and sine functions. This is because the angular frequency ⍵ is calculated in rad s-1, not degrees.
These graphs might not look identical to what is in your textbook, because they depend on the starting position of the oscillation of the object when t = 0. If there is no damping, they will be a sine or cosine curve.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?