Exponential Functions (Edexcel IGCSE Further Pure Maths)

Revision Note

Written by: Paul

Reviewed by: Dan Finlay

Exponential Functions & Graphs

What is an exponential function?

An exponential function is of the form $f (x) = a^{x}, a > 0$
Its domain is the set of all real numbers
Its range is the set of all positive real numbers
An important exponential function is $f (x) = e^{x}$
- e is the mathematical constant $2.718281 \dots$
- See the following note on " $e$ " for more details

What are the key features of exponential graphs?

The graphs have a $y$ -intercept at $(0, 1)$
- Because $a^{0} = 1$
The graph will always pass through the point $(1, a)$
- Because $a^{1} = a$
The graphs do not intersect the $x$ -axis
- The graphs have a horizontal asymptote at the x-axis $y = 0$
The graphs do not have any minimum or maximum points

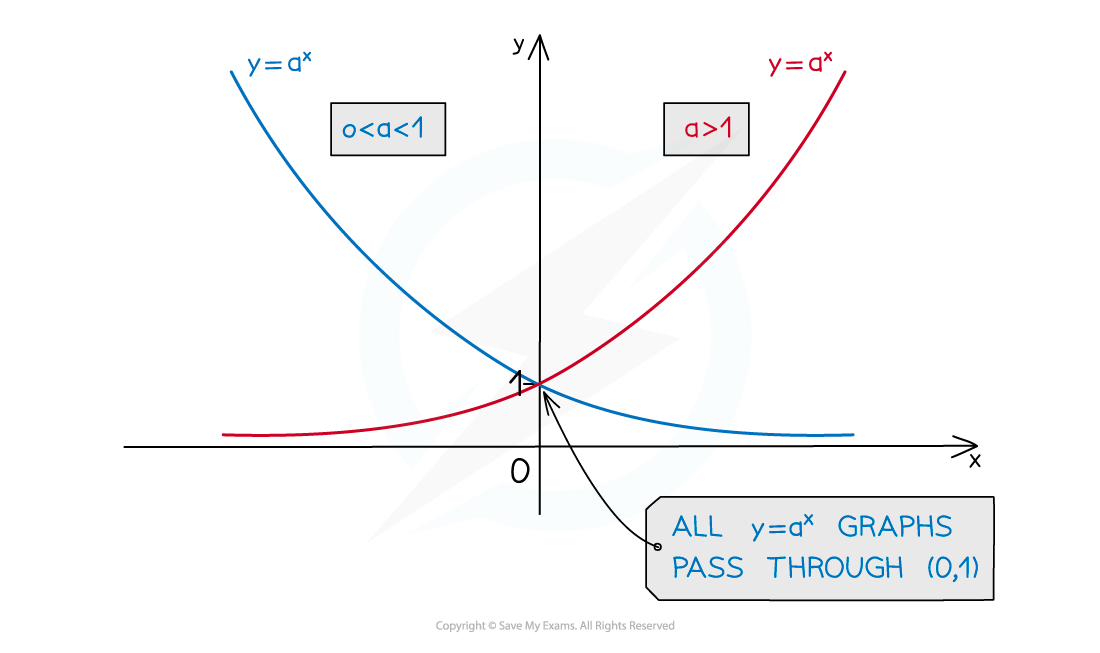
When $a > 1$
- For $x < 0$ the higher value of $a$ is the “lower” graph
- Where $x > 0$ the higher value of $a$ is the “higher” graph
When $0 < a < 1$
- Where $x < 0$ the higher value of $a$ is the “lower” graph
- Where $x > 0$ the higher value of $a$ is the “higher” graph
When $a = 1$
- The graph is a horizontal line through $y = 1$
- Because $1^{x} = 1$ for all values of $x$

Worked Example

On the same set of axes, sketch the graphs of $y = 3^{x}$ and $y = 4^{x}$ .

Both graphs will have the 'typical' $y = a^{x}$ exponential shape for the $a > 1$ case

$y = 4^{x}$ will be the 'lower' graph for $x < 0$ ,and the 'higher' graph for $x > 0$

Both graphs go through $(0, 1)$ and have an asymptote at the $x$ -axis

"e"

What is e, the exponential constant?

$e$ is one of the most important mathematical constants
- $e = 2.718281 . . .$
- $e$ is an irrational number
- $f (x) = e^{x}$ is often referred to as 'the exponential function'
As with other exponential graphs, $y = e^{x}$
- passes through $(0, 1)$
- has the $x$ -axis as an asymptote

Why is e so important?

$y = e^{x}$ has the particular property that $\frac{d y}{d x} = e^{x}$
- i.e. if $f (x) = e^{x}$ , then $f^{'} (x)$ is also equal to $e^{x}$
This means that for every real number $x$ , the gradient of $y = e^{x}$ is also equal to $e^{x}$

e Notes fig2, A Level & AS Maths: Pure revision notes

e Notes fig3, A Level & AS Maths: Pure revision notes

The negative exponential graph

$y = e^{- x}$ is a reflection in the $y$ -axis of $y = e^{x}$
- Note by laws of indices that $e^{- x} = {(e^{- 1})}^{x} = {(\frac{1}{e})}^{x}$
They are of the form $y = f (x)$ and $y = f (- x)$

Worked Example

On the same set of axes, sketch the graphs of $y = e^{x}$ , $y = e^{2 x}$ and $y = e^{- 2 x}$ .

By laws of indices, $e^{2 x} = {(e^{2})}^{x}$

$e^{2} > e$ , so $y = e^{2 x}$ will be the 'lower' graph for $x < 0$ ,and the 'higher' graph for $x > 0$

$y = e^{- 2 x}$ is the reflection of $y = e^{2 x}$ in the $y$ -axis

All three graphs go through $(0, 1)$ and have an asymptote at the $x$ -axis

Last updated: 16 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Next:Logarithmic Functions

Exponential Functions (Edexcel IGCSE Further Pure Maths)

Revision Note

Exponential Functions & Graphs

What is an exponential function?

What are the key features of exponential graphs?

Worked Example

"e"

What is e, the exponential constant?

Why is e so important?

The negative exponential graph

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Paul

Author: Dan Finlay