Logarithmic Functions (Edexcel IGCSE Further Pure Maths): Revision Note

Written by: Amber

Reviewed by: Dan Finlay

Updated on 16 October 2024

Introduction to Logarithms

What are logarithms?

A logarithm is the inverse of an exponent
- If $a^{x} = b$ then $\log_{a} (b) = x$ , where $a > 0, b > 0, a \neq 1$
  - This is the essential definition of a logarithm
  - The number $a$ is called the base of the logarithm

Try to get used to ‘reading’ logarithm statements to yourself
- $\log_{a} (b) = x$ means “ $x$ is the power that you raise $a$ to, to get $b$ "
- So $\log_{5} 125 = 3$ means “3 is the power that you raise 5 to, to get 125”

Two important special cases are:
- $\ln x = \log_{e} (x)$
  - Where $e$ is the mathematical constant 2.718…
  - This is called the natural logarithm and will have its own button on your calculator
- $\log x = \log_{10} (x)$
  - Logarithms of base 10 are frequently used
  - They are often abbreviated simply as $\log x$

Why use logarithms?

Logarithms allow us to solve equations where the exponent is the unknown value
- We can solve some of these by inspection
  - For example, for the equation $2^{x} = 8$ we know that $x$ must be $3$
- But logarithms allow us to solve more complicated problems
  - For example, the equation $2^{x} = 10$ does not have an obvious answer
  - Instead we can rewrite the equation as a logarithm

$\log_{2} 10 = x$

and use our calculator to find the decimal value of $\log_{2} 10$

$x = 3.321928 . . .$

Examiner Tips and Tricks

Make sure you are completely familiar with your calculator's logarithm functions

Worked Example

Solve the following equations:

i) $x = \log_{3} 27$ ,
Use the definition of a logarithm to rewrite this as an exponential equation

Remember, this equation means " $x$ is the power that you raise 3 to, to get 27"

$3^{x} = 27$

This can be solved by inspection

$3^{3} = 27$

$x = 3$

ii) $2^{x} = 21.4$ , giving your answer to 3 s.f.

Use the definition of a logarithm to rewrite this as a logarithm equation

We want the logarithm that means " $x$ is the power that you raise 2 to, to get 21.4"

$x = \log_{2} 21.4$

Use your calculator to find the value of that logarithm

$x = 4.419538 . . .$

Round to 3 significant figures

$x = 4.42$ (3 s.f.)

Logarithmic Functions & Graphs

What is a logarithmic function?

A logarithmic function is of the form $f (x) = \log_{a} x, x > 0$
- In this course the base $a$ for a logarithmic function will always be an integer greater than one
Its domain is the set of all positive real numbers
- You can't take a log of zero or a negative number
Its range is the set of all real numbers
$\log_{a} x$ and $a^{x}$ are inverse functions
- $\log_{a} (a^{x}) = x$ and $a^{\log_{a} x} = x$

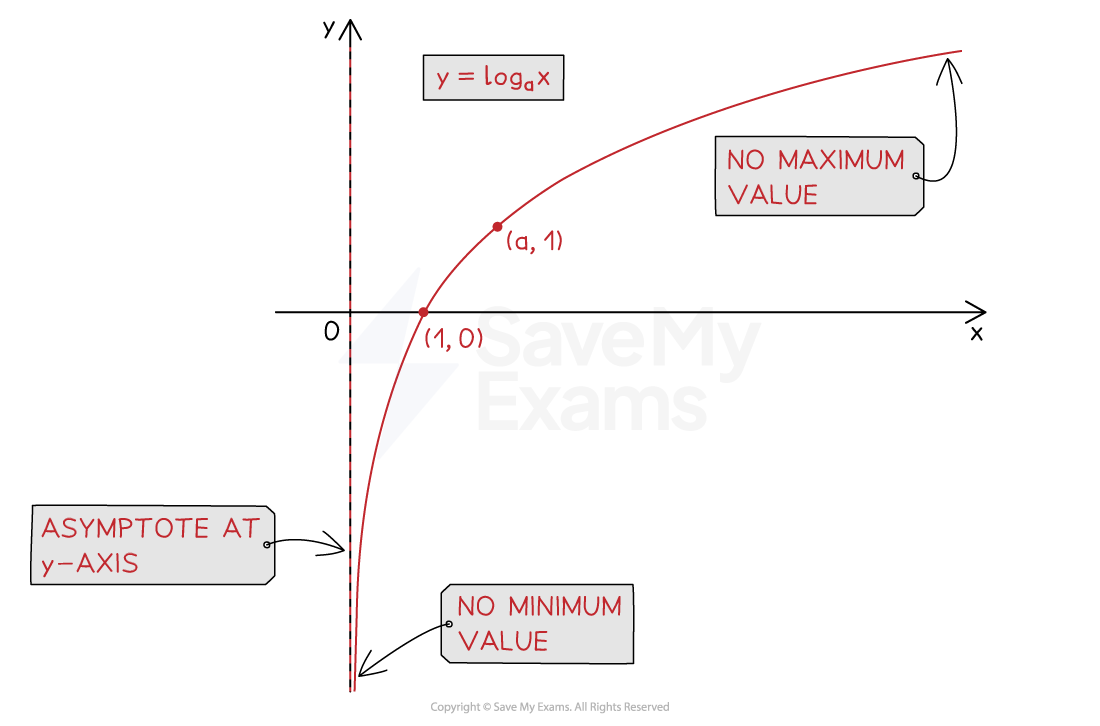
What are the key features of logarithmic graphs?

The graph of $y = \log_{a} x$
- does not have a $y$ -intercept
- has a vertical asymptote at the y-axis: $x = 0$
- has one $x$ -intercept at (1, 0)
- passes through the point (a, 1)
- does not have any minimum or maximum points

Worked Example

On the same set of axes, sketch the graphs of $y = \log_{3} x$ and $y = 3^{x}$ . Be sure to label any axis intercepts.

$y = \log_{3} x$ will have the typical logarithmic graph shape
The $y$ -axis is an asymptote, and the $x$ -intercept is $(1, 0)$

$y = 3^{x}$ will have the typical exponential graph shape
The $x$ -axis is an asymptote, and the $y$ -intercept is $(0, 1)$

$\log_{3} x$ and $3^{x}$ are inverse functions
Therefore their graphs will be reflections of each other in the line $y = x$

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.
Beth
IGCSE Student
This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!
Fathima
A Level Student
Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.
Kate
GCSE Student
Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.
Sameera
Parent
Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years
Mark
Chemistry Teacher
Excellent
Read more reviews

Did this page help you?

Previous:Exponential FunctionsNext:Properties of Indices

Logarithms, Indices & Surds

Logarithms, Indices & Exponentials

Exponential Functions

Logarithmic Functions

Properties of Indices

Properties of Logarithms

Solving Exponential Equations

Surds

Simplifying Surds

Rationalising Denominators

Equations, Identities & Inequalities

Quadratic Functions

Factorising Quadratics

Completing the Square

Solving Quadratic Equations

Roots of Quadratic Equations

Equations & Identities

Algebraic Division

Factor & Remainder Theorems

Solving Cubic Equations

Simultaneous Equations

Inequalities

Solving Inequalities

Graphs of Inequalities

Coordinate Geometry & Graphs

Coordinate Geometry

Basic Coordinate Geometry

Equations of a Straight Line

Graphs

Graphing Functions

Graphs of Polynomials

Graphs of Rational Functions

Solving Equations Graphically

Series

Arithmetic & Geometric Series

Sigma Notation

Arithmetic Sequences & Series

Geometric Sequences & Series

Binomial Series

Binomial Expansion

General Binomial Expansion

Applications of Binomial Expansion

Geometry & Trigonometry

Radians

Radian Measure

Arcs & Sectors

Trigonometric Ratios

Basic Trigonometry

Sin, Cos & Tan

Graphs of Trigonometric Functions

Trigonometric Formulae & Identities

Sine & Cosine Formulae

Trigonometric Identities

Trigonometric Addition Formulae

Trigonometric Equations

Linear Trigonometric Equations

Quadratic Trigonometric Equations

Vectors

Vectors

Vector Basics

Position & Displacement Vectors

Magnitude of a Vector

Geometric Proof with Vectors

Calculus

Differentiation

Introduction to Derivatives

Differentiating Basic Functions

Techniques of Differentiation

Applications of Differentiation

Finding Gradients

Stationary Points & Turning Points

Tangents & Normals

Rates of Change

Integration

Introduction to Integration

Integrating Basic Functions

Constants of Integration

Applications of Integration

Calculating Areas

Areas Between Curves