Graphs of Polynomials (Edexcel IGCSE Further Pure Maths)

Revision Note

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Quadratic Functions & Graphs

What are the key features of quadratic graphs?

A quadratic graph can be written in the form $y = a x^{2} + b x + c$ where $a \neq 0$
The shape of the graph is known as a parabola
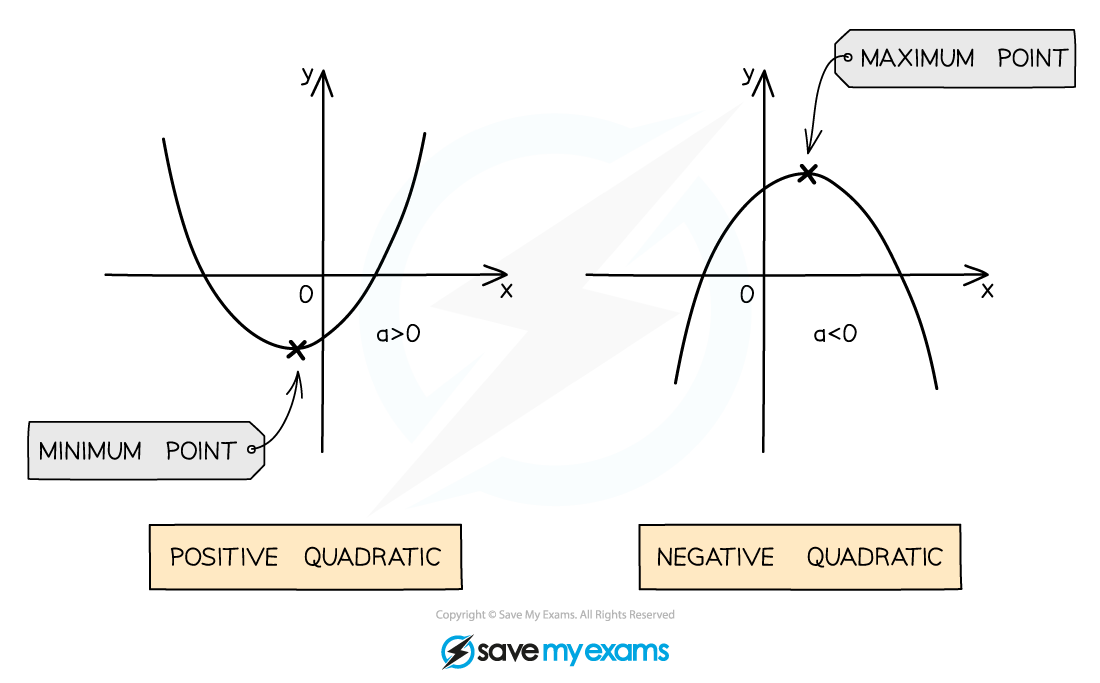
The value of a affects the shape of the curve
- If a is positive the shape is 'u-shaped' ∪
- If a is negative the shape is 'upside down u-shaped' ∩
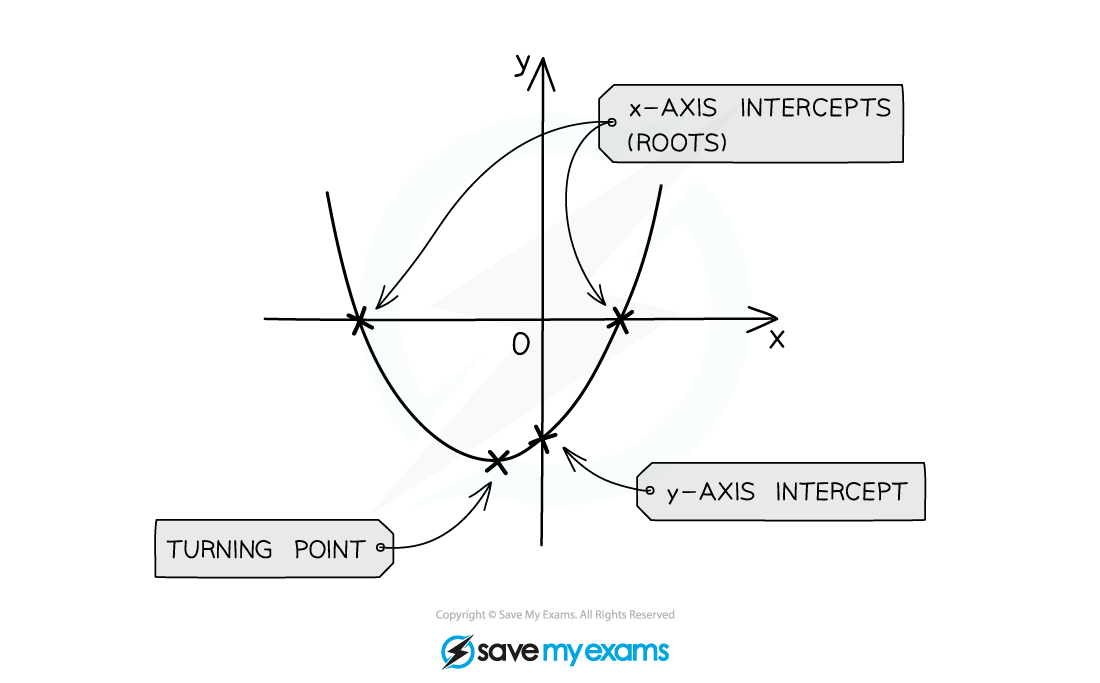
The y-intercept is at the point (0, c)
The roots are the solutions to $a x^{2} + b x + c = 0$
- These are also known as the x-intercepts or zeroes
- They can be found by
  - Factorising
  - Quadratic formula
  - Completing the square
  - Your calculator may also be able to find these for you
- There can be 0, 1 or 2 x-intercepts
  - This is determined by the value of the discriminant
There is an axis of symmetry at $x = - \frac{b}{2 a}$
- If there are two x-intercepts then the axis of symmetry goes through the midpoint between them
The vertex lies on the axis of symmetry
- It can be found by completing the square
- The x-coordinate is $x = - \frac{b}{2 a}$
- The y-coordinate can be found by calculating y when $x = - \frac{b}{2 a}$
- If a is positive then the vertex is the minimum point
- If a is negative then the vertex is the maximum point

What are the equations of a quadratic function?

$f (x) = a x^{2} + b x + c$
- This is the general form
- It clearly shows the y-intercept (0, c)
- You can find the axis of symmetry by $x = - \frac{b}{2 a}$
$f (x) = a (x - p) (x - q)$
- This is the factorised form
- It clearly shows the roots (p, 0) & (q, 0)
- You can find the axis of symmetry by $x = \frac{p + q}{2}$
$f (x) = a {(x - h)}^{2} + k$
- This is the vertex form (or completed square form)
- It clearly shows the vertex (h, k)
- The axis of symmetry is therefore $x = h$
- It clearly shows how the function can be transformed from the graph of $y = x^{2}$
  - Vertical stretch by scale factor a
  - Translation by vector $(\begin{matrix} h \\ k \end{matrix})$

How do I find an equation of a quadratic?

If you have the roots x = p and x = q...
- Write in factorised form $y = a (x - p) (x - q)$
- You will need a third point to find the value of a
If you have the vertex (h, k) then...
- Write in vertex form $y = a {(x - h)}^{2} + k$
- You will need a second point to find the value of a
If you have three random points (x₁, y₁), (x₂, y₂) & (x₃, y₃) then...
- Write in the general form $y = a x^{2} + b x + c$
- Substitute the three points into the equation
- Form and solve a system of three linear equations to find the values of a, b & c

Examiner Tips and Tricks

Your calculator may be able to find the roots and turning point of a quadratic function
- Even on a 'show that' question this can be used to check your answers

Worked Example

The diagram below shows the graph of $y = f (x)$ , where $f (x)$ is a quadratic function.

The vertex and the intercept with the $y$ -axis have been labelled.

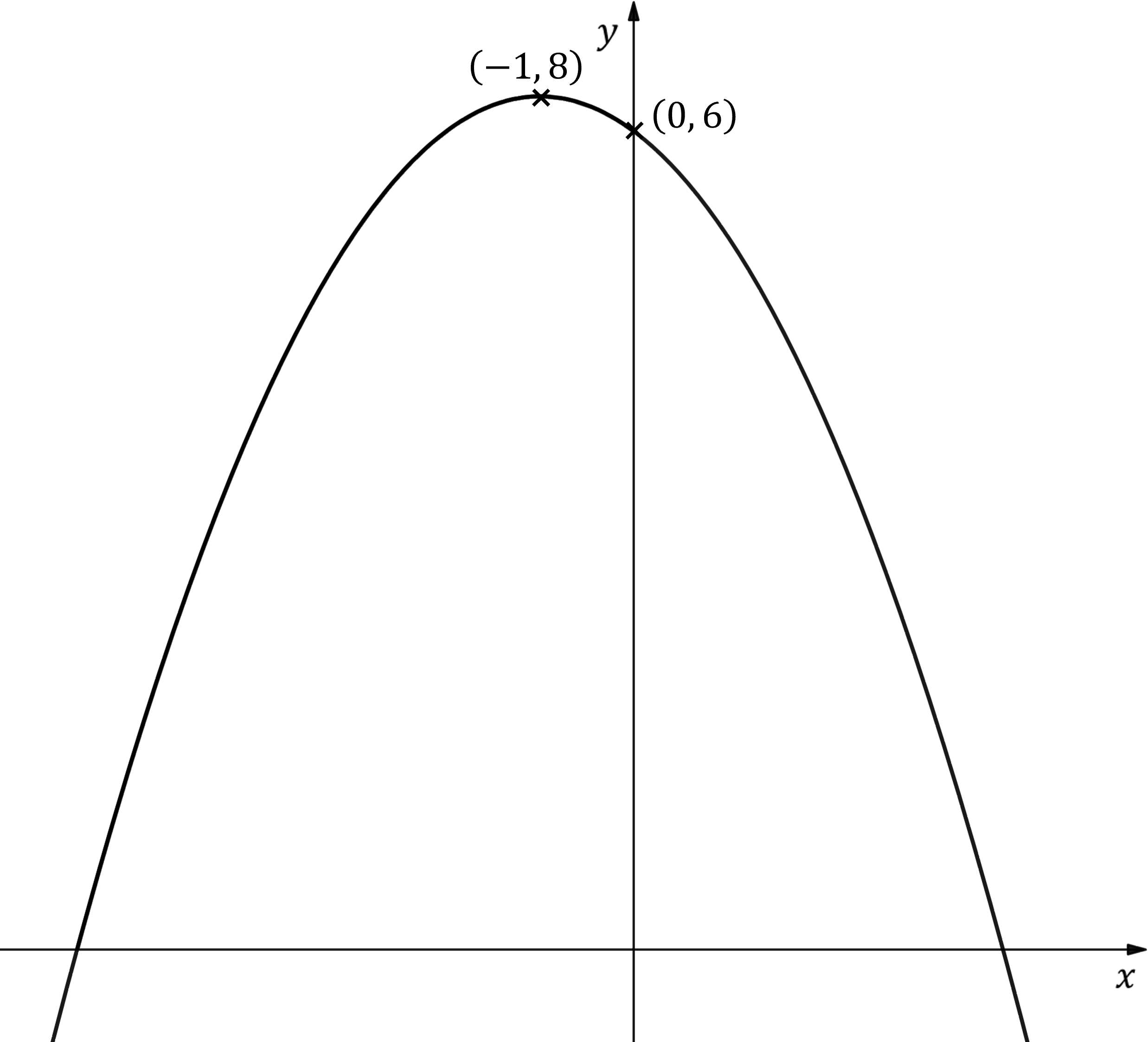
Find an expression for $y = f (x)$ .

Method 1

Since we know the vertex (turning point), it will be easiest to start with the completed square version of the equation
This is $f (x) = a {(x - h)}^{2} + k$ , where the vertex is at $(h, k)$

$\begin{array}{rcl} f (x) & = & a {(x - (- 1))}^{2} + 8 \\ = & a {(x + 1)}^{2} + 8 \end{array}$

We also know the curve $y = f (x)$ goes through (0, 6)
Put those coordinates into the equation and solve for $a$

$\begin{array}{rcl} 6 & = & a {(0 + 1)}^{2} + 8 \\ 6 & = & a + 8 \\ a & = & - 2 \end{array}$

Substitute $a = - 2$ into the expression for $f (x)$
Expand the brackets and rearrange into the form required

$\begin{array}{rcl} f (x) & = & - 2 {(x + 1)}^{2} + 8 \\ = & - 2 (x^{2} + 2 x + 1) + 8 \\ = & - 2 x^{2} - 4 x - 2 + 8 \end{array}$

$f (x) = - 2 x^{2} - 4 x + 6$

Method 2

It is also possible to start with the $y = a x^{2} + b x + c$ form
Because the y-intercept is (0, 6) we know that $c = 6$

Goes through $(0, 6)$ means $f (x) = a x^{2} + b x + 6$

It also goes through (-1, 8)
Substitute those coordinates into the equation of $y = f (x)$

Goes through $(- 1, 8)$ means

$\begin{array}{rcl} 8 & = & a {(- 1)}^{2} + b (- 1) + 6 \\ 8 & = & a - b + 6 \\ a - b & = & 2 \end{array}$

We need one more piece of information
You may remember that the turning point lies on the line $x = - \frac{b}{2 a}$
If not, then use the fact that the x-coordinate of the turning point satisfies $f^{'} (x) = 0$

Turning point at $(- 1, 8)$ means $f^{'} (- 1) = 0$

Differentiate to find $f^{'} (x)$
Then solve $f^{'} (- 1) = 0$ to find another equation with $a$ and $b$

$f^{'} (x) = 2 a x + b$

$\begin{array}{rcl} 2 a (- 1) + b & = & 0 \\ - 2 a + b & = & 0 \end{array}$

We now have two simultaneous equations that we can solve to find $a$ and $b$

$\begin{array}{rcl} a - b & = & 2 [1] \\ - 2 a + b & = & 0 [2] \end{array}$

Add [1] and [2] together to eliminate $b$

$\begin{array}{rcl} - a & = & 2 \\ a & = & - 2 \end{array}$

Substitute into [2] and solve to find $b$

$\begin{array}{rcl} - 2 (- 2) + b & = & 0 \\ 4 + b & = & 0 \\ b & = & - 4 \end{array}$

Write final answer in form requested

$f (x) = - 2 x^{2} - 4 x + 6$

Cubic Functions & Graphs

What are the key features of cubic graphs?

A cubic graph can be written in the form $y = a x^{3} + b x^{2} + c x + d$ where $a \neq 0$
When asked to consider the equation of a cubic and its graph, think about the following
- y-axis intercept
  - This occurs at $(0, d)$
- x-axis intercepts (roots)
  - x-coordinates are the solutions to $a x^{3} + b x^{2} + c x + d = 0$
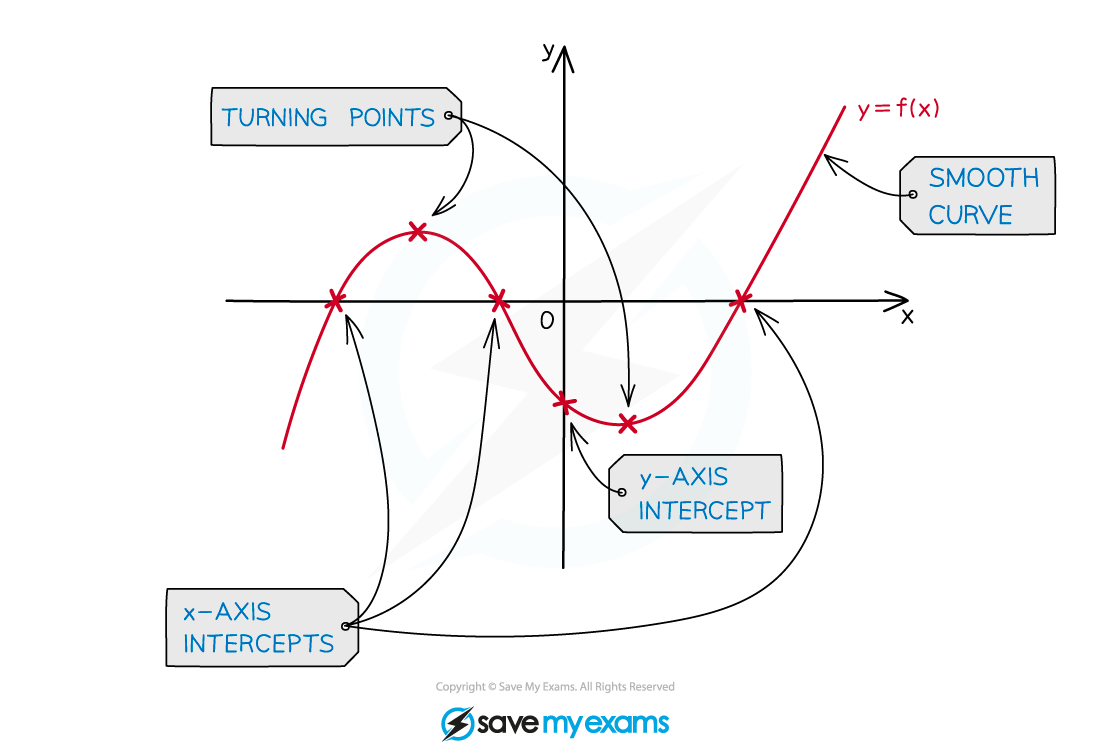
- turning points (maximum and/or minimum)
  - A cubic can have 0, 1 or 2 turning points
  - x-coordinates are the solutions to $3 a x^{2} + 2 b x + c = 0$
  - these are when the derivative of $a x^{3} + b x^{2} + c x + d$ equals 0
- The value of $a$ affects the shape of the curve
  - If $a$ is positive the ends of the curve will go 'down on the left and up on the right'
  - If $a$ is negative the ends of the curve will go 'up on the left and down on the right'

How do I sketch the graph of a cubic?

STEP 1
Find the y-axis intercept by setting x = 0
STEP 2
Find the x-axis intercepts (roots) by setting y = 0
- This may require factorising the cubic
STEP 3
Consider the shape and “start”/”end” of the graph
- a positive cubic graph starts in third quadrant (“bottom left”) and ends in first quadrant (“top right”)
- a negative cubic graph starts in second quadrant (“top left”) and ends in fourth quadrant (“bottom right”)
STEP 4
Consider where any turning points should go
- Differentiate the equation of the curve and set equal to zero
STEP 5
Draw with a smooth curve (this takes practice!)

Worked Example

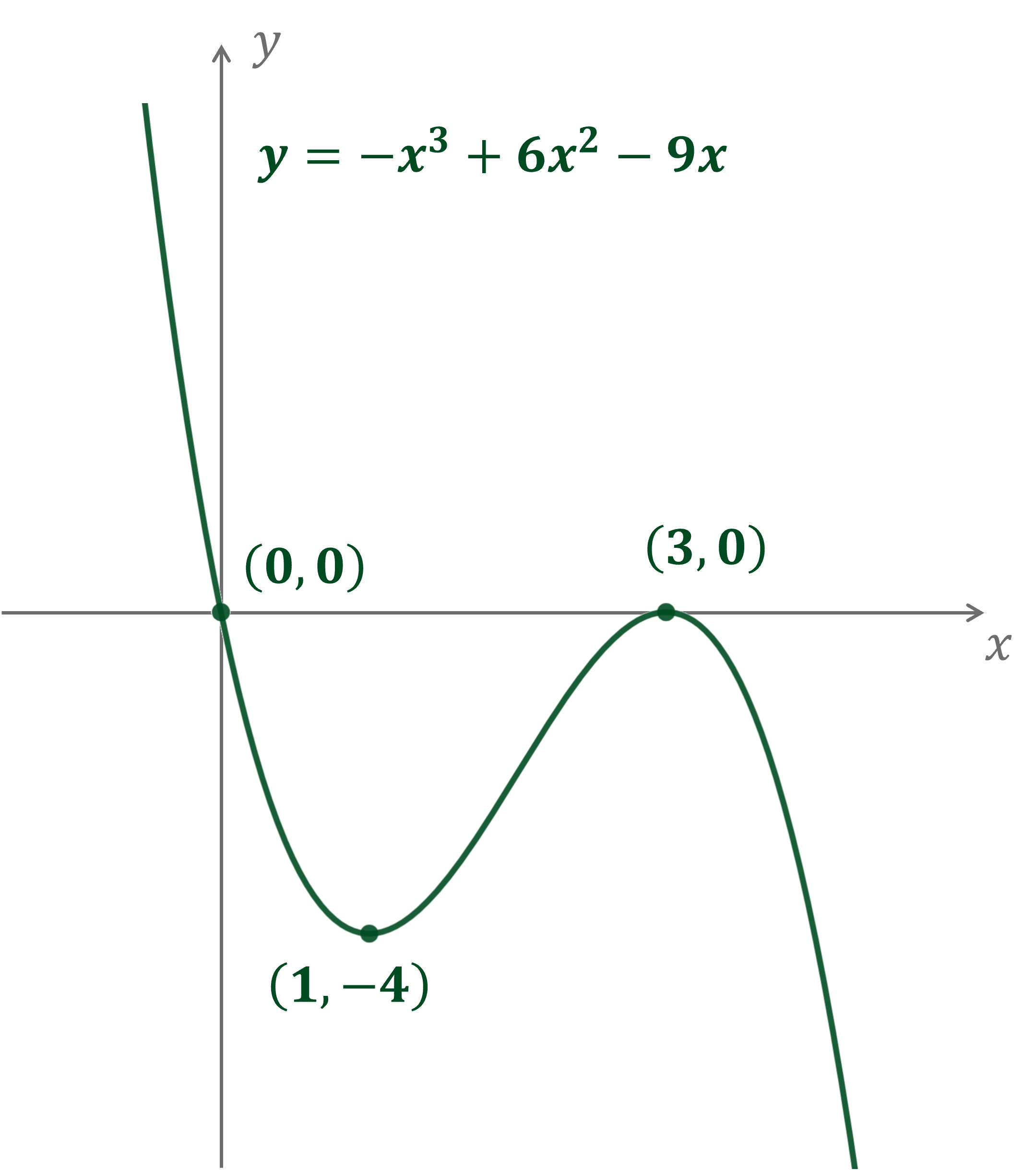
Consider the function $f (x) = - x^{3} + b x^{2} + c x$ , where $b$ and $c$ are constants.

The graph of $y = f (x)$ has two turning points, the $x$ -coordinates of which are $1$ and $3$ .

(a) Find the values of $b$ and $c$ .

The turning points occur when $f^{'} (x) = 0$

Start by differentiating to find $f^{'} (x)$

$f^{'} (x) = - 3 x^{2} + 2 b x + c$

That is equal to 0 when $x = 1$ and when $x = 3$

Substitute those values in to find two equations in $b$ and $c$

$\begin{array}{rcl} - 3 {(1)}^{2} + 2 b (1) + c & = & 0 \\ - 3 + 2 b + c & = & 0 \\ 2 b + c & = & 3 \end{array}$

$\begin{array}{rcl} - 3 {(3)}^{2} + 2 b (3) + c & = & 0 \\ - 27 + 6 b + c & = & 0 \\ 6 b + c & = & 27 \end{array}$

Those are simultaneous equations in $b$ and $c$
Subtract the first from the second to eliminate $c$ and find $b$
Then substitute that value into either equation to find $c$

$b = 6 c = - 9$

(b) Sketch the graph of $y = f (x)$ .

There is no constant term in $f (x)$ , so the y-intercept will be 0

Substitute the x-coordinates of the turning points into $f (x)$ to find the corresponding y-coordinates

$- {(1)}^{3} + 6 {(1)}^{2} - 9 (1) = - 1 + 6 - 9 = - 4 - {(3)}^{3} + 6 {(3)}^{2} - 9 (3) = - 27 + 54 - 27 = 0$

So the turning points are at $(1, - 4)$ and $(3, 0)$

Find the x-intercepts by solving $f (x) = 0$

$\begin{array}{rcl} - x^{3} + 6 x^{2} - 9 x & = & 0 \\ - x^{3} (x^{2} - 6 x + 9) & = & 0 \\ - x^{3} {(x - 3)}^{2} & = & 0 \end{array}$

$x = 0, x = 3$

So the x-intercepts are $(0, 0)$ and $(3, 0)$
Note that the first is also the y-intercept. and the second is also a turning point

Finally consider the shape of the curve
It's a 'negative cubic', so it's going to be 'up on the left and down on the right'
Draw a smooth curve incorporating all these features
Label the turning points and intercepts

Last updated: 20 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Graphing FunctionsNext:Graphs of Rational Functions

Graphs of Polynomials (Edexcel IGCSE Further Pure Maths)

Revision Note

Quadratic Functions & Graphs

What are the key features of quadratic graphs?

What are the equations of a quadratic function?

How do I find an equation of a quadratic?

Examiner Tips and Tricks

Worked Example

Cubic Functions & Graphs

What are the key features of cubic graphs?

How do I sketch the graph of a cubic?

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Dan Finlay

Author: Lucy Kirkham