Vector Basics (Edexcel IGCSE Further Pure Maths)

Vector Notation

What is a vector?

• Vectors represent a movement of a certain distance (magnitude) in a given direction

• In one dimension, the sign of a number represents its direction 

  • For example, two objects with velocities 7 m/s and ‑7 m/s are travelling:

    • at the same speed (magnitude)

    • but in opposite directions

• In two dimensions, vectors consist of x- and y-components
  

  • This shows movement parallel to the x  and y-axes

  • Components can be positive or negative 

What is a scalar?

• A scalar is an ordinary number that does not represent movement

  • A scalar is not a vector

• Scalars can still be negative

  • For example

    • temperature is a scalar (it's -2°C today)

    • but change in temperature is a vector (it's +3°C from yesterday)

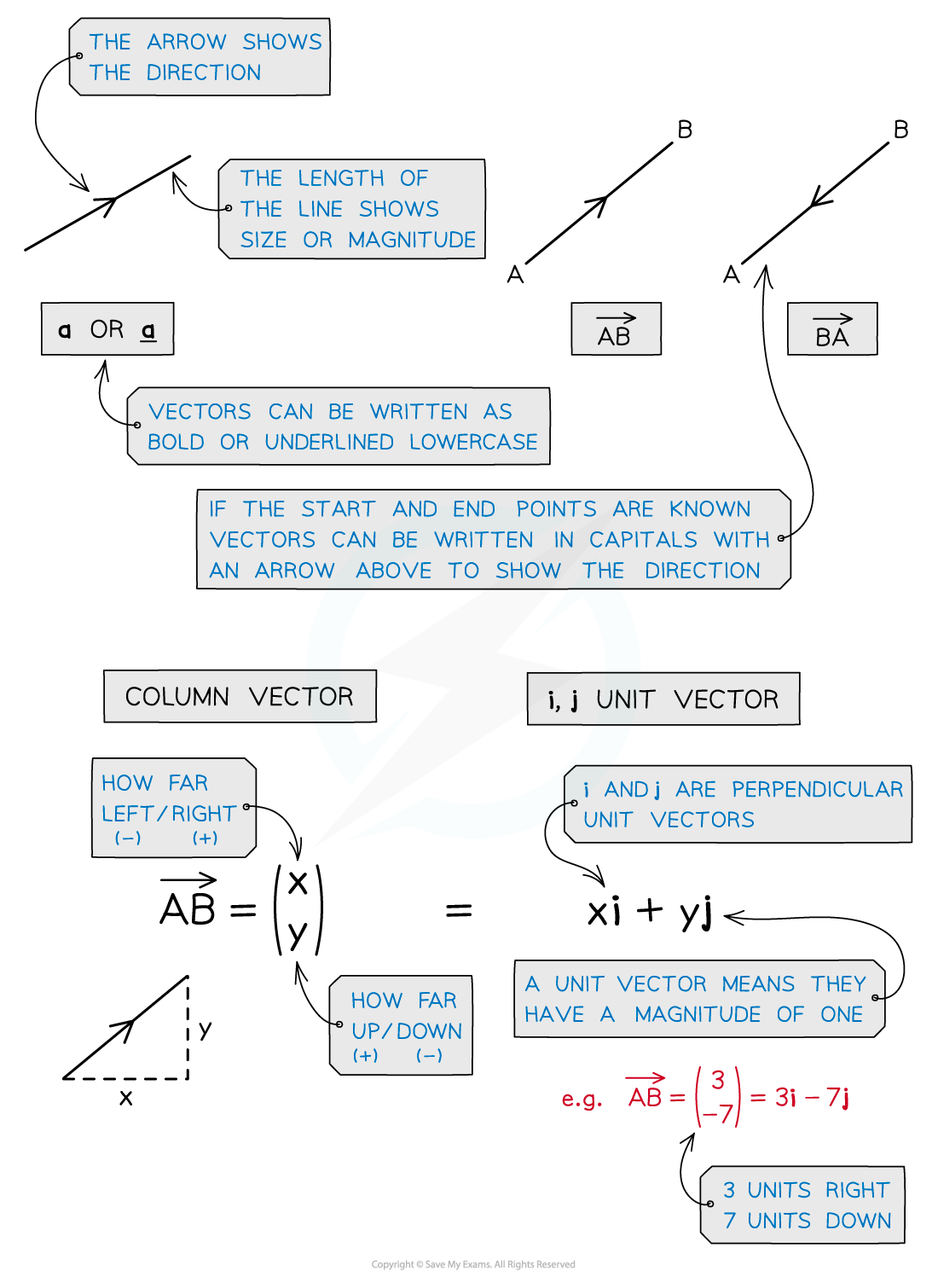
How do I write vectors?

• If you know the two components of a vector, you can write it as

  • either a column vector

    • is 3 right and 2 up

  • or in i and j notation

    • 

• If you do not know the components, use a lower-case letter to represent the entire vector

  • Exams use bold letters

    • a, b, ...

  • You should write underlined letters

    • a, b, ...

• If points (A , B , ...) are given, means the vector from A  to B

  • The order matters

Adding & Subtracting Vectors

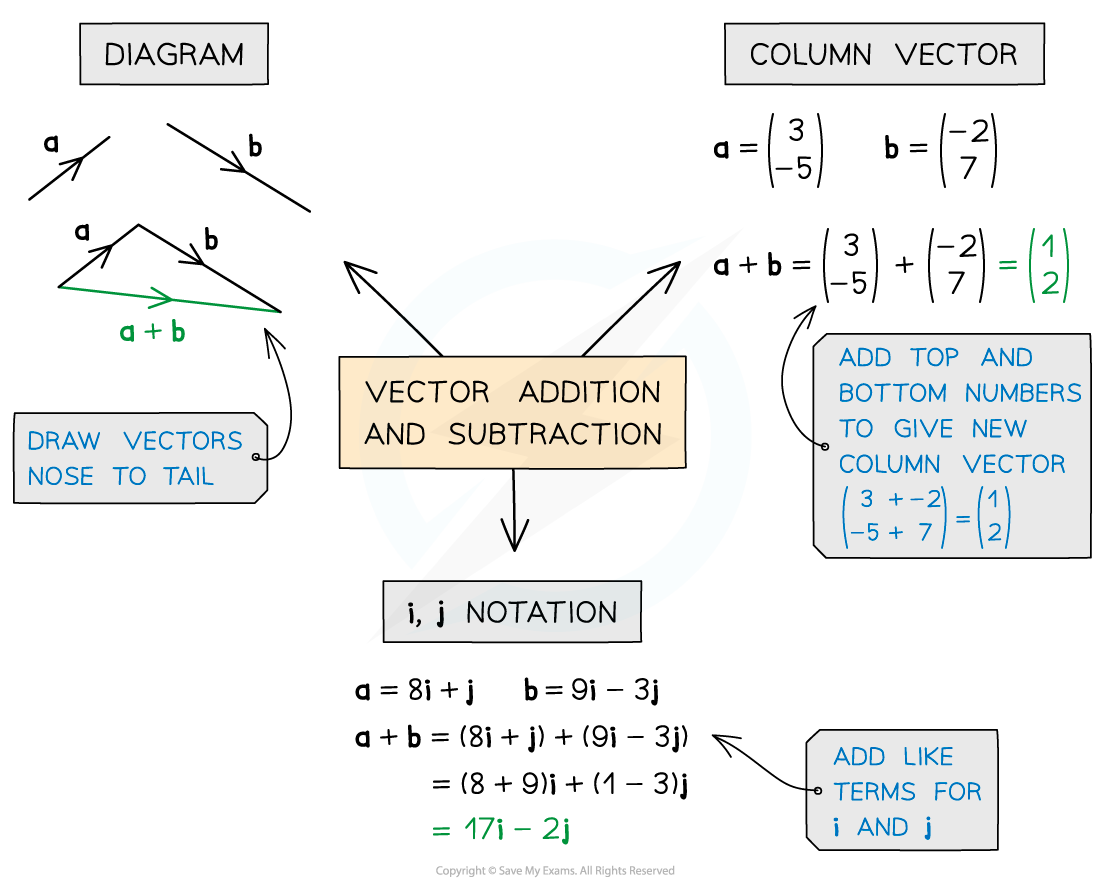
How do I add vectors?

• To add vectors you add their components

  • For column vectors, add the tops together and bottoms together

    • 

• In i and j notation, add i and j parts separately

  • (2i + j) + (i + 4j) = (3i + 5j)

• Visually, the vector a + b is the shortest route

  • from the start of a

  • to the end of b

How do I subtract vectors?

• To subtract vectors you subtract their components
  

  • 

• In i and j notation, subtract i and j parts separately

  • Be careful with brackets and negatives

    • (2i + j) - (i + 4j) = (i - 3j)

• Visually, the vector a - b is the shortest route

  • from the start of a

  • to the end of -b

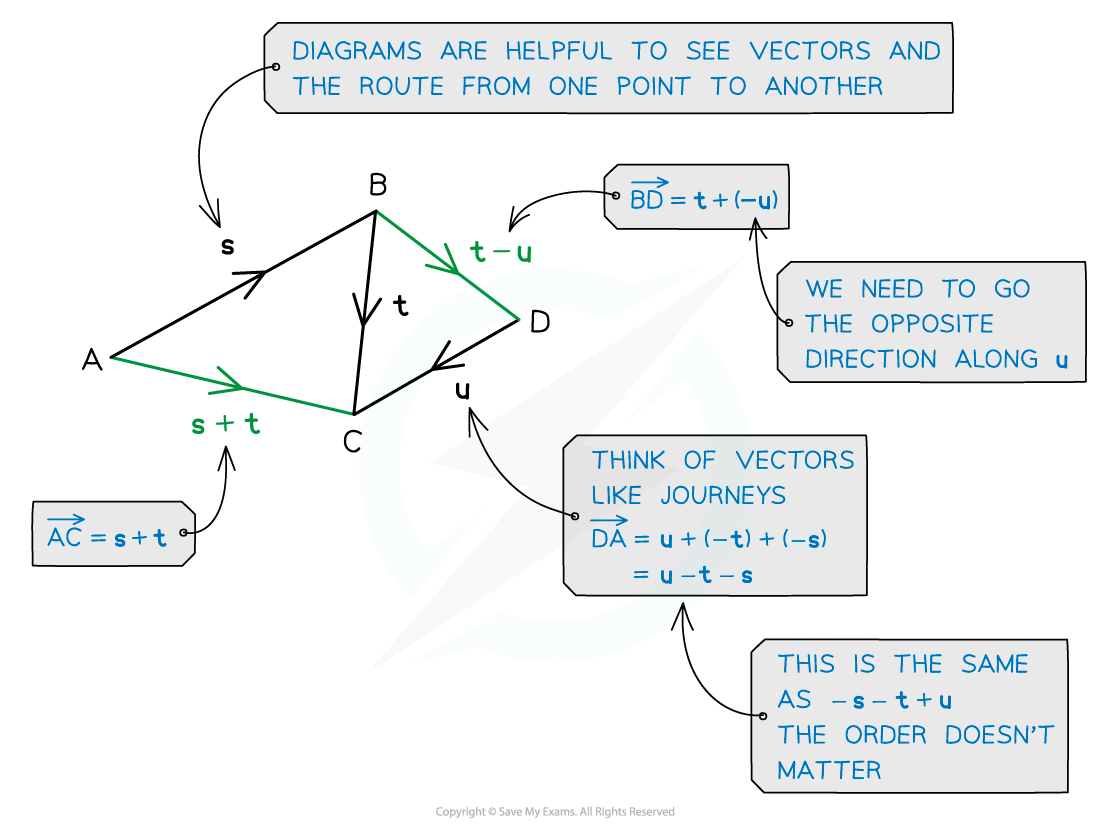
How do I add and subtract vectors on diagrams?

• Think of travelling along vectors as a journey

  • a + b means follow a, then follow b

    • This is the same as b + a

    • They both end up at the same place

• The diagram below shows vectors s, t and u

  • To get from A  to C  do s then t

    • s + t

• If you have to travel the wrong direction along a vector, add the negative of that vector

  •  To get from B  to D  do t then the reverse of u

    • t + (-u)

    • This simplifies to t - u

• A vector plus its negative gives the zero vector, 0

  • a + (-a) = 0

    • The zero is bold (or underlined)

How do I multiply a vector by a scalar?

• The vector a multiplied by a scalar (constant number) k  is ka

  • ka is parallel to a

  • k is the scale factor of enlargement

  • A negative k reverses the direction

• Multiply all components by the scalar constant

  • For example

    • 

    • 2(4i + 5j) = 8i + 10j