Position & Displacement Vectors (Edexcel IGCSE Further Pure Maths)

Revision Note

Written by: Mark Curtis

Reviewed by: Dan Finlay

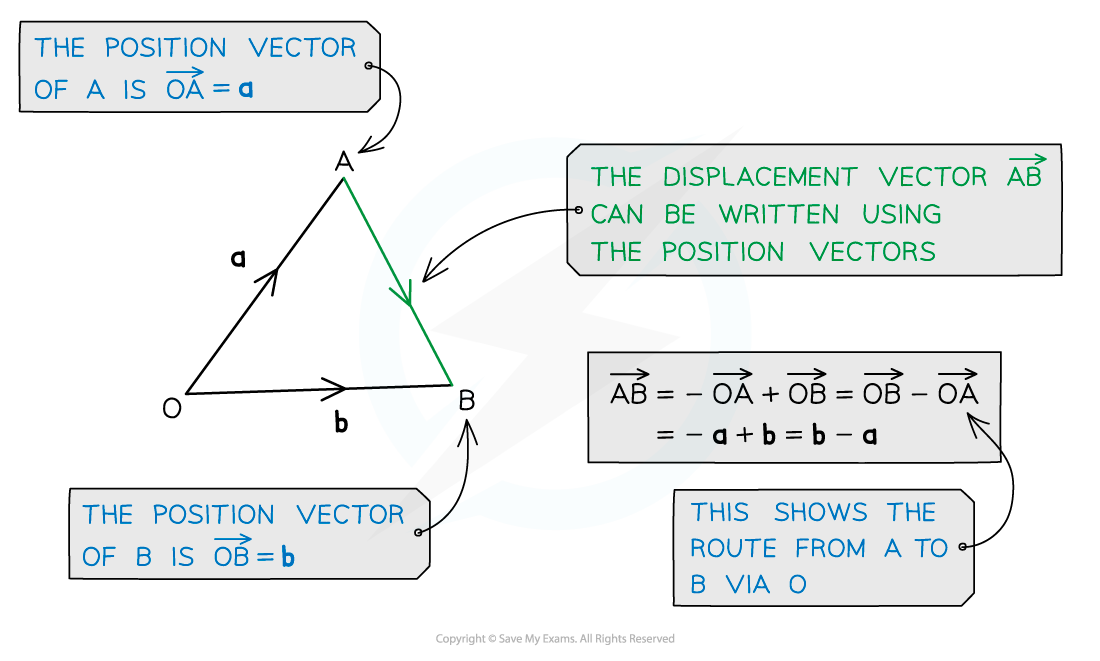
A position vector describes where a specific point, A , is, relative to a fixed origin, O
- Lower-case bold (or underlined) letters are used
  - The point A has position vector a = $\vec{O A}$
Their components are equal to their coordinates
- The point with coordinates (3, -2) has position vector 3i – 2j

A displacement vector describes the direction and distance between two points
- The displacement vector from A to B is $\vec{A B}$
  - How to get from A to B
If the points A and B have position vectors a and b relative to O
- then A to B is the same as A to O (-a) followed by O to B (b)
  - $\vec{A B} = - a + b = b - a$
  - This is a useful rule to remember

You may need to draw an origin, O , on to a diagram to be able to sketch position vectors.

The points $P$ and $Q$ have position vectors 3i + 2j and 6i - 10j respectively.

Find and simplify the vector $\vec{P Q}$ .

Let p and q be position vectors of P and Q
$\vec{P Q}$ is the displacement vector from P to Q
Use the rule that $\vec{A B} = - a + b = b - a$

$\vec{P Q} = q - p$

Substitute in p and q

$\vec{P Q} = (6 i - 10 j) - (3 i + 2 j)$

Expand and simplify

$\begin{array}{rcl} = & 6 i - 10 j - 3 i - 2 j \\ = & 3 i - 12 j \end{array}$

$\vec{P Q} = 3 i - 12 j$

Last updated: 20 October 2024

the (exam) results speak for themselves:

Did this page help you?