Polar Coordinates (Edexcel A Level Further Maths): Revision Note
Exam code: 9FM0
Intro to polar coordinates
What are polar coordinates?
Polar coordinates are an alternative way (to Cartesian coordinates) to describe the position of a point in 2D (or 3D) space
In 2D, the position of a point is described using an angle, θ and a distance, r
This is akin to “aiming in the right direction”, then “travelling so far in that direction”
Polar coordinates generally make working with circles, spirals and similar shapes easier
(3D) polar coordinates are beyond the A level syllabus but they are used with objects based on spheres such as the planets in the solar system
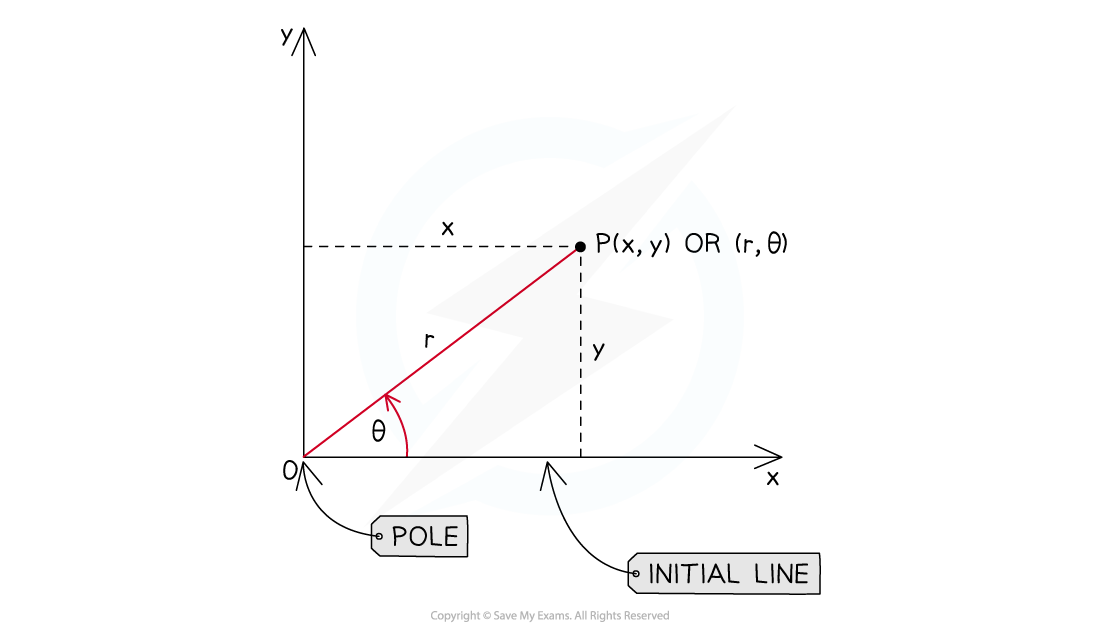
How do I describe the position of a point using polar coordinates?
Point P would be described by the coordinates (r, θ)
θ is measured in radians, anti-clockwise from the initial line (equivalent to the positive x-axis)
Negative values of θ can be used (clockwise from the initial line)
r is the (straight line) distance between the pole (origin) and point P
r is usually given as a function of θ, r = f(θ)
equations can be given implicitly too, e.g. r 2 = f(θ)
A half-line starts at the pole and extends outwards in the direction of θ
The equation of a haf-line will be of the form
, where
is a constant
The line represents positive values of r
Negative values of r are possible but are not included in Edexcel A level Further Mathematics
What is the connection between polar coordinates and Cartesian coordinates?
These results are not provided in the formulae booklet
they are easily derived from a sketch and basic trigonometry
Be careful solving
so that θ locates point P in the correct quadrant
Always use a sketch to ensure θ is measured from the initial line
Check the domain of θ to see if negative values are used
e.g. 0 ≤ θ < 2π as opposed to -π ≤ θ < π
This is very similar to the modulus-argument form of a complex number
where
and
How do I convert from polar coordinates to Cartesian coordinates?
To convert the point P(r, θ) to P(x, y)
Find the x-coordinate using
Find the y-coordinate using
In both cases take care with which quadrant P lies in
A sketch is the easiest way to double check
How do I convert from Cartesian coordinates to Polar coordinates?
To convert the point P(x, y) to P(r, θ)
Find r using Pythagoras’ theorem
r will (generally) take the positive square root since it is a distance (from the pole)
(It is possible for r to be negative, depending on the nature of f(θ))
Find θ by using a sketch in association with
Use the sketch to ensure θ locates point P in the correct quadrant
There may be the need to add or subtract π to get θ in the correct quadrant
Examiner Tips and Tricks
Ensure your calculator is in radians mode when working with polar coordinates
Note how polar coordinates (r, θ) are given in the order r then θ, even though
Worked Example
(a) Convert the polar coordinates to Cartesian coordinates.

(b) Convert the Cartesian coordinates to polar coordinates.

Sketching curves in polar form
How do I sketch curves given in polar coordinates/polar form?
Recognising common graphs and the style of their equations is important
There are three basic equations to be familiar with
is the equation of a half-line from the pole in the direction
radians anti-clockwise from the initial line
is a circle, centre at the pole with radius
is a spiral, starting at the pole where
is a positive constant
Other common types of polar curve encountered are summarised in the diagram below
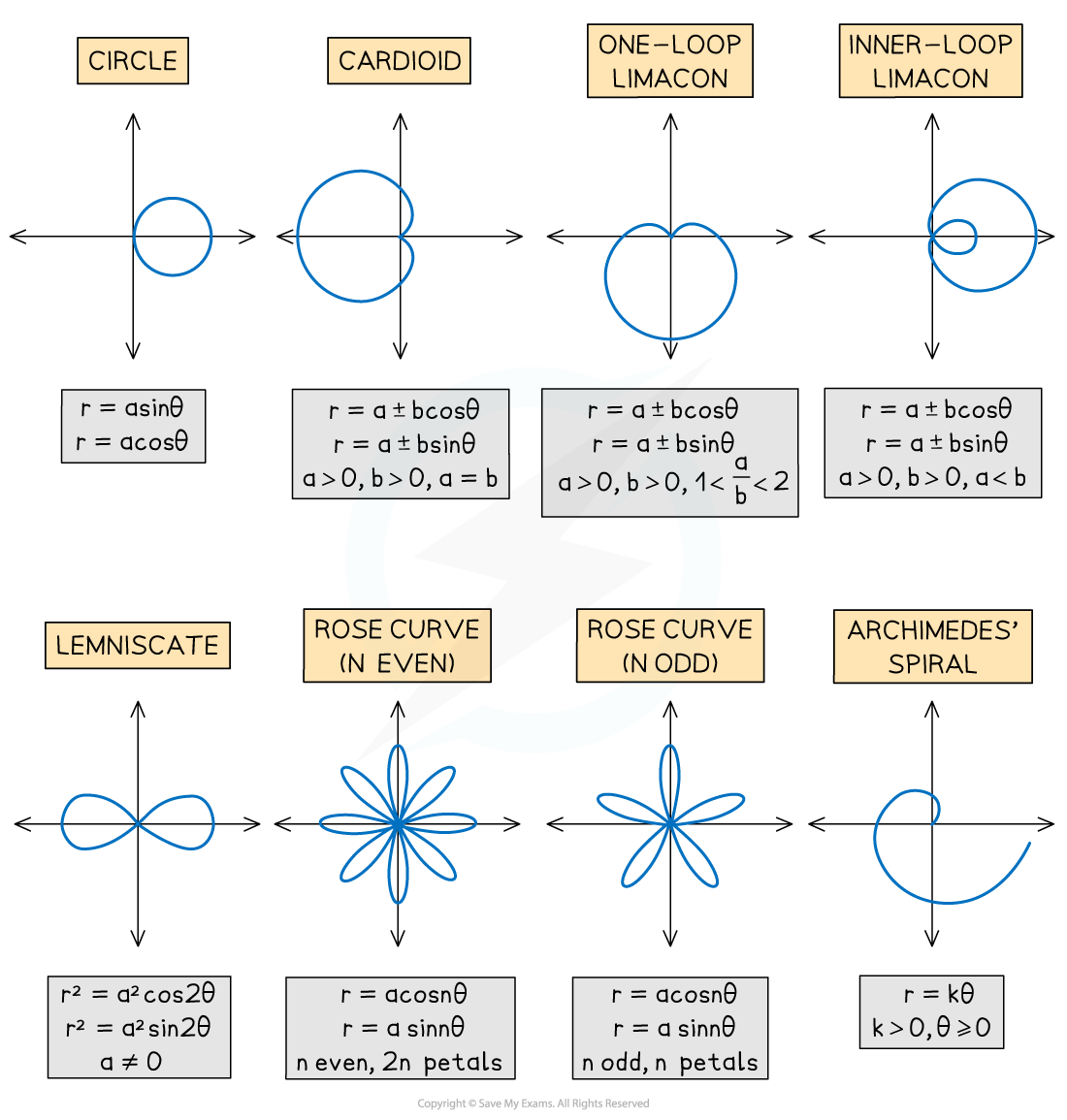
The cardioid and one-loop limacon have a cusp at the pole
For Rose Curves when n is even, half of the petals are where r > 0 and half of them are where r < 0
For Rose Curves when n is odd, the petals are drawn twice – once when r > 0 and once when r < 0
(The positive and negative petals sit on top of each other)
Some graphing software will plot negative values of r with a dotted curve
How are horizontal and vertical lines described in polar coordinates?
Straight lines have polar equations of the form
For the horizontal line corresponding to
,
where k is odd
For the vertical line corresponding to
,
where k is an integer
Diagonal lines are formed using other values of
How do I plot curves given in polar coordinates/polar form?
For more unusual polar equations a table of r and θ values can be generated
Using the table points, can be plotted and joined on polar graph paper
Values of θ may be given, e.g. every
radians

Where they are not given, think about common multiples of π that suit the question
e.g. if 3θ is involved in the question,
or
may be suitable
Use a calculator to find the corresponding values of r
Be accurate but using decimals here is fine
It is usual for questions to only require the plotting of part of a polar curve e.g. plotting within a domain of θ that completes a ‘loop’ e.g. a restricted domain of θ that produces only positive values of r
When practising problems and revising have some graphing software running so you can quickly check your sketches against an accurate diagram
Worked Example
On separate diagrams, sketch the graph of the following polar curves
(i) for
(ii)
(iii) for



Polar curve to Cartesian equation
How do I convert a polar equation to a Cartesian equation?
For equations of the form r = f(θ) square both sides
Some questions may define r2 rather than r
r2 can then be replaced by x2 + y2
To eliminate θ, some manipulation and use of trigonometric identities may be needed
Aim to convert terms involving θ into either the form
or
then convert to x and y
e.g. If
then
Awkward powers of r may be involved but these can be manipulated into terms of r2 too e.g.
How do I convert a Cartesian equation to a polar equation?
In general substitute
and
into the Cartesian equation and simplify/rearrange
Trigonometric identities may be involved
If you spot them, there may be some shortcuts e.g. ‘hidden’ sums of
and
such as in
Examiner Tips and Tricks
When converting a polar equation to a Cartesian equation, unless required by the question, do not worry about rearranging into the form
Make any obvious simplifications but otherwise an implicit Cartesian form is fine
Worked Example
(a) Find a Cartesian equation of the polar curve .
(b) Find a polar equation in the form for the ellipse
.

Intersections of polar curves
How do I find the intersections of two curves given in polar form?
This is essentially the same as solving simultaneous equations
The aim is to eliminate one of the variables (usually r) and solve for the other
Any previous skills used to eliminate variables may still be useful here
The general approach is to write the two equations in the forms
and
Then solve
If required, substitute θ into f(θ) or g(θ) to find r
Be aware that polar curves are often given in the form
Working with r2 rather than r may be easier
Skills beyond basic simultaneous equations include
using trigonometric identities and solving trigonometric equations
“squaring and adding” (this is a common technique)
this can produce very useful
and/or
terms!
Examiner Tips and Tricks
Calculators are unlikely to be able to solve these types of simultaneous equations directly
They may have a ‘solve’ mode you can use once the equation has been reduced to a single variable
However look out for when questions require exact answers
Worked Example
The diagram below shows a sketch of the polar graphs of and
for
.

a) Find the smallest positive values of for which each curve crosses the pole.
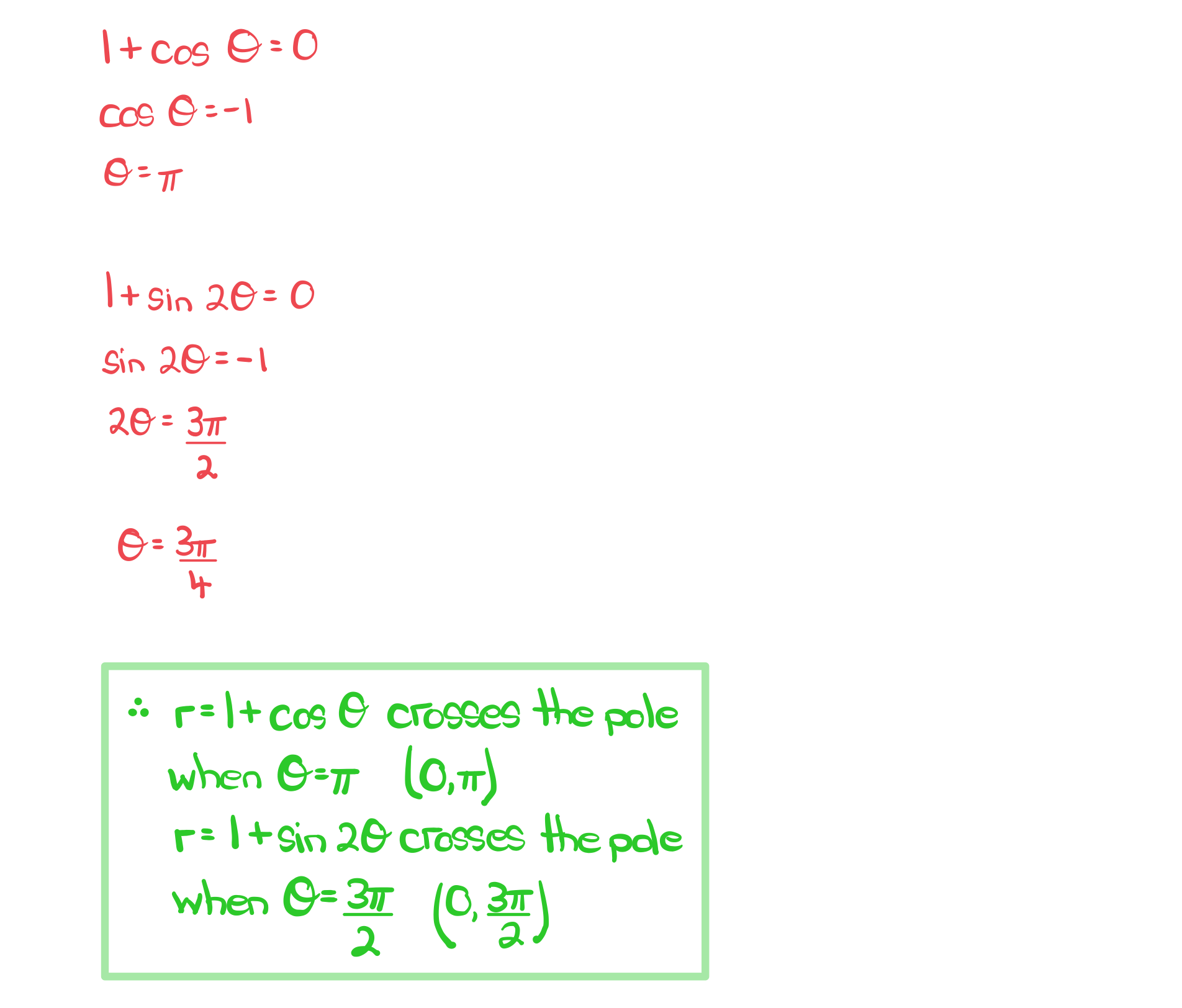
b) For , find the points of intersection between the two curves for
.


Unlock more, it's free!
Did this page help you?