Angular Velocity (OCR A Level Physics)

Angular Displacement

• In circular motion, it is more convenient to measure angular displacement in units of radians rather than units of degrees
• Angular displacement is defined as:

The change in angle, in radians, of a body as it rotates around a circle

• This can be summarised in equation form:

• Where:
  • Δθ = angular displacement, or angle of rotation (radians)
  • S = length of the arc, or the distance travelled around the circle (m)
  • r = radius of the circle (m)

• Note: both distances must be measured in the same units e.g. metres

Angular Speed

• Any object travelling in a uniform circular motion at the same speed travels with a constantly changing velocity
  • This is because it is constantly changing direction, and is therefore accelerating
• The angular speed (⍵) of a body in circular motion is defined as:

The rate of change in angular displacement with respect to time

• Angular speed is a scalar quantity and is measured in rad s^-1
• It can be calculated using:

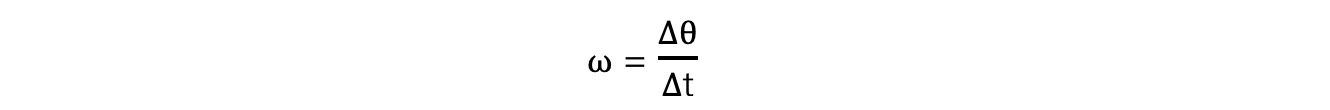
• Where:
  • Δθ = change in angular displacement (radians)
  • Δt = time interval (s)

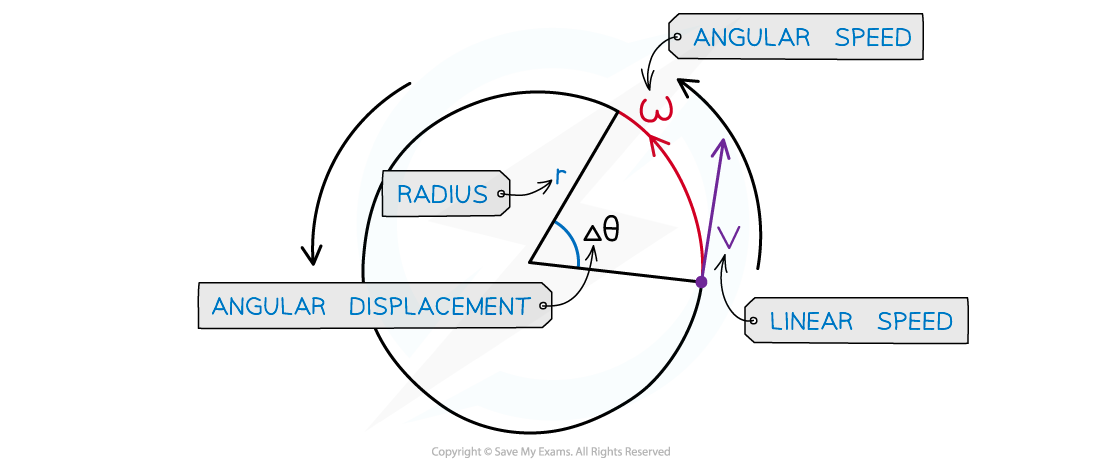
When an object is in uniform circular motion, velocity constantly changes direction, but the speed stays the same

• Taking the angular displacement of a complete cycle as 2π, the angular speed ⍵ can be calculated using the equation:

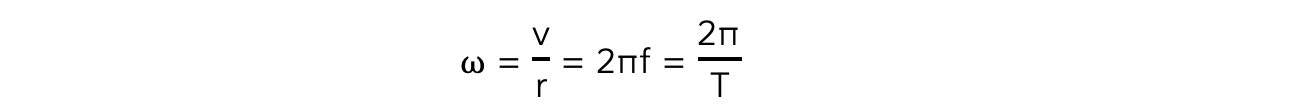
• Where:
  • v = linear speed (m s^-1)
  • r = radius of orbit (m)
  • T = the time period (s)
  • f = frequency (Hz)

• Angular velocity is the same as angular speed, but it is a vector quantity
• This equation shows that:
  • The greater the rotation angle θ in a given amount of time, the greater the angular velocity ⍵
  • An object rotating further from the centre of the circle (larger r) moves with a smaller angular velocity (smaller ⍵)