Velocity (OCR A Level Physics) : Revision Note

Velocity of an Oscillator

• The velocity of an object in simple harmonic motion varies as it oscillates back and forth

  • Since velocity is a vector, the velocity of the oscillator is its speed in a certain direction

• The maximum velocity of an oscillator is at the equilibrium position i.e. when its displacement is zero

• The velocity of an oscillator in SHM is defined by:

• Where:

  • = velocity (m s^-1)

  • = maximum velocity (m s^-1)

  • = angular frequency (rad s^-1)

  • = time (s)

• This is a cosine function if the object starts oscillating from the equilibrium position ( when )

• The velocity of an oscillator is related to its displacement by:

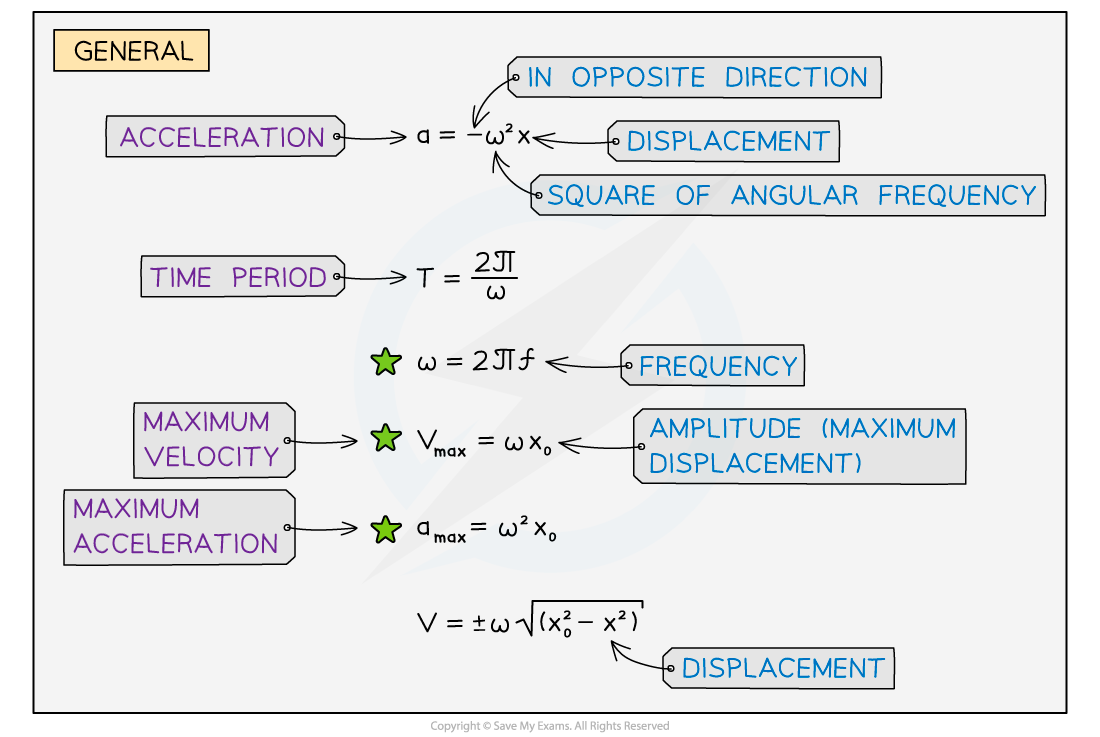
• Where:

  • = displacement (m)

  • = amplitude (m)

  • ± = ‘plus or minus’. The value can be negative or positive

• This equation shows that

  • The greater the amplitude of an oscillation, the greater its velocity when passing through the equilibrium position (at )

• The maximum velocity of an oscillator is therefore given by:

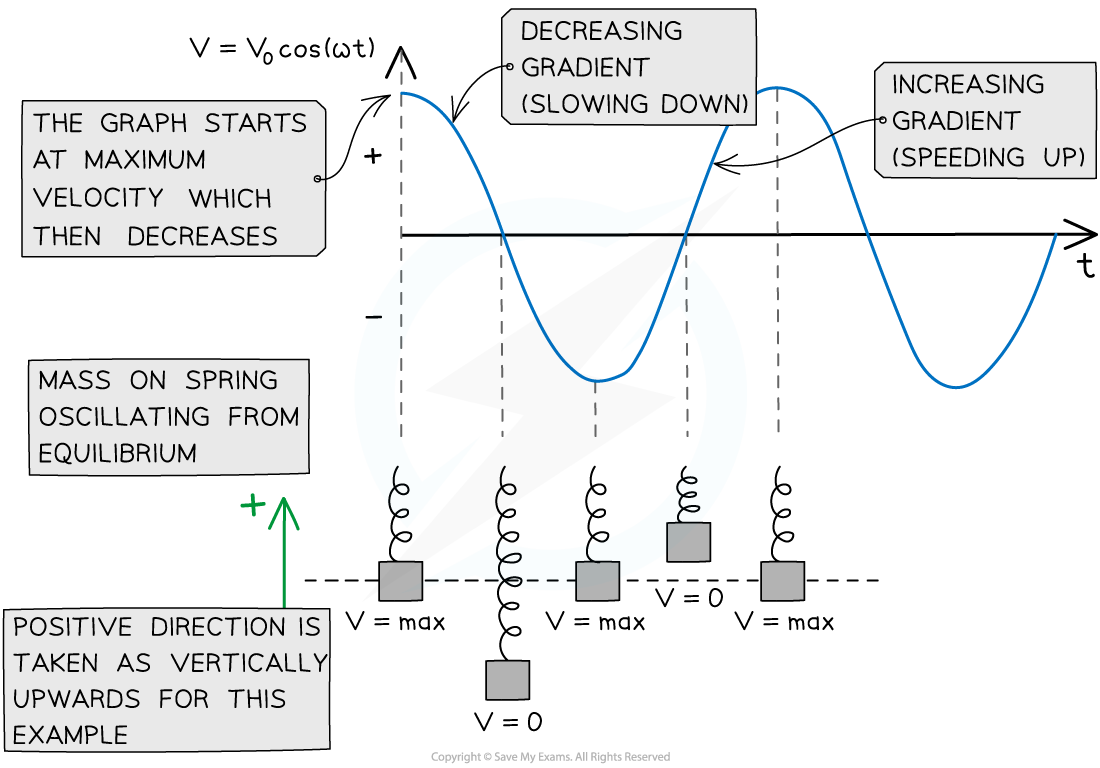
The variation of the speed of a mass on a spring in SHM over one complete cycle