Nodes & Antinodes (OCR A Level Physics): Revision Note
Exam code: H556
Nodes & Antinodes
A stationary wave is made up nodes and antinodes
Nodes are regions where there is no vibration
Antinodes are regions where the vibrations are at their maximum amplitude
The nodes and antinodes do not move along the string
Nodes are fixed and antinodes only move in the vertical direction
The phase difference between two points on a stationary wave are either in phase or out of phase
Points between nodes are in phase with each other
Points that have an odd number of nodes between them are out of phase
Points that have an even number of nodes between them are in phase
The image below shows the nodes and antinodes on a snapshot of a stationary wave at a point in time
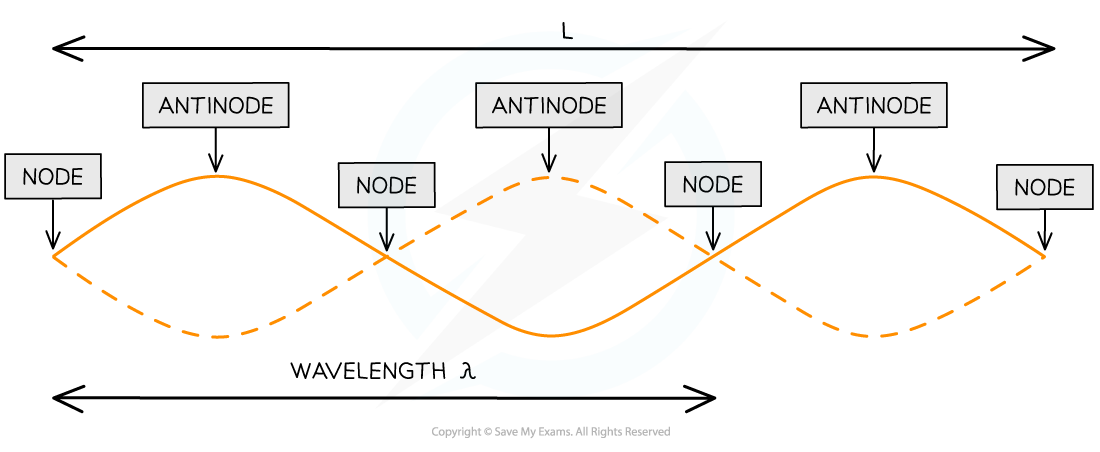
One wavelength on a stationary wave is only a proportion of its full length
Where:
L is the length of the string
One wavelength λ is only a portion of the length of the string
Worked Example
A stretched string is used to demonstrate a stationary wave, as shown in the diagram.

Which row in the table correctly describes the length of L and the name of X and Y?
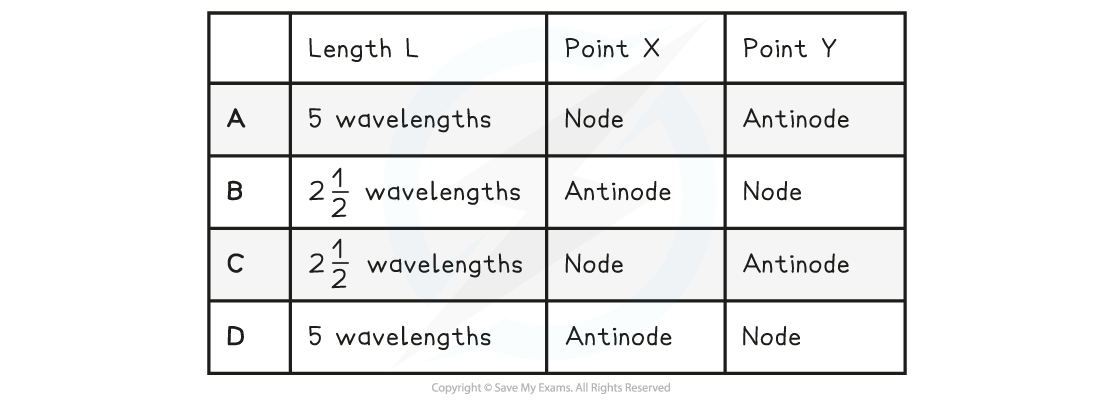
Answer: C

Examiner Tips and Tricks
Make sure you learn the definitions of node and antinode:
Node = A point of minimum or no disturbance
Antinode = A point of maximum amplitude
In exam questions, the lengths of the strings will only be in whole or half wavelengths. For example, a wavelength could be made up of 3 nodes and 2 antinodes or 2 nodes and 3 antinodes.
Calculating Wavelength from Nodes & Antinodes
The wavelength λ of a stationary wave can be determined by the separation between adjacent nodes (or antinodes)
The separation between adjacent nodes or antinodes is equal to λ / 2
Adjacent means two nodes or antinodes that are next to each other
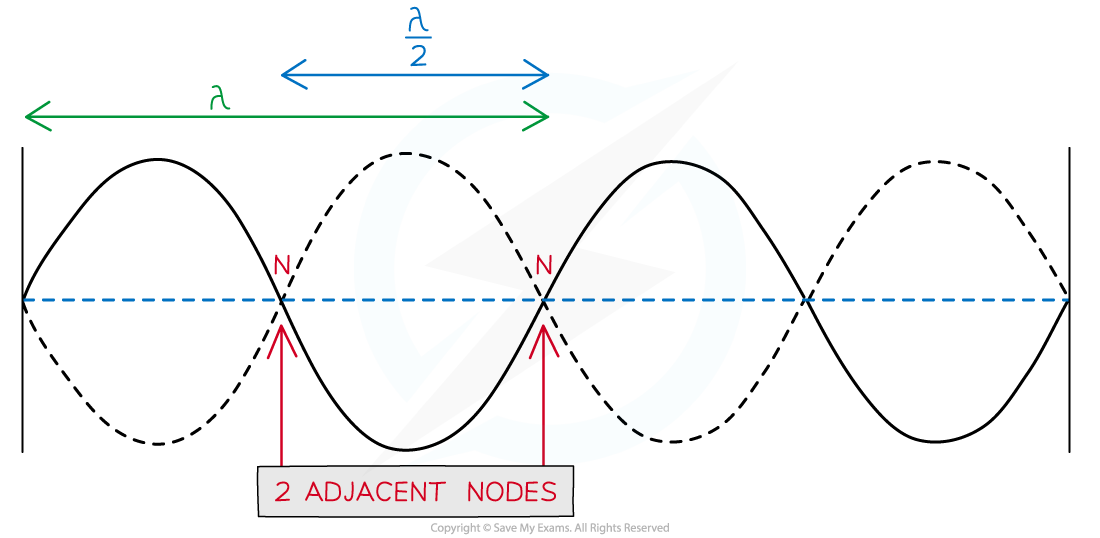
2 adjacent nodes are nodes that are directly next to each other
Worked Example
The stationary wave below has a length L of 15 cm.

Calculate the wavelength λ of the wave.
Answer:
Step 1: Calculate the distance between two nodes
Distance between two nodes = 15 cm ÷ 3 = 5 cm
Step 2: Calculate λ
Distance between two nodes = λ / 2 = 5 cm
λ = 2 × 5cm = 10 cm

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?