IBPhysicsDPHLRevision NotesThe Particulate Nature of MatterGreenhouse EffectEnergy Balance Problems

Energy Balance Problems (DP IB Physics) : Revision Note

Katie M

Author

Katie M

Last updated

Energy Balance Problems

  • It is useful to consider Earth’s energy balance in terms of how much incoming energy from the Sun is used and how much is returned to space

  • If incoming and outgoing energy are in balance, the Earth’s temperature will remain constant

  • This can be used to create models which can help climate scientists predict temperature fluctuations based on current and increased concentrations of greenhouse gases

    • At it’s simplest, the model involves a one-layer atmosphere above the Earth’s surface

Worked Example

The diagram below shows a simple energy balance climate model in which the atmosphere and the Earth’s surface are treated as two bodies.

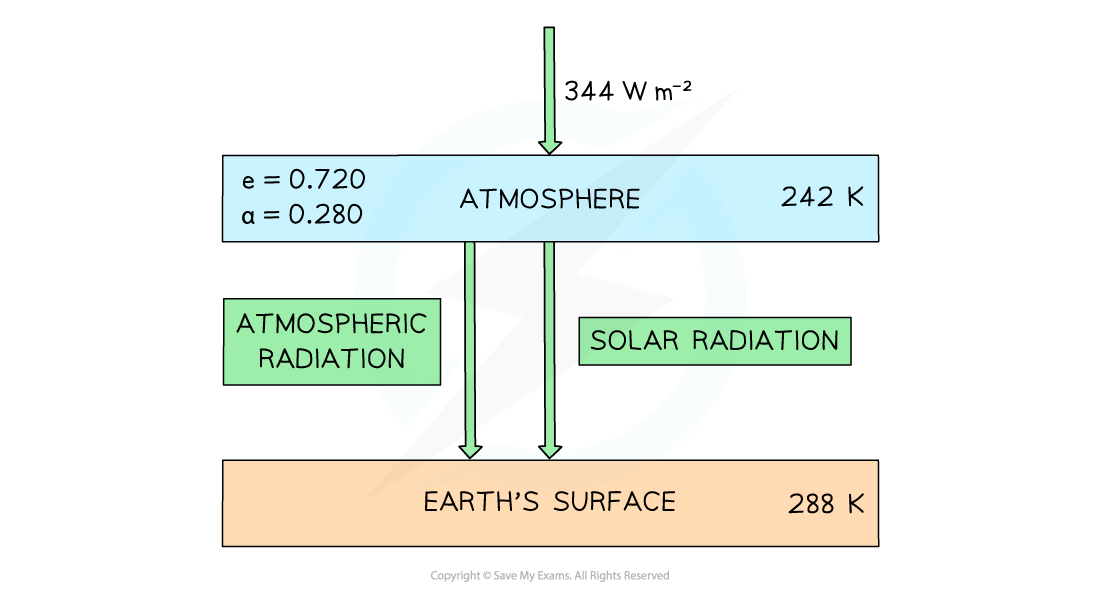
8-2-5-we-energy-system_sl-physics-rn

The Earth’s surface receives both solar radiation and radiation emitted from the atmosphere.

At current atmospheric greenhouse gas concentrations, the temperature of Earth’s atmosphere is set to increase by 6 K.

Data for this model:

  • Current mean temperature of the Earth’s atmosphere = 242 K

  • Current mean temperature of the Earth’s surface = 288 K

  • Solar intensity per unit area at top of the atmosphere = 344 W m–2

  • Emissivity of the atmosphere, e = 0.720

  • Albedo of the atmosphere, a = 0.280

Use this data to estimate the increase in temperature of the Earth’s surface.

Answer:

Step 1: List the known quantities

  • Solar intensity above atmosphere, Ia = 344 W m–2

  • Emissivity of the atmosphere, e = 0.720

  • Emissivity of the surface, e = 1

  • New temperature of Earth’s atmosphere, Ta = 242 + 6 = 248 K

  • Stefan-Boltzmann constant, σ = 5.67 × 10–8 W m–2 K–4

  • Intensity absorbed at the Earth’s surface = Is

  • New temperature of Earth’s surface = Ts

Step 2: Calculate the solar intensity absorbed at the Earth’s surface

  • This can be calculated using the emissivity and the solar intensity above the atmosphere

Is = e × Ia

Is = 0.720 × 344 = 247.68 = 248 W m–2

Step 3: Write the equation for the power per unit area emitted by a body

  • Since intensity = power per unit area

I = eσT4

Step 4: Calculate the new intensity radiated by the atmosphere

I = 0.720 × (5.67 × 10–8) × 2484 = 154.43 = 154 W m–2

Step 5: Calculate the new intensity absorbed by the Earth’s surface

  • The intensity absorbed by the Earth’s surface is a sum of the solar radiation that reaches the surface plus the intensity radiated by the atmosphere

New intensity, Is = 248 + 154 = 402 W m–2

Step 6: Calculate the new temperature of the Earth’s surface

  • The Earth’s surface can be assumed to be a black body, hence e = 1

Is = σTs4

400 = (5.67 × 10–8) × Ts4

Ts = fourth root of fraction numerator 400 over denominator 5.67 cross times 10 to the power of negative 8 end exponent end fraction end root = 290 K

Step 7: Determine the increase in temperature

ΔT = 290 – 288 = 2 K

Examiner Tips and Tricks

In simplified climate models, you can generally assume the Earth’s surface and the atmosphere:

  • Act as black bodies - this means the emissivity of the surface will be equal to 1!

  • Remain at a constant temperature

👀 You've read 0 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourselfFlashcards

Did this page help you?

Previous:The Greenhouse EffectNext:Gas Pressure
Katie M

Author: Katie M

Expertise: Physics Content Creator

Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

Download notes on Energy Balance Problems