Direct Proportion (Cambridge (CIE) IGCSE Maths) : Revision Note

Direct Proportion

What is direct proportion?

• Proportion is a way of talking about how two variables are related to each other

• Direct proportion means that as one variable goes up the other goes up by the same factor

  • The ratio between the two amounts will always stay the same

• The symbol means "proportional to"

  • E.g. y is directly proportional to x, yx

• If x and y are directly proportional, then

  • x : y will always be the same

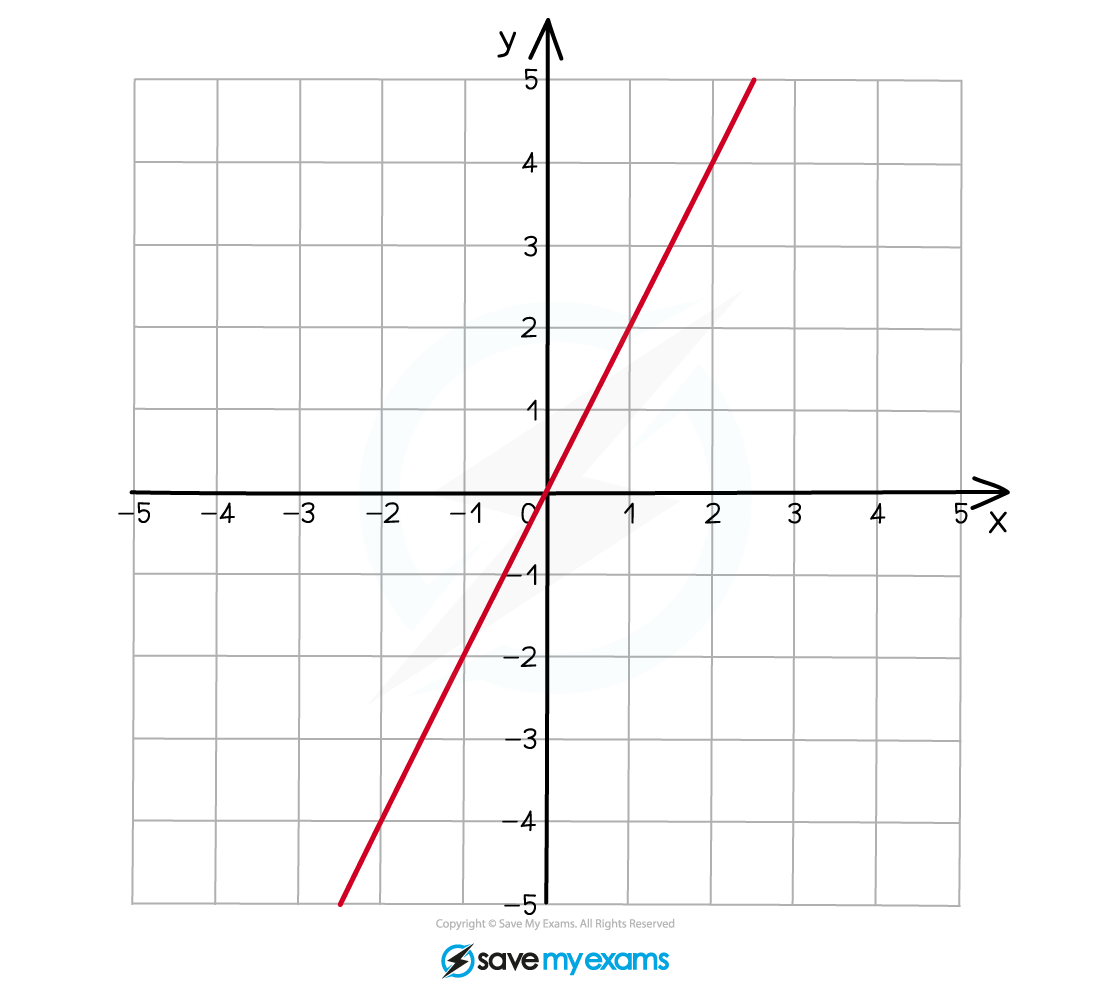
  • there will be some value, k, such that y = kx

  • the graph relating x and y is a linear graph, with gradient k

• k is called the constant of proportionality

How do I use direct proportion with powers and roots?

• Problems may involve a variable being directly proportional to a power or root of another variable

• For example

  • y is directly proportional to the square of x

    • 

    • means that

  • y is directly proportional to the square root of x

    • 

    • means that

  • y is directly proportional to the cube of x

    • 

    • means that

  • y is directly proportional to the cube root of x

    • 

    • means that

  • Each of these would have a different type of graph, depending on the power or root

How do I find the equation between two directly proportional variables?

• Direct proportion questions always have the same process:

  • STEP 1
    Identify the two variables and write down the formula in terms of k

    • E.g. y is directly proportional to x

    • write down the formula

  • STEP 2
    Find k by substituting any given values from the question into your formula, then solving to get k

    • E.g. if you are told y = 6 when x = 2

    • then giving

  • STEP 3
    Rewrite the formula with the known value of k from above (substitute it in)

    • 

    • This is the equation relating the two variables

  • STEP 4
    Use the equation to answer other parts of the question

    • E.g. find y when x = 10

    • gives