Centripetal Acceleration (OCR A Level Physics): Revision Note

Centripetal Acceleration

• Centripetal acceleration is defined as:

  The acceleration of an object towards the centre of a circle when an object is in motion (rotating) around a circle at a constant speed

• It can be defined using the radius r and linear speed v:

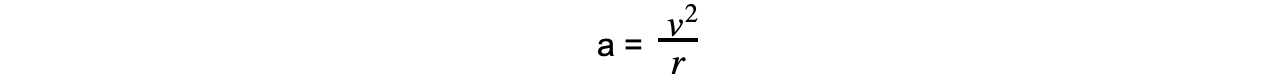
• Using the equation relating angular speed ω and linear speed v:

 v = r⍵

• These equations can be combined to give another form of the centripetal acceleration equation:

• This equation shows that centripetal acceleration is equal to the radius times the square of the angular speed

• Alternatively, rearrange for r:

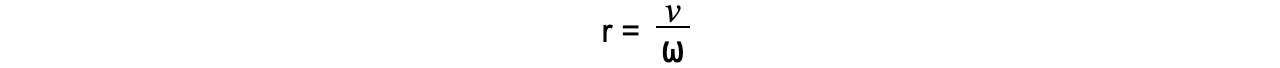
• This equation can be combined with the first one to give us another form of the centripetal acceleration equation:

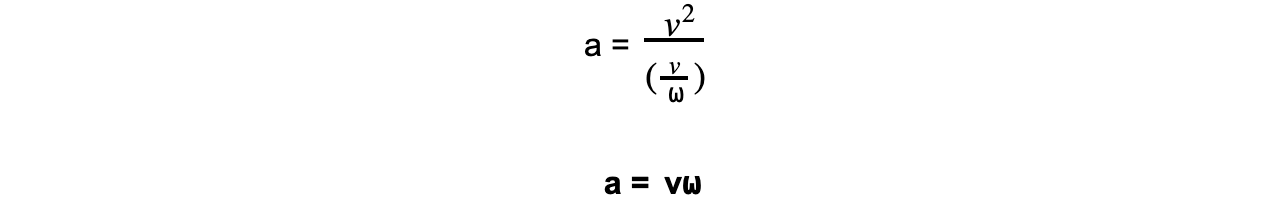
• This equation shows how the centripetal acceleration relates to the linear speed and the angular speed

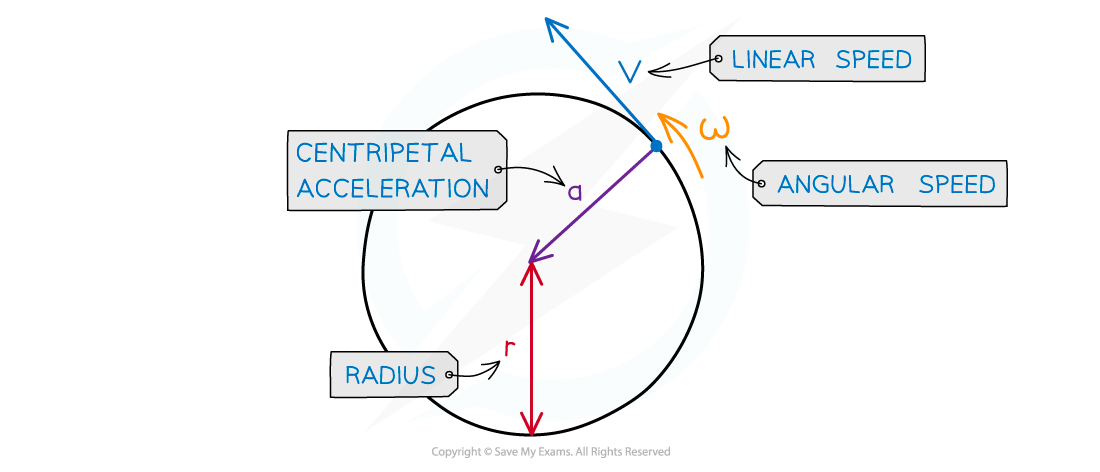
Centripetal acceleration is always directed toward the centre of the circle, and is perpendicular to the object’s velocity

• Where:

  • a = centripetal acceleration (m s⁻²)

  • v = linear speed (m s⁻¹)

  • ⍵ = angular speed (rad s⁻¹)

  • r = radius of the orbit (m)