Time Period & Frequency (OCR A Level Physics): Revision Note
Exam code: H556
Period & Amplitude of a Simple Harmonic Oscillator
An oscillator in simple harmonic motion is an isochronous oscillation, which means:
The period of oscillation is independent of the amplitude
Therefore, an object is said to perform simple harmonic oscillations when all of the following apply:
The oscillations are isochronous
There is a central equilibrium point
The object's displacement, velocity and acceleration change continuously
There is a restoring force always directed towards the equilibrium point
The magnitude of the restoring force is proportional to the displacement

Determining the Period & Frequency of Simple Harmonic Oscillations
Equipment List

Resolution of measuring equipment:
Stopwatch = 0.01 s
Metre Ruler = 1 mm
SHM in a Mass-Spring System
The overall aim of this experiment is to calculate the spring constant of a mass-spring system
This is done by investigating how the time period of the oscillations varies with the mass
This is just one example of how this required practical might be carried out
Variables
Independent variable = mass, m
Dependent variable = time period, T
Control variables:
Spring constant, k
Number of oscillations
Method

The setup of apparatus to detect oscillations of a mass-spring system
Set up the apparatus, with no masses hanging on the holder to begin with (just the 100 g mass attached to it)
Pull the mass hanger vertically downwards between 2-5 cm as measured from the ruler and let go. The mass hanger will begin to oscillate
Start the stopwatch when it passes the nail marker
Stop the stopwatch after 10 complete oscillations and record this time. Divide the time by 10 for the time period (which is the mean)
Add a 50 g mass to the holder and repeat the above between 8-10 readings. Make sure the mass is pulled down by the same length before letting go
An example table might look like this:

Analysing the Results
The time period of a mass-spring system is given by:
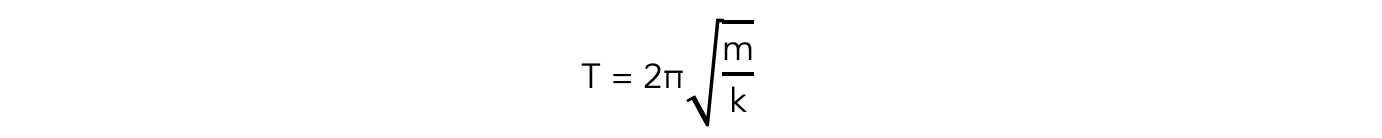
Where:
T = time period (s)
m = mass (kg)
k = spring constant (N m–1)
Squaring both sides of the equation gives:

Comparing this to the equation of a straight line: y = mx
y = T2
x = m
Gradient = 4π2 / k
Plot a graph of T2 against m and draw a line of best fit
Calculate the gradient
The spring constant, k, is therefore equal to:

The spring constant can also be found using the Hooke’s Law equation (F = -kx)
An experiment can be carried out and k found from the gradient of a plot of the force F against the extension x
The two values could then be compared

SHM in a Simple Pendulum
The overall aim of this experiment is to calculate the acceleration due to gravity from a simple pendulum
This is done by investigating how the time period of its oscillations varies with its length
This is just one example of how this required practical might be carried out
Variables
Independent variable = length, L
Dependent variable = time period, T
Control variables:
Mass of pendulum bob, m
Number of oscillations
Method

Set up the apparatus, with the length of the pendulum at 0.2 m
Make sure the pendulum hangs vertically downwards at equilibrium and inline directly in front of the needle marker
Pull the pendulum to the side at a very small angle then let go. The pendulum will begin to oscillate
Start the stopwatch when the pendulum passes the needle marker. One complete oscillation is when the pendulum passes through the equilibrium, then to one amplitude and the other and then back to the equilibrium again (not just from side to side)
Stop the stopwatch after 10 complete oscillations and record this time. Divide the time by 10 for the time period (which is the mean)
Increase the length of the pendulum by adjusting the string and the wooden block and repeat the above for 8-10 readings. The ruler is used to measure the string and ensure it is measured from the wooden blocks to the centre of mass of the bob. Also, make sure the mass is pulled to the side by the same angle before letting go for the oscillations

An example table might look like this:

Analysing the Results
The time period of a simple pendulum is given by:
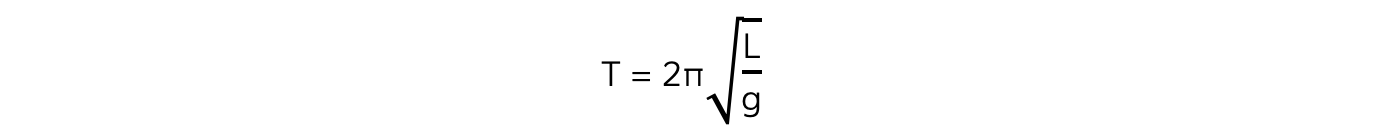
Where:
T = time period (s)
L = length of the pendulum (m)
g = acceleration due to gravity (m s–2)
Squaring both sides of the equation gives

Comparing this to the equation of a straight line: y = mx + c
y = T2
x = L
gradient m = 4π2 / g
c = 0
Plot a graph of T2 against L and draw a line of best fit
Calculate the gradient
The acceleration due to gravity is equal to:


Evaluating the Experiments
Systematic Errors:
Reduce parallax error by being at eye level with the marker
Random Errors:
Record the time taken for 10 full oscillations, then divide by 10 for one period, to reduce random errors
The oscillations may not completely go from side to side, and end up in a circle. Therefore, keep the amplitudes relatively small (only a few cm) and repeat the readings if they do take a different trajectory
A motion tracker and data logger could provide a more accurate value for the time period and reduce the random errors in starting and stopping the stopwatch (due to reflex times)
The equation for the time period of a pendulum bob only works for small angles, so make sure the pendulum is not pulled too far out to the side for the oscillations
For the mass-spring system, the oscillations may not stay completely vertical. Therefore, keep the amplitudes relatively small (only a few cm) and repeat the reading making sure they are vertical
Safety Considerations
The suspended masses or pendulum bob could damage the surface if they were to fall. Make sure to keep a soft surface directly below the equipment
Only pull down the mass and spring system a few centimetres for the oscillations, as larger oscillations could cause the masses to fall off and damage the equipment
The wooden blocks must be tightly clamped together to hold the string for the pendulum in place, otherwise the pendulum may dislodge during oscillations and fall off
Worked Example
A student investigates the relationship between the time period and the mass on a mass-spring system that oscillates with simple harmonic motion. They obtain the following results.

Calculate the value of the spring constant of the spring used in this experiment
Answer:
Step 1: Complete the table
Add the extra column T2 and calculate the values

Step 2: Plot the graph of T2 against the mass m

Make sure the axes are properly labelled and the line of best fit is drawn with a ruler
Step 3: Calculate the gradient of the graph

The gradient is calculated by:

Step 4: Calculate the spring constant, k


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?