Energy in SHM (OCR A Level Physics): Revision Note
Exam code: H556
Kinetic & Potential Energies
During simple harmonic motion, energy is constantly exchanged between two forms:
Kinetic energy
Potential energy
The potential energy could be in the form of:
Gravitational potential energy (for a pendulum)
Elastic potential energy (for a horizontal mass on a spring)
Or both (for a vertical mass on a spring)
The speed of an oscillator is at a maximum when displacement x = 0, so:
The kinetic energy of an oscillator is at a maximum when the displacement is zero
This is because kinetic energy is equal to
so when the oscillator moves at maximum velocity (at the equilibrium position) it reaches its maximum value of kinetic energy
Therefore, the kinetic energy is zero at maximum displacement x = x0, so:
The potential energy of an oscillator is at a maximum when the displacement (both positive and negative) is at a maximum,
This is because the kinetic energy is transferred to potential energy as the height above the equilibrium position increases, since potential energy is equal to mgh
A simple harmonic system is therefore constantly converting between kinetic and potential energy
When one increases, the other decreases and vice versa, therefore:
The total energy of a simple harmonic system always remains constant
The total energy is, therefore, equal to the sum of the kinetic and potential energies
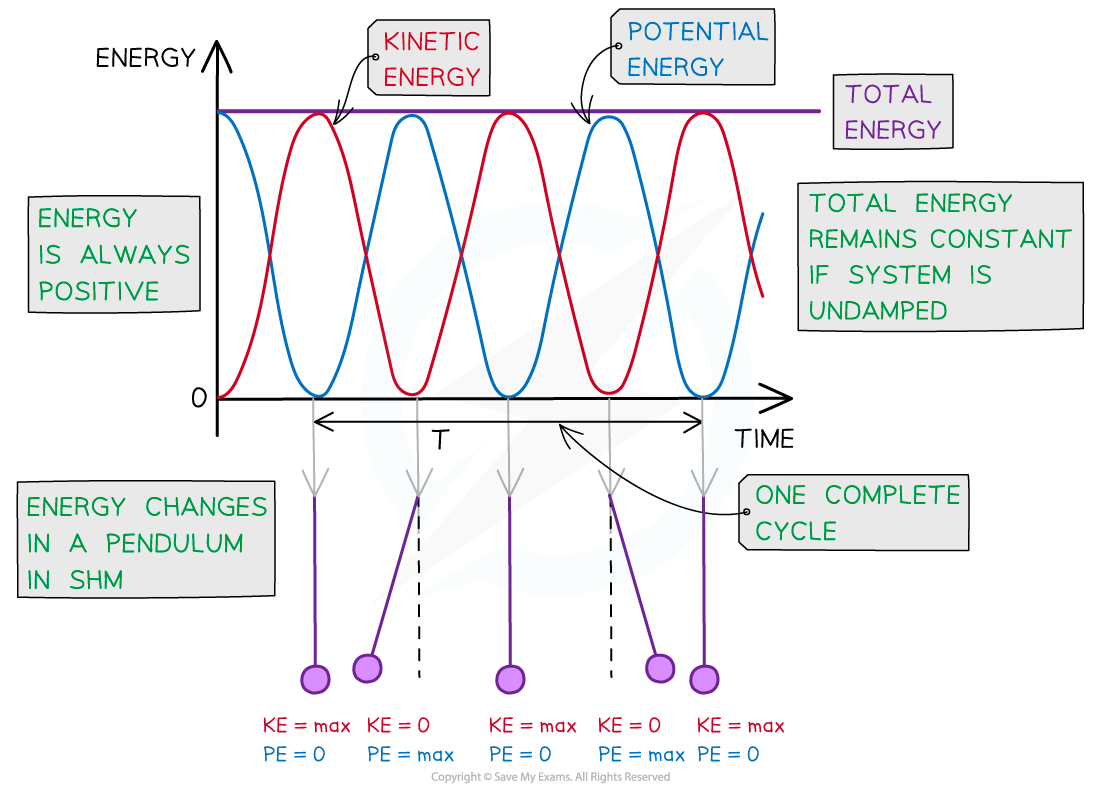
The kinetic and potential energy of an oscillator in SHM vary periodically
The key features of the energy-time graph are:
Both the kinetic and potential energies are represented by periodic functions (sine or cosine) which are varying in opposite directions to one another
When the potential energy is 0, the kinetic energy is at its maximum point and vice versa
The total energy is represented by a horizontal straight line directly above the curves at the maximum value of both the kinetic or potential energy
Energy is always positive so there are no negative values on the y axis
Note: kinetic and potential energy go through two complete cycles during one period of oscillation
This is because one complete oscillation reaches the maximum displacement twice (positive and negative)
Energy-Displacement Graphs
The total energy of system undergoing simple harmonic motion is defined by:
Where:
E = total energy of a simple harmonic system (J)
m = mass of the oscillator (kg)
⍵ = angular frequency (rad s-1)
x0 = amplitude (m)
The energy-displacement graph for half a cycle looks like:
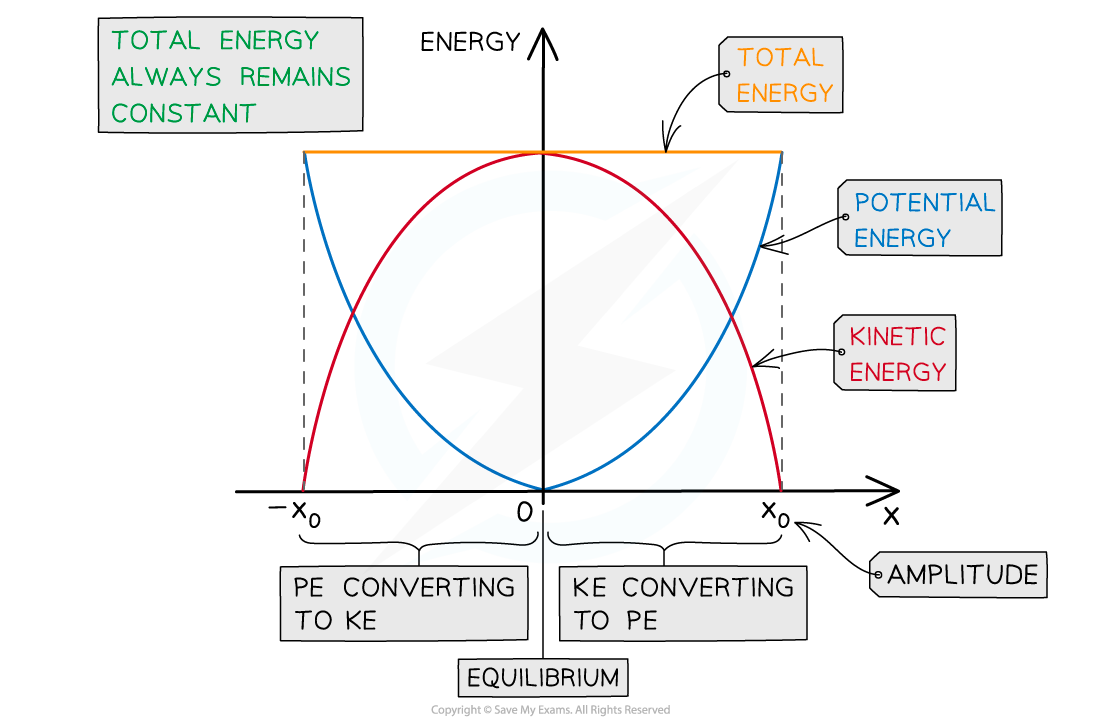
Potential and kinetic energy v displacement in half a period of an SHM oscillation
The key features of the energy-displacement graph:
Displacement is a vector, so, the graph has both positive and negative x values
The potential energy is always at a maximum at the amplitude positions x0 and 0 at the equilibrium position (x = 0)
This is represented by a ‘U’ shaped curve
The kinetic energy is the opposite: it is 0 at the amplitude positions x0 and maximum at the equilibrium position x = 0
This is represented by a ‘n’ shaped curve
The total energy is represented by a horizontal straight line above the curves
Worked Example
A ball of mass 23 g is held between two fixed points A and B by two stretch helical springs, as shown in the figure below

The ball oscillates along the line AB with simple harmonic motion of frequency 4.8 Hz and amplitude 1.5 cm. Calculate the total energy of the oscillations.
Answer:
Step 1: Write down all known quantities
Mass, m = 23 g = 23 × 10–3 kg
Amplitude, x0 = 1.5 cm = 0.015 m
Frequency, f = 4.8 Hz
Step 2: Write down the equation for the total energy of SHM oscillations:
Step 3: Write an expression for the angular frequency
Step 4: Substitute values into energy equation
E = 2.354 × 10–3 = 2.4 mJ
Examiner Tips and Tricks
You may be expected to draw as well as interpret energy graphs against time or displacement in exam questions. Make sure the sketches of the curves are as even as possible and use a ruler to draw straight lines, for example, to represent the total energy.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?