Circular Orbits in Gravitational Fields (OCR A Level Physics): Revision Note
Exam code: H556
Centripetal Force on a Planet
Typically, most planets and satellites have a near circular orbit
Therefore, the gravitational force F between the Sun and another planet provides the centripetal force needed to stay in an orbit
Since the gravitational force is centripetal, it is perpendicular to the direction of travel of the planet
Consider a satellite with mass m orbiting the Earth, with mass M, at a distance r from its centre and travelling with linear speed v
The gravitational force F on the satellite is centripetal, therefore:
F = Fcentripetal
Equating the gravitational force to the centripetal force for a planet or satellite in orbit gives:
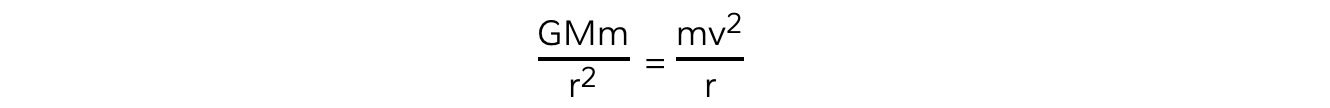
The mass of the satellite m will cancel out on both sides to give:
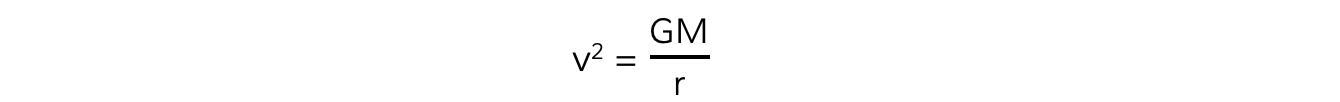
This can be reduced to give an equation for the orbital speed v, as:
Where:
v = orbital speed of the mass in orbit (m s-1)
G = Newton's Gravitational Constant
M = mass of the object being orbited (kg)
r = orbital radius (m)
This means that all satellites, whatever their mass, will travel at the same speed v in a particular orbit radius r
Since the direction of a planet orbiting in circular motion is constantly changing, it has centripetal acceleration
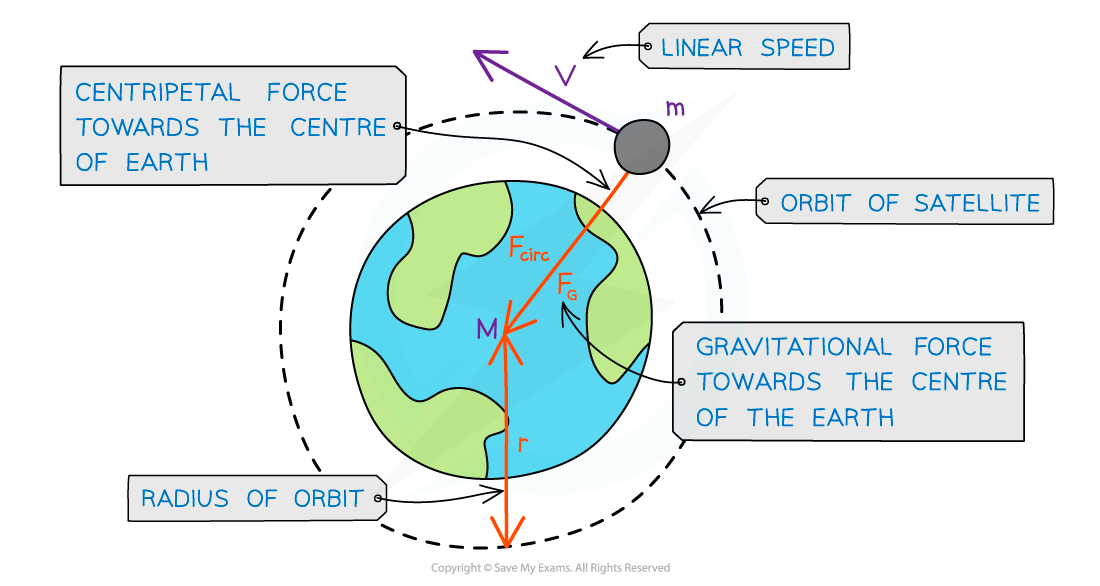
A satellite in orbit around the Earth travels in circular motion
Circular Orbits in Gravitational Fields
Assuming a planet or a satellite is travelling in circular motion when in orbit, its orbital speed v is given by the distance travelled divided by the orbital period T:
This is a result of the well-known equation, speed = distance / time
Where the distance is equal to the circumference of a circle = 2πr
Recall, orbital speed v is also given by:
Therefore:
Expanding the brackets gives:
Rearranging for T2 gives the mathematical expression of Kepler's Third Law which relates the time period T and orbital radius r as:
Where:
T = time period of the orbit, or "orbital period" (s)
r = orbital radius (m)
G = Newton's Gravitational Constant
M = mass of the object being orbited (kg)
Worked Example
A binary star system constant of two stars orbiting about a fixed point B.
The star of mass M1 has a circular orbit of radius R1 and mass M2 also has a circular orbit of radius of R2. Both have linear
speed v and an angular speed ⍵ about B.

State the following formula, in terms of G, M2, R1 and R2
(i) The angular speed ⍵ of M1
(ii) The time period T for each star in terms of angular speed ⍵
Answer:
Part (i)
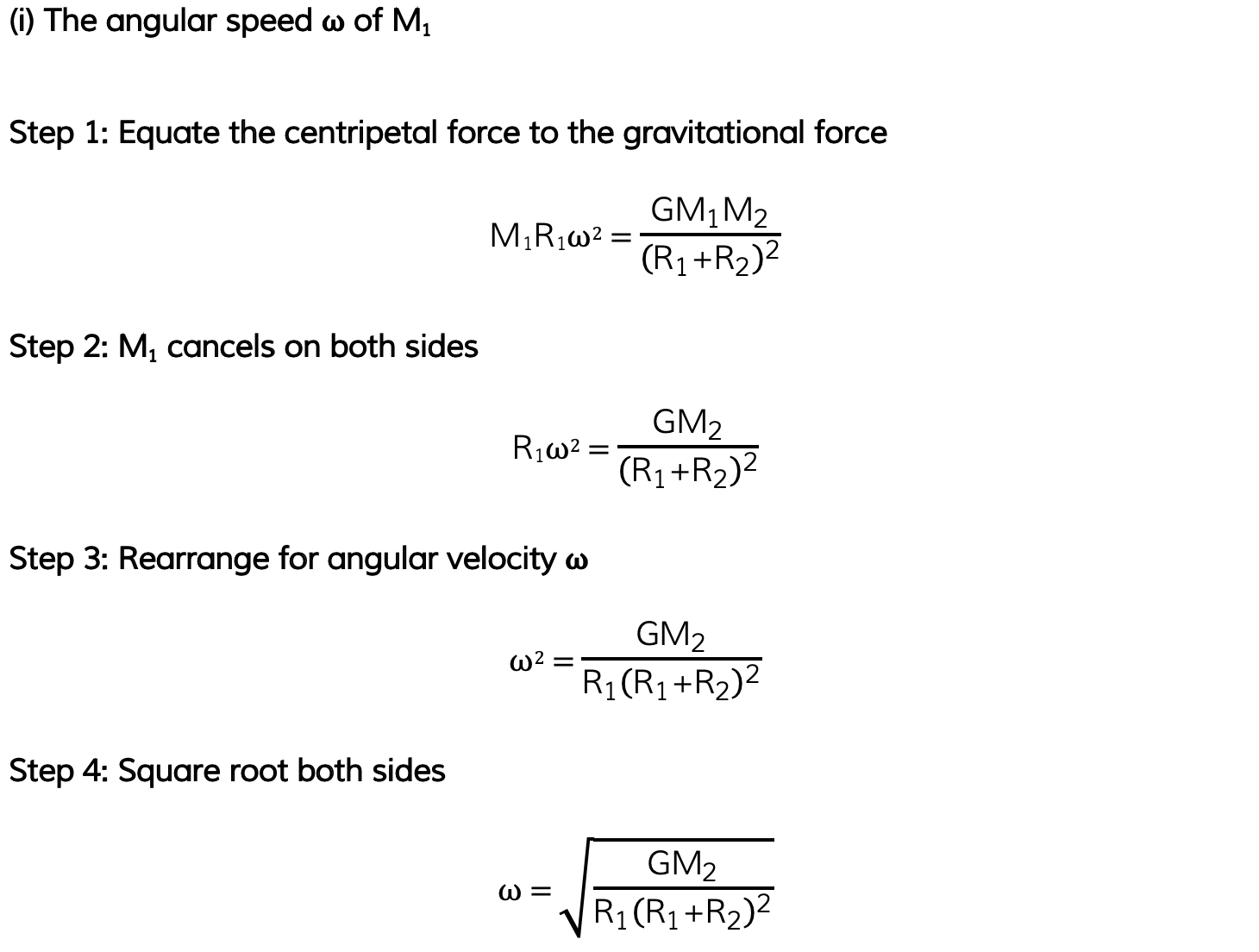
Part (ii)
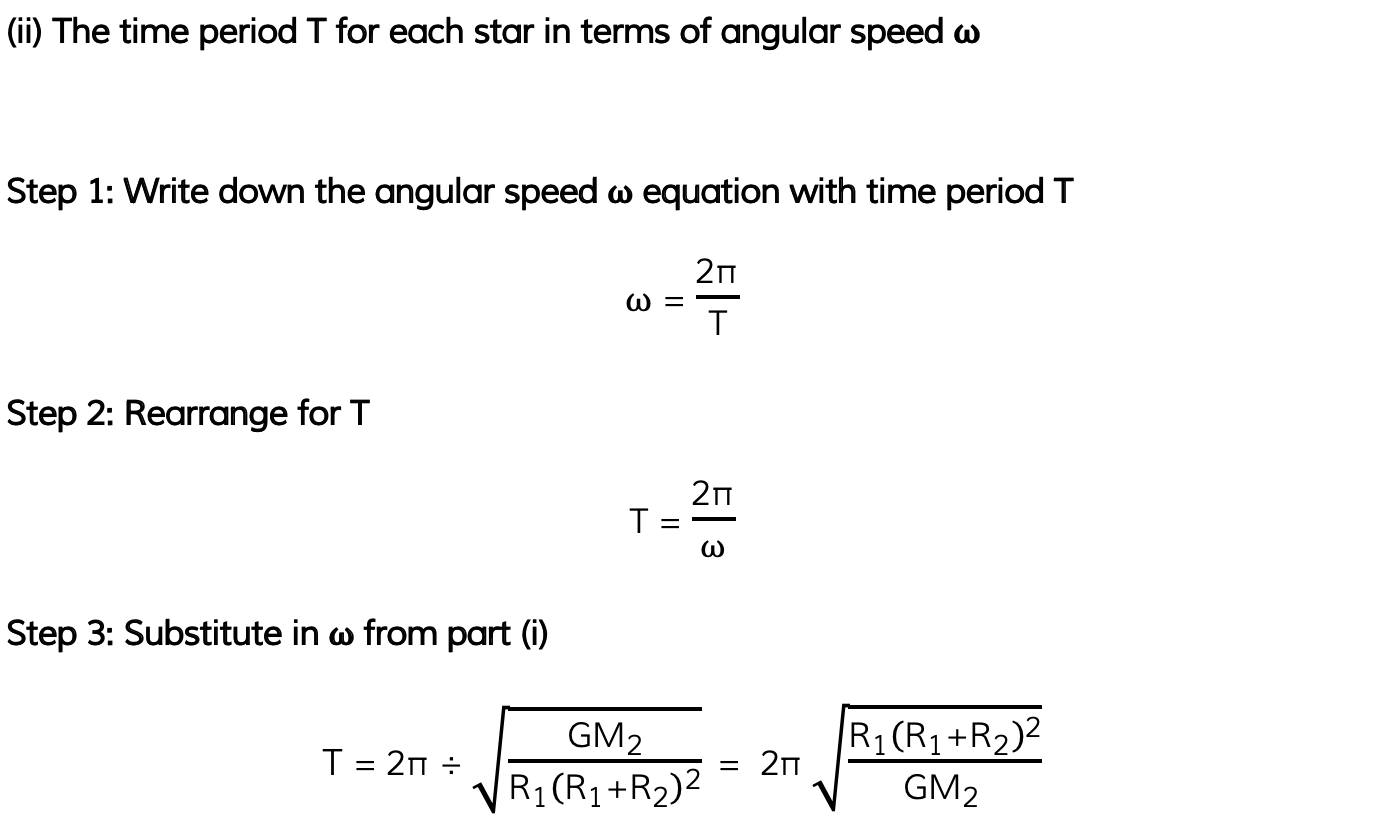
Examiner Tips and Tricks
Many of the calculations in planetary motion questions depend on the equations for circular motion. Be sure to revisit these and understand how to use them! You will be expected to remember the derivation for , so make sure you understand each step, especially equating the gravitational force and the centripetal force!

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?