Gravitational Potential Energy (OCR A Level Physics): Revision Note
Exam code: H556
Gravitational Potential Energy
The gravitational potential Vg at a point is given by:
Recall that potential V is defined as the energy required to bring unit mass m from infinity to a defined point in the field
Recall that the gravitational field is usually caused by 'big mass', M
Therefore, the potential energy E is given by:
E = mVg
Substituting the equation for gravitational potential Vg gives the equation for the gravitational potential energy E between two masses M and m:
Where:
G = Universal Gravitational Constant (N m2 kg–2)
M = mass causing the field (kg)
m = mass moving within the field of M (kg)
r = distance between the centre of m and M (m)
Calculating Changes in Gravitational Potential Energy
When a mass is moved against the force of gravity, work is required
This is because gravity is attractive, therefore, energy is needed to work against this attractive force
The work done (or energy transferred) ∆W to move a mass m between two different points in a gravitational potential ∆V is given by:
∆W = m ∆V
Where:
∆W = work done or energy transferred (J)
m = mass (kg)
∆V = change in gravitational potential (J kg-1)
This work done, or energy transferred, is the change in gravitational potential energy (G.P.E) of the mass
When ∆V = 0, then the the change in G.P.E = 0
The change in G.P.E, or work done, for an object of mass m at a distance r1 from the centre of a larger mass M, to a distance of r2 further away can be written as:

Where:
M = mass that is producing the gravitational field (e.g., a planet) (kg)
m = mass that is moving in the gravitational field (e.g., a satellite) (kg)
r1 = initial distance of m from the centre of M (m)
r2 = final distance of m from the centre of M (m)
Work is done when an object in a planet's gravitational field moves against the gravitational field lines, i.e., away from the planet
This is, again, because gravity is attractive
Therefore, energy is required to move against gravitational field lines
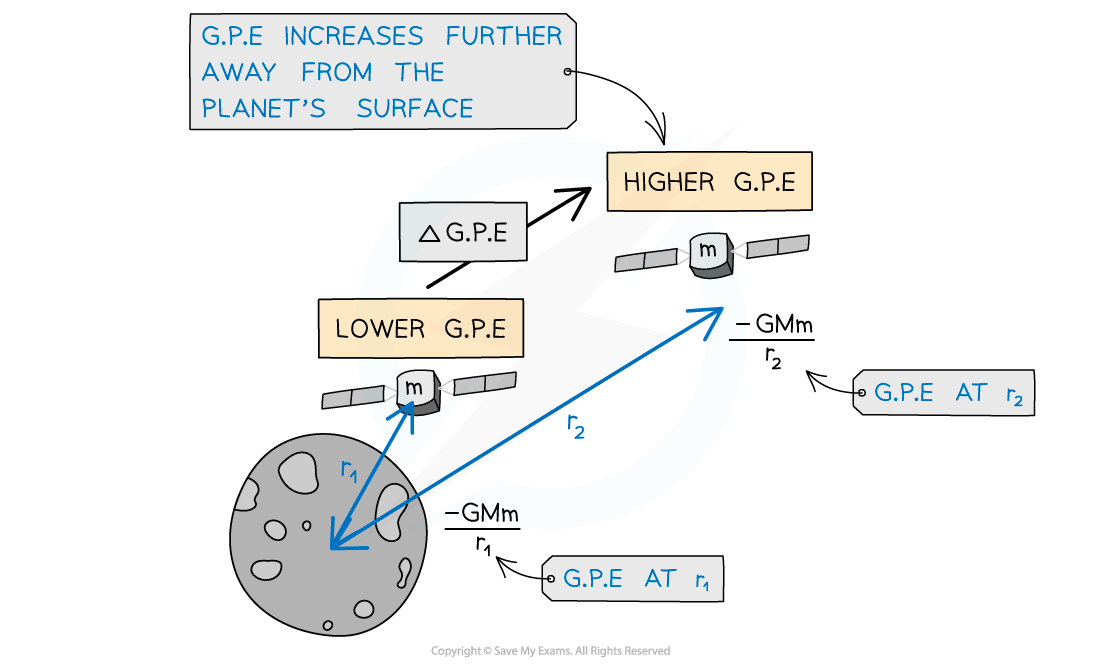
Gravitational potential energy increases as a satellite leaves the surface of the Moon
Worked Example
A spacecraft of mass 300 kg leaves the surface of Mars to an altitude of 700 km. Calculate the work done by the spacecraft.
Radius of Mars = 3400 km
Mass of Mars = 6.40 × 1023 kg
Answer:
Step 1: Write down the work done (or change in G.P.E) equation
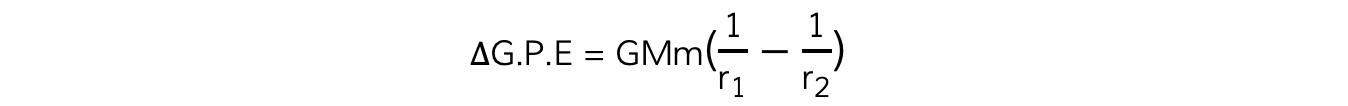
Step 2: Determine values for r1 and r2
r1 is the radius of Mars = 3400 km = 3400 × 103 m
r2 is the radius + altitude = 3400 + 700 = 4100 km = 4100 × 103 m
Step 3: Substitute in values
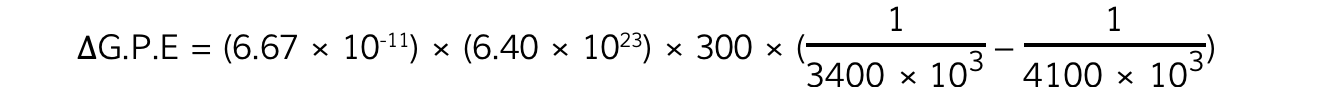
ΔG.P.E = 643.076 × 106 = 640 MJ (2 s.f.)
Examiner Tips and Tricks
Make sure to not confuse the ΔG.P.E equation with
ΔG.P.E = mgΔh
The above equation is only relevant for an object lifted in a uniform gravitational field (close to the Earth’s surface). The new equation for G.P.E will not include g, because this varies for different planets and is no longer a constant (decreases by 1/r2) outside the surface of a planet.
Ready to test your students on this topic?
- Create exam-aligned tests in minutes
- Differentiate easily with tiered difficulty
- Trusted for all assessment types

Did this page help you?