Velocity Selector (OCR A Level Physics): Revision Note
Exam code: H556
Charged Particles in a Velocity Selector
A velocity selector is defined as:
A device consisting of perpendicular electric and magnetic fields where charged particles with a specific velocity can be filtered
Velocity selectors are used in devices, such as mass spectrometers, in order to produce a beam of charged particles all travelling at the same velocity
The construction of a velocity selector consists of two horizontal oppositely charged plates situated in a vacuum chamber
The plates provide a uniform electric field with strength E between them
There is also a uniform magnetic field with flux density B applied perpendicular to the electric field
If a beam of charged particles enter between the plates, they may all have the same charge but travel at different speeds v
The electric force does not depend on the velocity: FE = EQ
However, the magnetic force does depend on the velocity: FB = BQv
The magnetic force will be greater for particles which are travelling faster
To select particles travelling at exactly the desired the speed v, the electric and magnetic force must therefore be equal, but in opposite directions
FE = FB
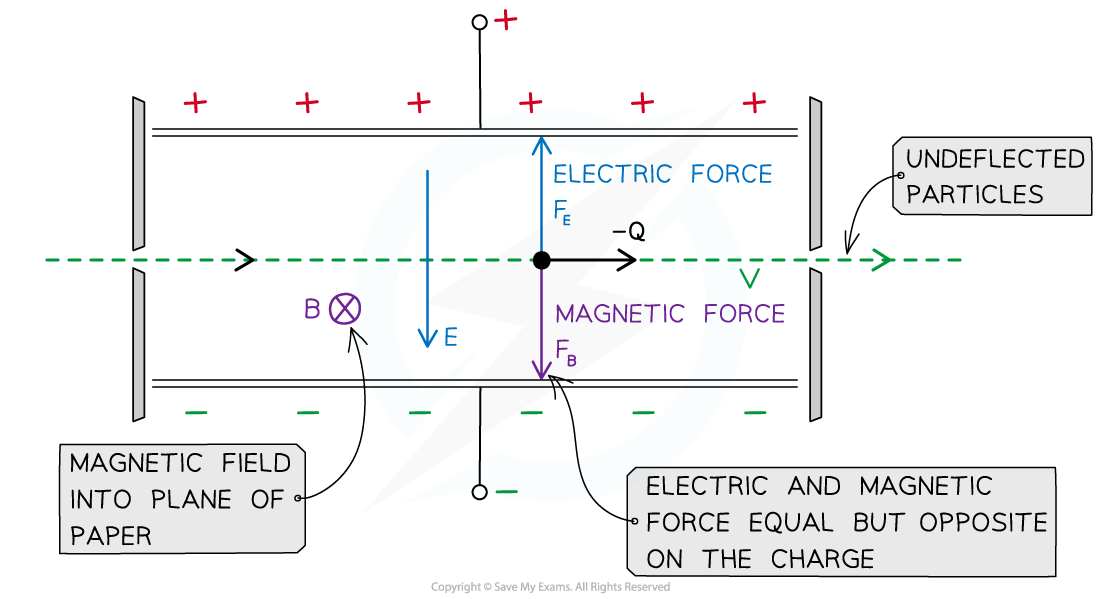
The particles travelling at the desired speed v will travel through undeflected due to the equal and opposite electric and magnetic forces on them
The resultant force on the particles at speed v will be zero, so they will remain undeflected and pass straight through between the plates
By equating the electric and magnetic force equations:
EQ = BQv
The charge Q will cancel out on both sides to give the selected velocity v equation:
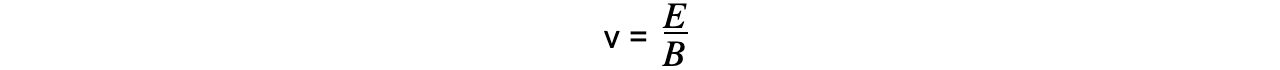
Therefore, the speed v in which a particle will remain undeflected is found by the ratio of the electric and magnetic field strength
If a particle has a speed greater or less than v, the magnetic force will deflect it and collide with one of the charged plates
This would remove the particles in the beam that are not exactly at speed v
Note: the gravitational force on the charged particles will be negligible compared to the electric and magnetic forces and therefore can be ignored in these calculations
Worked Example
A positive ion travels between two charged plates towards a slit S.

a) State the direction of the electric and magnetic fields on the ion.
b) Calculate the speed of the ion emerging from slit S when the magnetic flux density is 0.50 T and the electric field strength is 2.8 kV m−1.
c) Determine which plate the ion will be deflected towards if the speed is greater than the speed in part (b).
Answer:
Part (a)
Step 1: Determine the direction of the E field
Electric field lines point from the positive to negative to charge
Therefore, it must be directed vertically upwards
Step 2: Determine the direction of the B field
Using Fleming’s left-hand rule:
The charge or current I is directed to the right
B must be directed out of the page / screen for the magnetic force F to act vertically downwards
Part (b)
Step 1: List the known quantities
Electric field strength, E = 2.8 kV m−1 = 2.8 × 103 V m−1
Magnetic flux density, B = 0.50 T
Step 2: Write down the velocity selector equation
Step 3: Calculate the speed of the ion at S
= 5600 m s−1
Part (c)
Step 1: Consider the effect of changing the ion's speed on the electric and magnetic forces
Electric force is given by:
FE = EQ
Therefore, electric force does not depend on the velocity
Magnetic force is given by:
FB = BQv
Therefore, FB ∝ v, so if the speed increases, the magnetic force must increase
Step 2: Determine the net direction of the force
Since the net magnetic force would direct the ion downwards in the direction of the field
The ion will be deflected towards the positive plate

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?