Magnetic Flux (OCR A Level Physics): Revision Note
Exam code: H556
Magnetic Flux
Magnetic flux is a quantity which signifies how much of a magnetic field passes perpendicularly through an area
For example, the amount of magnetic flux through a rotating coil will vary as the coil rotates in the magnetic field
It is a maximum when the magnetic field lines are perpendicular to the coil area
It is at a minimum when the magnetic field lines are parallel to the coil area
The magnetic flux is defined as:
The product of the magnetic flux density and the cross-sectional area perpendicular to the direction of the magnetic flux density
Magnetic flux is defined by the symbol
(greek letter ‘phi’)
It is measured in units of Webers (Wb)
Magnetic flux can be calculated using the equation:
Where:
Φ = magnetic flux (Wb)
B = magnetic flux density (T)
A = cross-sectional area (m2)
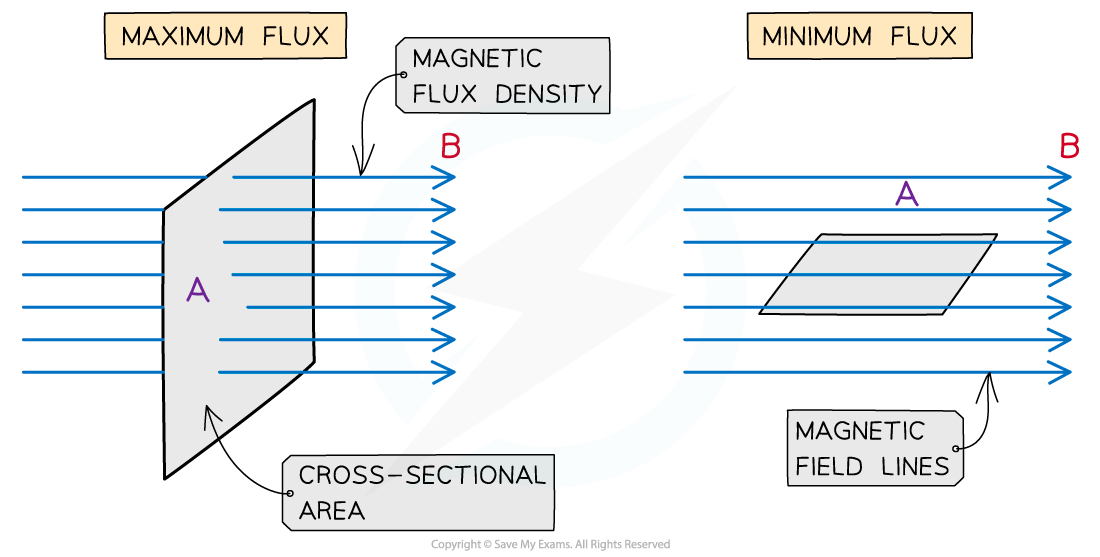
The magnetic flux is maximised when the magnetic field lines and the area through which they are passing through are perpendicular
When magnetic flux is not completely perpendicular to the area A, then the component of magnetic flux density B perpendicular to the area is taken
The equation then becomes:
Where:
θ = angle between magnetic field lines and the line perpendicular to the plane of the area (often called the normal line) (degrees)
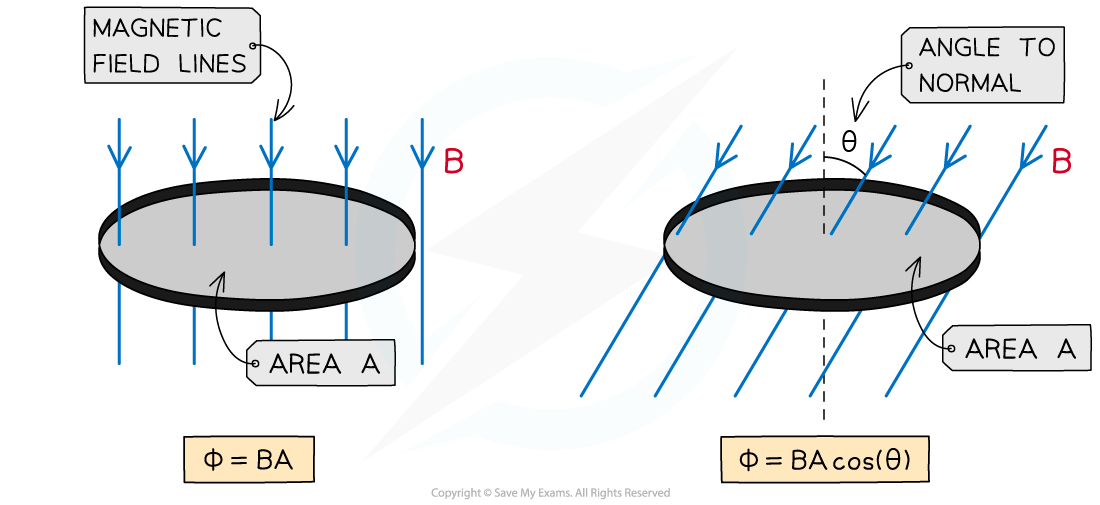
The magnetic flux increases as the angle between the field lines and plane decreases
This means the magnetic flux is:
Maximum = BA when cos(θ) =1 therefore θ = 0o. The magnetic field lines are perpendicular to the plane of the area
Minimum = 0 when cos(θ) = 0 therefore θ = 90o. The magnetic fields lines are parallel to the plane of the area
An e.m.f is induced in a circuit when the magnetic flux linkage changes with respect to time
This means an e.m.f is induced when there is:
A changing magnetic flux density B
A changing cross-sectional area A
A change in angle θ
Worked Example
An aluminium window frame has a width of 40 cm and length of 73 cm as shown in the figure below

The frame is hinged along the vertical edge AC. When the window is closed, the frame is normal to the Earth’s magnetic field with magnetic flux density 1.8 × 10−5 T
a) Calculate the magnetic flux through the window when it is closed
b) Sketch the graph of the magnetic flux against angle between the field lines and the normal when the window is opened and rotated by 180°
Answer:
Part (a)
Step 1: Write out the known quantities
Cross-sectional area, A = 40 cm × 73 cm = (40 × 10−2) × (73 × 10−2) = 0.292 m2
Magnetic flux density, B = 1.8 × 10−5 T
Step 2: Write down the equation for magnetic flux
Φ = BA
Step 3: Substitute in values
Φ = (1.8 × 10−5) × 0.292 = 5.256 × 10−6 = 5.3 × 10−6 Wb
Part (b)
The magnetic flux will be at a minimum when the window is opened by 90°
The magnetic flux will be at a maximum when fully closed or opened to 180°

Examiner Tips and Tricks
Consider carefully the value of θ, it is the angle between the field lines and the line normal (perpendicular) to the plane of the area the field lines are passing through.
If it helps you, drawing the normal on the area provided is a helpful way to visualise the correct angle.
Investigating Magnetic Flux
Aims of the Experiment
The overall aim of this experiment is to determine how the magnetic flux linkage varies with the angle of rotation of a search coil
This is done by rotating a search coil through a uniform magnetic field created by a larger coil and recording the induced e.m.f. within it
Variables
Independent variable = Angle between the normal to the search coil and the magnetic field lines, θ
Dependent variable= Induced e.m.f, ε
Control variables:
Area of the search coil, A
Number of loops on both coils, N
Magnetic field strength, B
Frequency of the power supply, f
Equipment List

Resolution of measuring equipment:
Protractor = 1º
CRO = 2 mV / div
Method
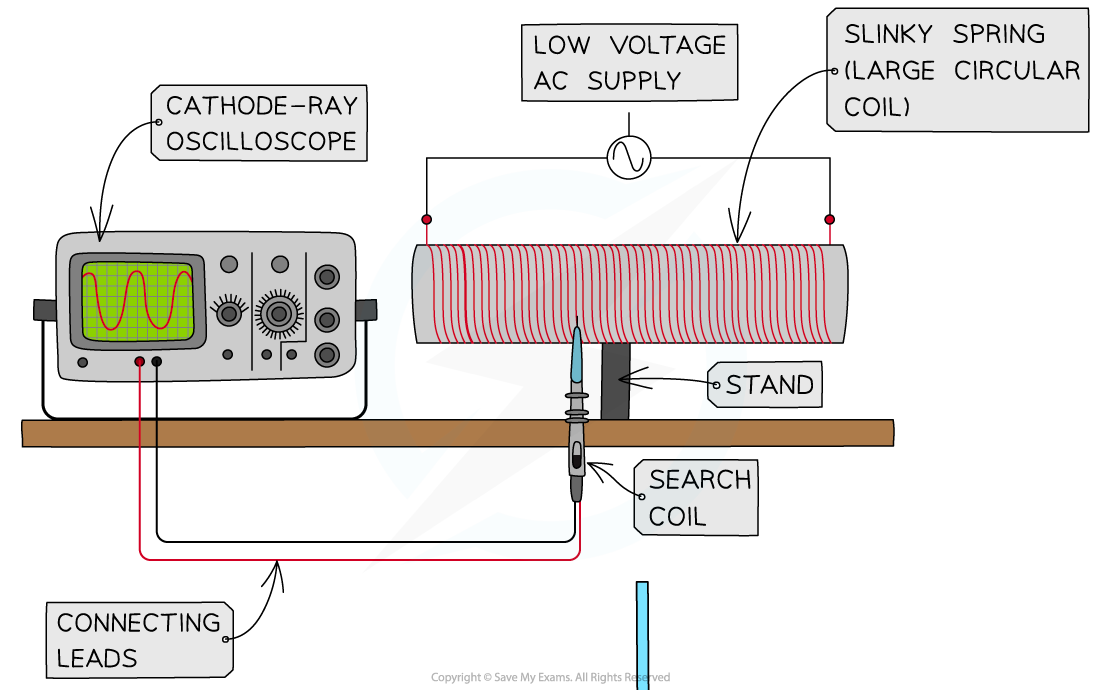
Arrange the apparatus as shown in the diagram.
The slinky spring should be connected to the alternating power supply so the flux through the search coil placed within it will be constantly changing
Set up the CRO so its time-base is switched off, so it only shows the amplitude of the e.m.f.
Adjust the voltage per division till the signal can be seen fully on the screen (eg. 10 mV / div)
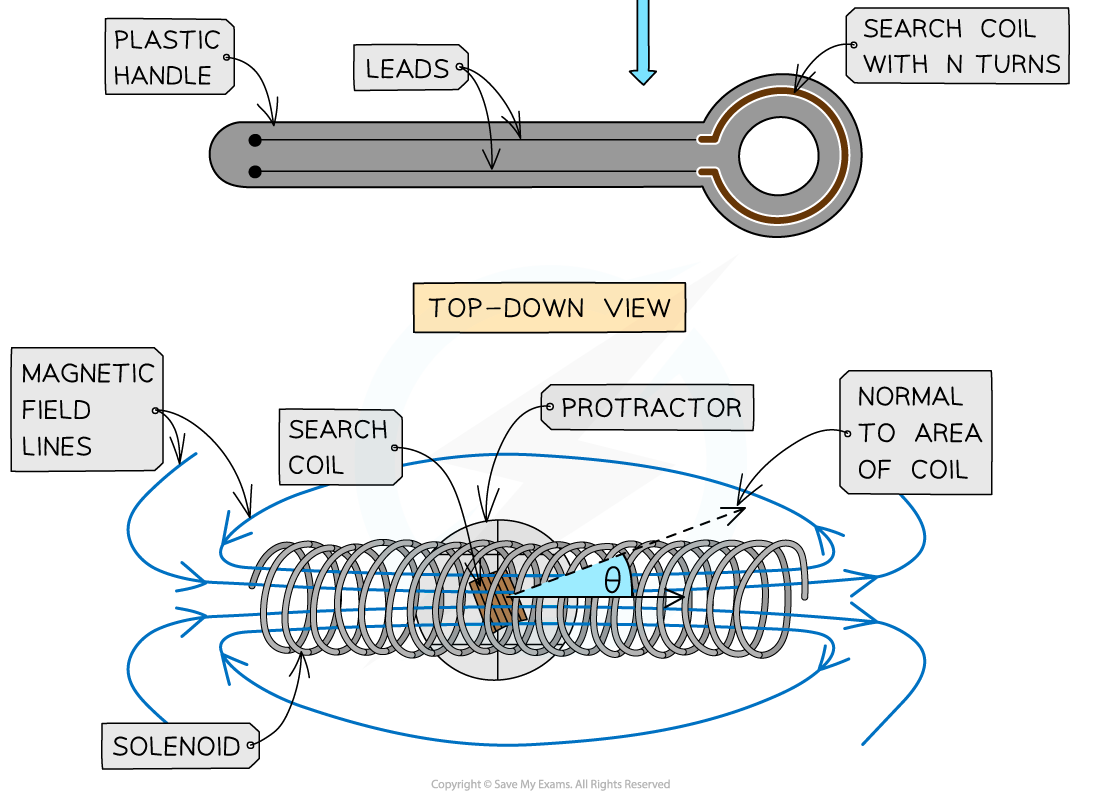
Position the search coil so that it is halfway along the slinky spring
Orient the search coil so it is parallel to the slinky spring
The plane of its area is perpendicular to the field)
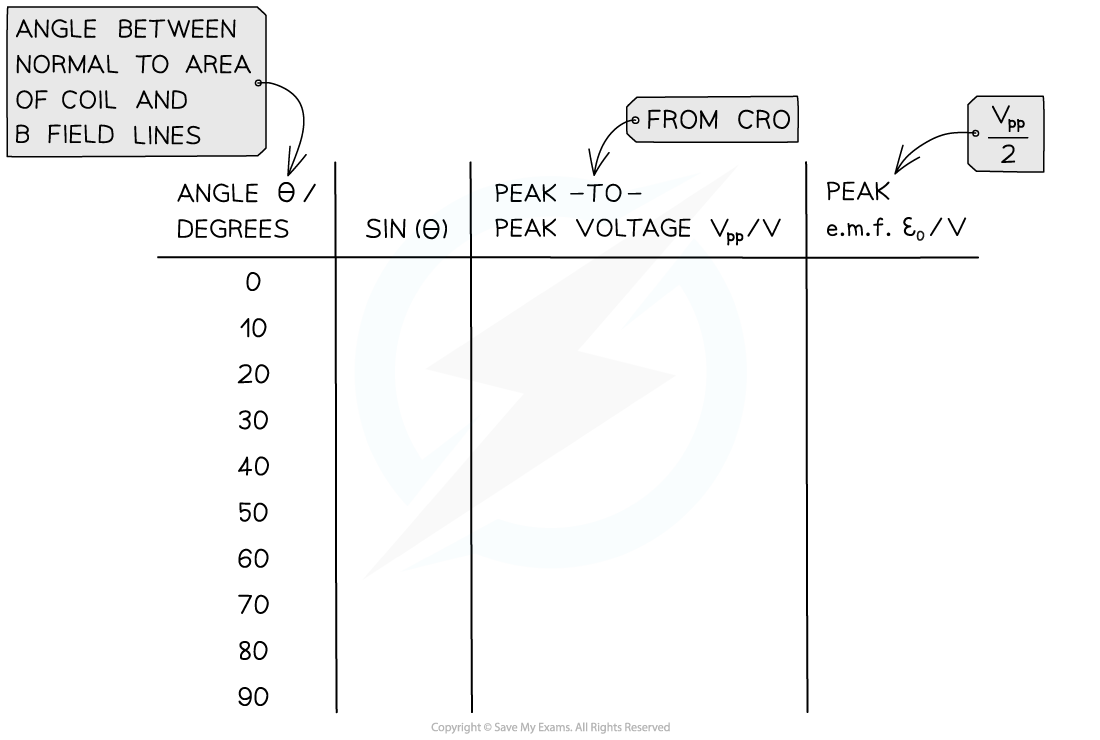
Record the induced e.m.f. in the search coil from the amplitude of the CRO trace
This should ideally be the peak-to-peak voltage (Vpp) which will then be halved for the peak e.m.f, ε0
Rotate the search coil by 10º (in either direction) using the protractor
Record the new Vpp and repeat the procedure until the search coil is at 90º to the slinky spring
An example table might look like this:
Analysing the Results
The e.m.f. in the coil varies with the equation:
ε = BANω sin(θ)
Where:
ε = e.m.f. (V)
B = magnetic flux density (T)
A = cross-sectional area (m2)
N = number of turns
ω = angular velocity of the rotating coil (rad s−1 or degrees s−1 )
θ = angle between the magnetic field, B and the normal to the area, A (rads)
Comparing this to the straight-line equation: y = mx + c
y = ε
x = sin(θ)
m = BANω
c = 0
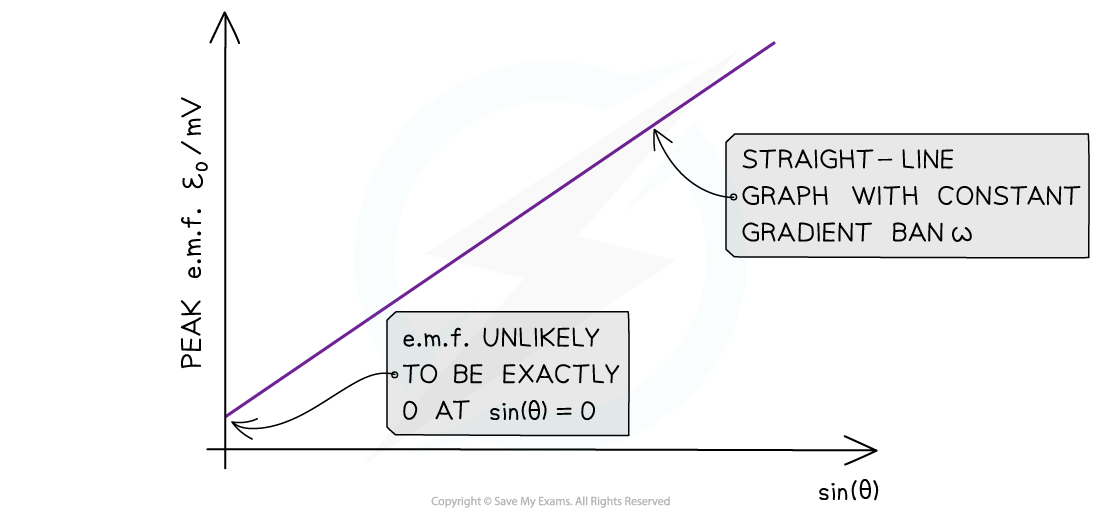
Plot a graph of peak e.m.f. ε0 against sin(θ) and draw a line of best fit
This should be a straight-line graph
This shows that the induced e.m.f. is proportional to the cosine of the angle between the search coil and the direction of the magnetic field lines
Evaluating the Experiment
Systematic Errors:
Reduce systematic errors by calibrating the search coil using a known magnetic field and oscilloscope
The field lines are unlikely to be perfectly parallel and perpendicular to the area of the coil
Therefore, the graph is unlikely to have a y-intercept at the origin
Read the angle from the protractor far above and from the same point every time to reduce parallax error
Random Errors:
The experiment could be made more reliable by repeating for a full turn (θ = 360°)
An improvement could be to use a calibrated motor to rotate the search coil at a steady rate
This will make the e.m.f. values more accurate
Use blu tack to make sure the protractor stays in the same place for each reading
Safety Considerations
Keep water or any fluids away from the electrical equipment
Make sure no wires or connections are damaged and contain appropriate fuses to avoid a short circuit or a fire
Don't exceed the specified current rating for the coil in order not to damage it
The larger coil will heat up whilst the current is through it, especially if it is very thin
Therefore, make sure not to leave the current on for longer than necessary

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?