Calculating Induced E.m.f (OCR A Level Physics): Revision Note
Exam code: H556
Calculating Induced E.m.f.
Combining Lenz's Law into the equation for Faraday's Law is written as:
Where
ε = induced e.m.f (V)
Δ(Nɸ) = change in flux linkage (Wb turns)
Δt = time interval (s)
The negative sign represents Lenz's Law
This is because it shows the induced e.m.f. ε is set up in an 'opposite direction' to oppose the changing flux linkage
This equation shows that the gradient of a graph of magnetic flux linkage against time, t, represents the magnitude of the induced e.m.f.
Note: the negative sign means that if the gradient is positive, the induced e.m.f. is negative
This is again due to Lenz's law, which says the e.m.f. is set up to oppose the effects of the changing flux linkage
Worked Example
A small rectangular coil contains 350 turns of wire. The longer sides are 3.5 cm and the shorter sides are 1.4 cm.
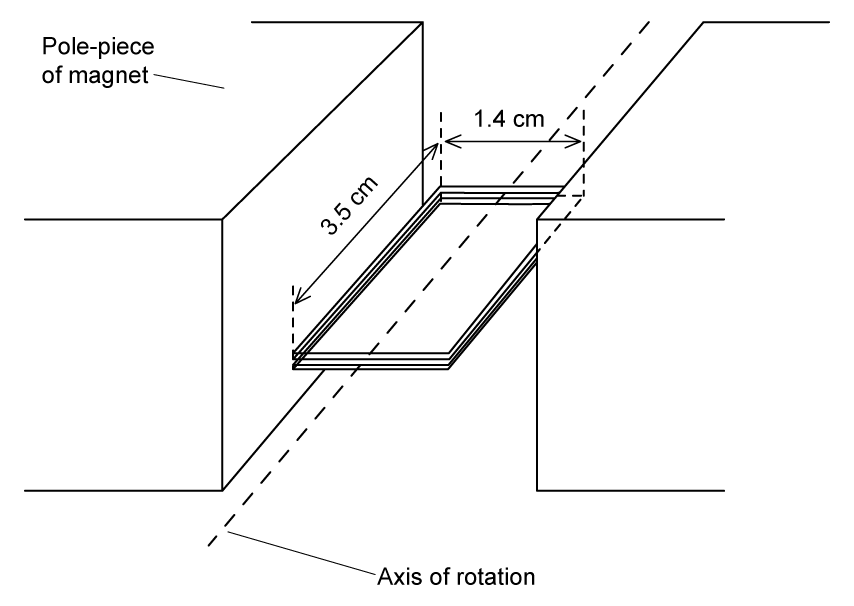
The coil is held between the poles of a large magnet so that it can rotate about an axis through its centre. The magnet produces a uniform magnetic field of flux density 80 mT between its poles.
The coil is positioned horizontally and then turned through an angle of 90° in a time of 0.18 s.
Calculate the magnitude of the average e.m.f. induced in the coil.
Answer:
Step 1: Write down the known quantities
Magnetic flux density, B = 80 mT = 80 × 10-3 T
Area, A = 3.5 × 1.4 = (3.5 × 10-2) × (1.4 × 10-2) = 4.9 × 10-4 m2
Number of turns, N = 350
Time interval, Δt = 0.18 s
Step 2: Write out the equation for Faraday’s law:
Step 3: Write out the equation for the change in flux linkage:
The number of turns N and the coil area A stay constant
The flux through the coil changes as it rotates
Therefore, the change in flux linkage can be written as:
Step 4: Determine the change in magnetic flux linkage
The initial flux through the coil is zero (flux lines are parallel to the coil face)
The final flux through the coil is 80 mT (flux lines are perpendicular to the coil face)
This is because the coil begins horizontally in the field and is rotated 90°
Therefore, the change in flux linkage is:
= 350 × (4.9 × 10-4) × (80 × 10-3) = 0.014 Wb turns
Step 5: Substitute change in flux linkage and time into Faraday’s law equation:
= 0.076 V
EMF Induced in a Rotating Coil
When a coil rotates in a uniform magnetic field, the flux through the coil will vary as it rotates
Since e.m.f is the rate of change of flux linkage, this means the e.m.f will also change as it rotates
The maximum e.m.f is when the coil cuts through the most field lines
The e.m.f induced is an alternating voltage
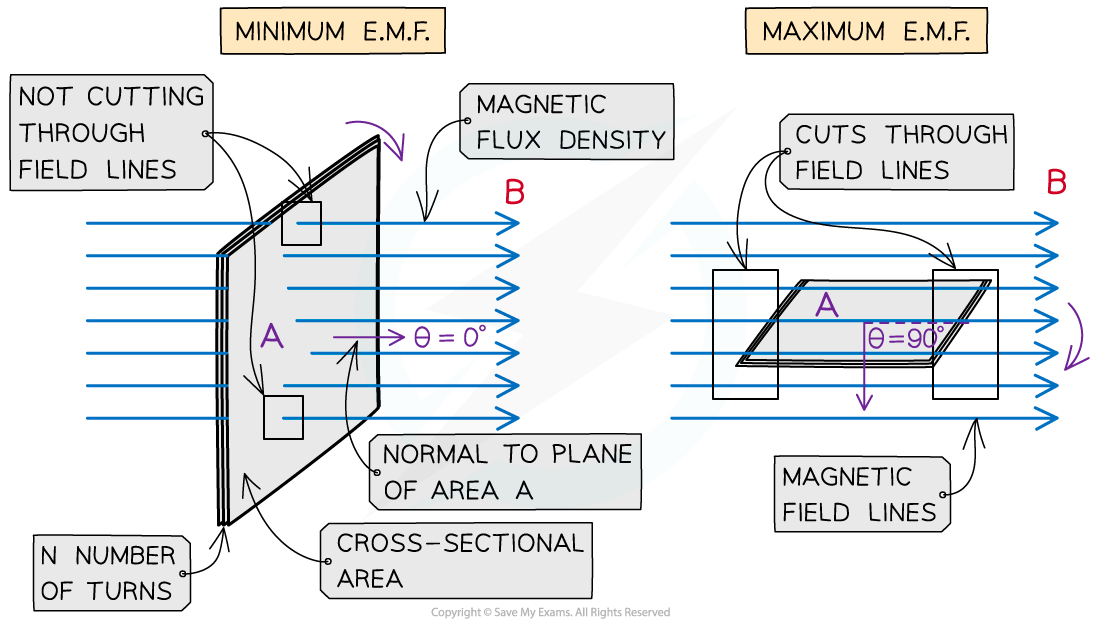
The maximum e.m.f is when the coil cuts through the field lines when they are parallel to the plane of the coil
This means that the e.m.f is:
Maximum when θ = 90o. The magnetic field lines are parallel to the plane of the area (or the normal to the area is perpendicular to the field lines)
0 when θ = 0o. The magnetic fields lines are perpendicular to the plane of the area (or the normal to the area is parallel to the field lines)
This is the opposite of the maximum and minimum flux through the coil
The flux linkage can also be written as:
NΦ = BAN cos(θ)
Where the angle θ depends on the angular speed of the coil, ω:
θ = ωt
The induced e.m.f., ε from Faraday's Law depends on the rate of change of flux linkage, which means it can also be written as:
ε = BANω sin(θ)
ε = e.m.f. (V)
B = magnetic flux density (T)
A = cross-sectional area (m2)
N = number of turns
ω = angular velocity of the rotating coil (rad s−1 )
θ = angle between the magnetic field, B and the normal to the area, A (rads)
The equation shows that the e.m.f. varies sinusoidally and it is 90° out of phase with the flux linkage

The e.m.f and flux linkage are 90° out of phase
Worked Example
A rectangular coil was 40 turns, each with an area of 0.5 m2 is rotated at 42 rad s−1 in a uniform 3.15 mT magnetic field.
Calculate the maximum e.m.f. induced in the coil.
Answer:
Step 1: Write the known quantities
Number of turns, N = 40
Area, A = 0.5 m2
Angular velocity, ω = 42 rad s−1
Magnetic flux density, B = 3.15 mT = 3.15 × 10−3 T
Step 2: Write down the e.m.f. equation
ε = BANω sin(ωt)
Step 3: Determine when the maximum e.m.f. will be
The maximum e.m.f. occurs when sin(ωt) = ±1, or when the coil is parallel to the magnetic field
Step 4: Substitute in the values
ε = (3.15 × 10−3) × 0.5 × 40 × 42 × ±1 = ± 2.6 V
Examiner Tips and Tricks
The 'magnitude' of the e.m.f. just means its size, rather than its direction. This is often what is required in exam questions, so the minus sign in Lenz's law is not necessarily required in calculations. However, you may be expected to explain the significance of the negative sign in the equation, so be prepared to interpret it as an expression of Lenz's Law!
Remember that the greek letter delta, 'Δ', simply means 'change in'.
Remember not to get mixed up with when the e.m.f. or the flux linkage is at their maximum:
When the plane of the coil is perpendicular to the field lines
The flux linkage is at its maximum
The e.m.f. = 0
When the plane of the coil is parallel to the field lines
The flux linkage is 0
the e.m.f. is at its maximum
Since ω is in units of rads s−1, make sure your calculator is in radians mode before doing calculations

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?