A LevelPhysicsOCRRevision Notes6. Particles & Medical PhysicsMagnetic FieldsForce on a Current-Carrying Conductor

Force on a Current-Carrying Conductor (OCR A Level Physics): Revision Note

Exam code: H556

Katie M

Author

Katie M

Last updated

Magnetic Flux Density

  • The magnetic flux density B is defined as:

The force acting per unit current per unit length on a current-carrying conductor placed perpendicular to the magnetic field

  • Rearranging the equation for magnetic force on a wire, the magnetic flux density is defined by the equation:

B space equals space fraction numerator F over denominator I L end fraction

  • Where:

    • B = magnetic flux density (T)

    • F = magnetic force (N)

    • I = current (A)

    • L = length of the wire (m)

  • Note: this equation is only relevant when the B-field is perpendicular to the current

  • Magnetic flux density is measured in units of tesla, which is defined as:

A wire carrying a current of 1 A normal to a magnetic field of flux density of 1 T with a force per unit length of the conductor of 1 N m−1

  • To put this into perspective, the Earth's magnetic flux density is around 0.032 mT and an ordinary fridge magnet is around 5 mT

  • The magnetic flux density is sometimes referred to as the magnetic field strength

Worked Example

A 15 cm length of wire is placed vertically and at right angles to a magnetic field. When a current of 3.0 A flows in the wire vertically upwards, a force of 0.04 N acts on it to the left.

Determine the flux density of the field and its direction.

Answer:

Step 1: Write out the known quantities

  • Force on wire, F = 0.04 N

  • Current, I = 3.0 A

  • Length of wire, L = 15 cm = 15 × 10−2 m

Step 2: Write out the magnetic flux density B equation

B space equals space fraction numerator F over denominator I L end fraction

Step 3: Substitute in values

B space equals space fraction numerator 0.04 over denominator 3 cross times open parentheses 15 cross times 10 to the power of negative 2 end exponent close parentheses end fraction space equals space 0.09 space straight T

Step 4: Determine the direction of the B field

  • Using Fleming’s left-hand rule:

    • F = to the left

    • I = vertically downwards (flow of conventional current)

    • therefore, B = out of the page 

Force on a Current-Carrying Conductor

  • A current-carrying conductor produces its own magnetic field

    • An external magnetic field will therefore exert a magnetic force on it

  • A current-carrying conductor (e.g. a wire) will experience the maximum magnetic force if the current through it is perpendicular to the direction of the magnetic flux lines

    • A simple situation would be a copper rod placed within a uniform magnetic field

    • When current is passed through the copper rod, it experiences a force which makes it accelerate

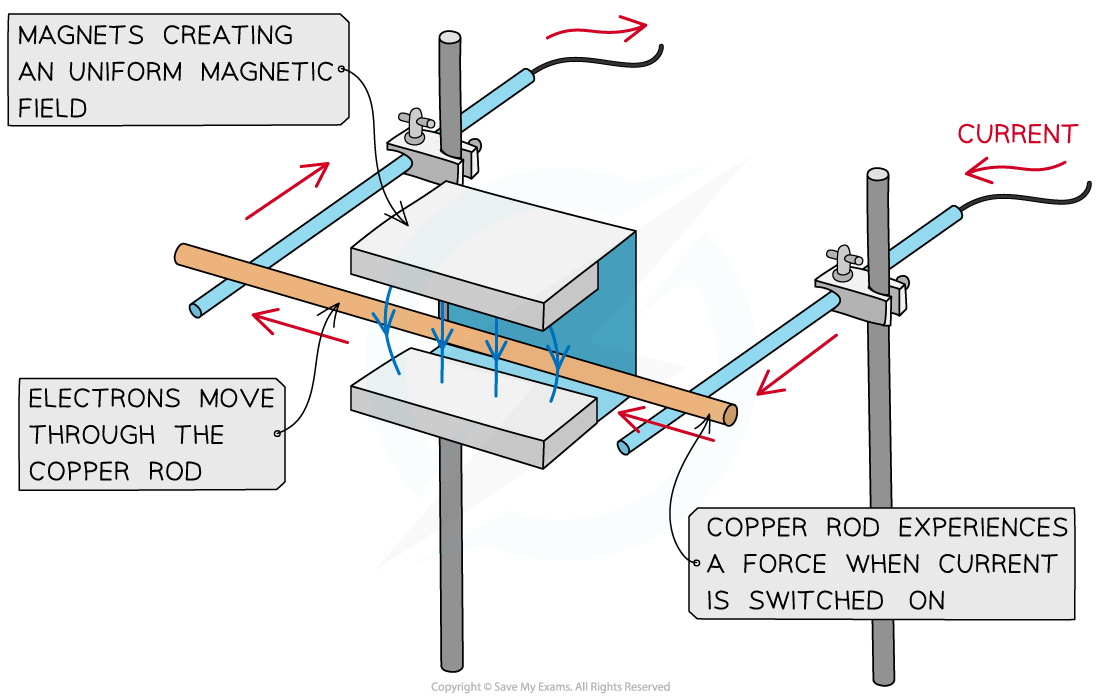
Copper rod experiment, downloadable AS & A Level Physics revision notes

A copper rod moves within a magnetic field when current is passed through it

  • The force F on a conductor carrying current I in a magnetic field with flux density B is defined by the equation:

F space equals space B I L thin space sin space theta

  • Where:

    • F = magnetic force on the current-carrying conductor (N)

    • B = magnetic flux density of external magnetic field (T)

    • I = current in the conductor (A)

    • L = length of the conductor in the field (m)

    • θ = angle between the conductor and external flux lines (degrees)

  • This equation shows that the magnitude of the magnetic force F is proportional to:

    • Current I 

    • Magnetic flux density B

    • Length of conductor in the field L

    • The sine of the angle θ between the conductor and the magnetic flux lines

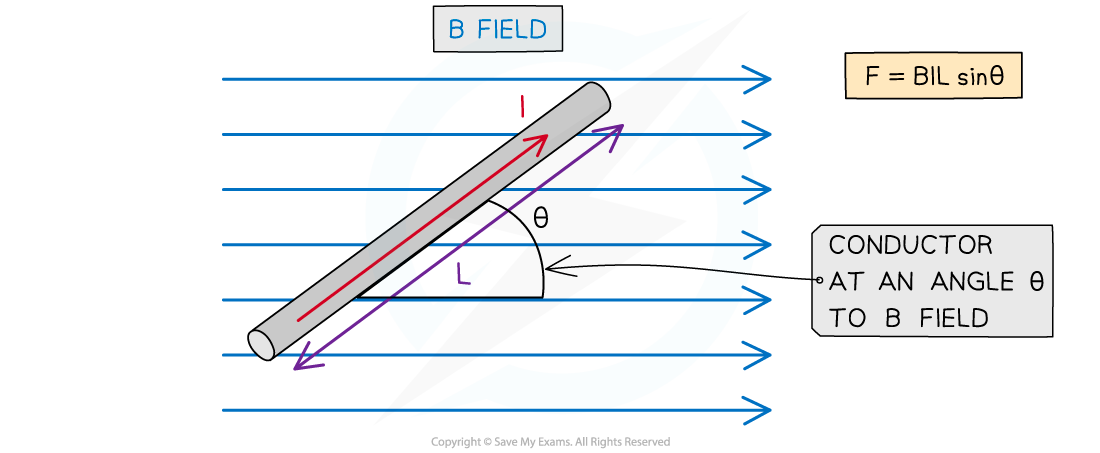
Force on conductor (1), downloadable AS & A Level Physics revision notes
Force on conductor (2), downloadable AS & A Level Physics revision notes

Magnitude of the force on a current carrying conductor depends on the angle of the conductor to the external B field

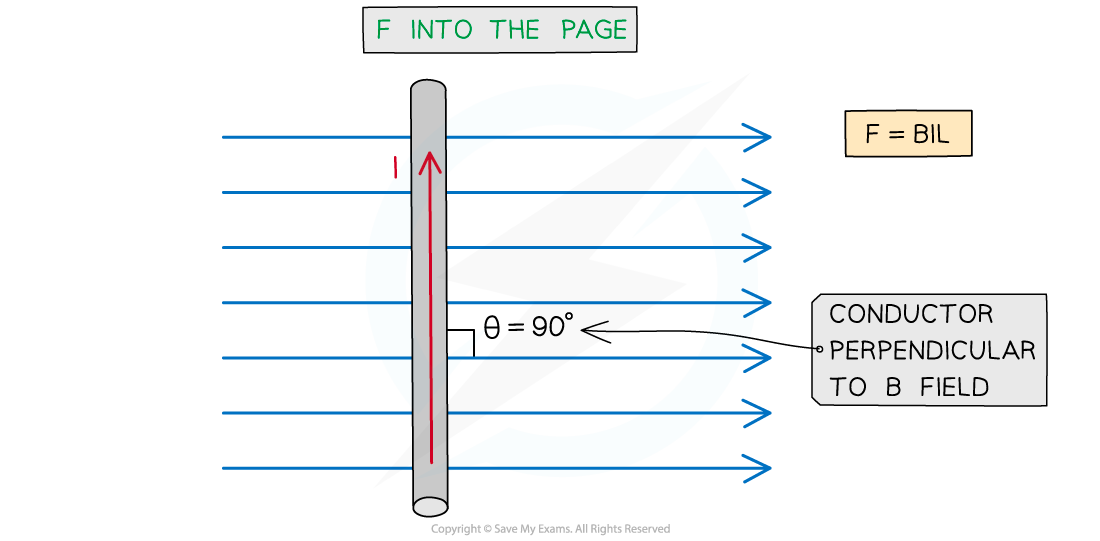
  • The maximum force occurs when sin space theta space equals space 1

    • This means theta space equals space 90 degree and the conductor is perpendicular to the B field

    • This equation for the magnetic force now becomes:

F space equals space B I L

  • The minimum force (0) is when sin space theta space equals space 0

    • This means theta space equals space 0 degree and the conductor is parallel to the B field

  • It is important to note that a current-carrying conductor will experience no force if the current in the conductor is parallel to the field

Worked Example

A current of 0.87 A flows in a wire of length 1.4 m placed at 30o to a magnetic field of flux density 80 mT.

Calculate the force on the wire.

Answer:

Step 1: Write down the known quantities

  • Magnetic flux density, B = 80 mT = 80 × 10−3 T

  • Current, I = 0.87 A

  • Length of wire, L = 1.4 m

  • Angle between the wire and the magnetic flux lines, θ = 30o

Step 2: Write down the equation for the magnetic force on a current-carrying conductor

F space equals space B I L thin space sin space theta

Step 3: Substitute in values and calculate

F space equals space open parentheses 80 cross times 10 to the power of negative 3 end exponent close parentheses open parentheses 0.87 close parentheses open parentheses 1.4 close parentheses thin space sin space 30 degree space equals space 0.049 space straight N

Examiner Tips and Tricks

Remember that the direction of current is the flow of positive charge (i.e. conventional current) and this is opposite to the flow of electrons.

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourself

Did this page help you?

Previous:Fleming's Left-Hand RuleNext:Magnetic Flux Density
Katie M

Author: Katie M

Expertise: Physics Content Creator

Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

Download notes on Force on a Current-Carrying Conductor