Cubic Graphs (Cambridge (CIE) IGCSE International Maths)

Revision Note

Author

Jamie Wood

Expertise

Maths

Cubic Graphs

What is a cubic?

A cubic is a function of the form $a x^{3} + b x^{2} + c x + d$
- $a, b, c$ and $d$ are constants
- It is a polynomial of degree (order) 3
  - So $b, c$ and/or $d$ could be zero
To sketch the graph of a cubic polynomial needs to be in factorised form
- E.g. $(2 x - 1) (x + 2) (x - 3)$ is the factorised form of $2 x^{3} - 3 x^{2} - 11 x + 6$
You do not need to factorise a cubic unless it is a more simple one
- E.g. $x^{3} - 4 x = x (x^{2} - 4) = x (x - 2) (x + 2)$
- You should be able to expand three brackets to find the expanded form of a cubic

What does the graph of a cubic look like?

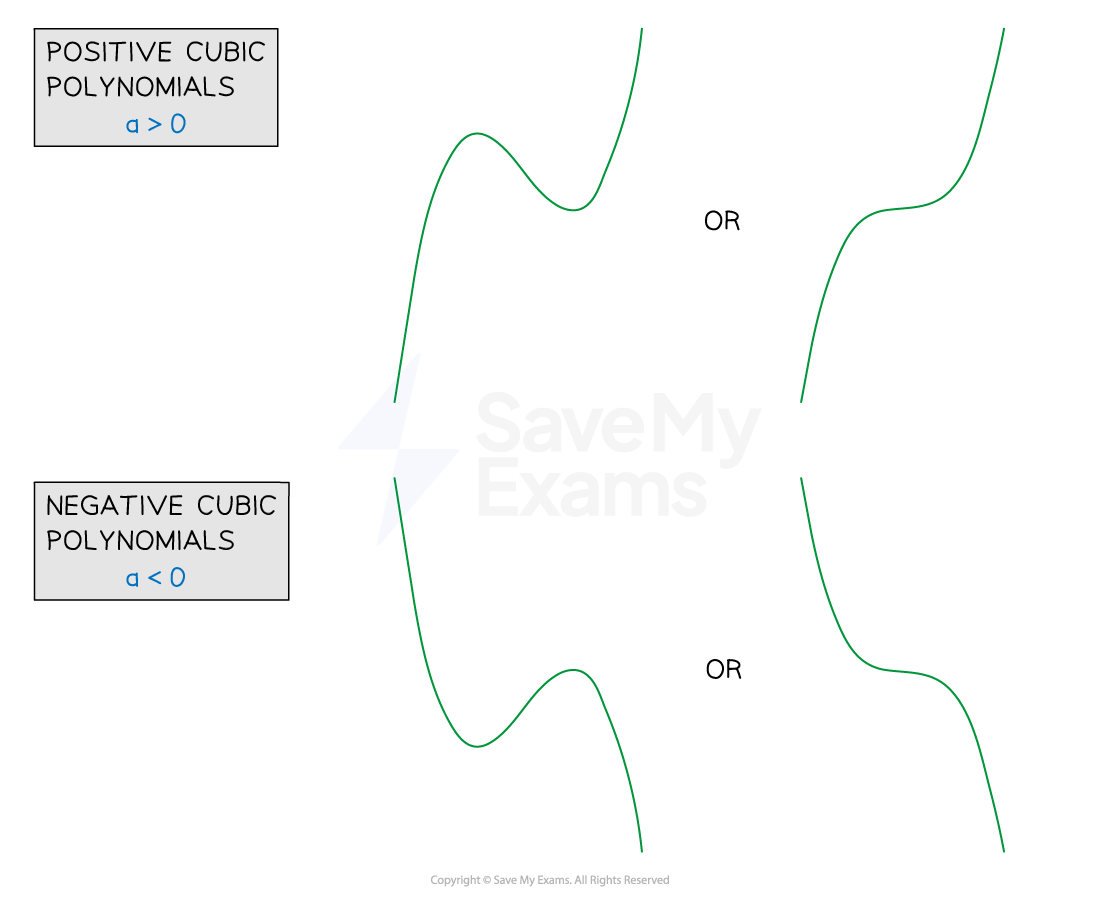
In general the graph of a cubic will take one of the four forms
- All are smooth curves

General shape of positive and negative cubic graphs

The exact form of a particular cubic will depend on:
- The number (and value) of roots ( $x$ -axis intercepts)
- The $y$ -axis intercept
- The sign of the coefficient of the $x^{3}$ term ( $a$ )
  - If $a > 0$ the graph is a positive cubic ('starts' in the bottom left, 'ends' in the top right)
  - If $a < 0$ the graph is a negative cubic ('starts' in the top left, 'ends' in the bottom right)
- The turning points

Key features of a polynomial graph - shape, intercept, turning points

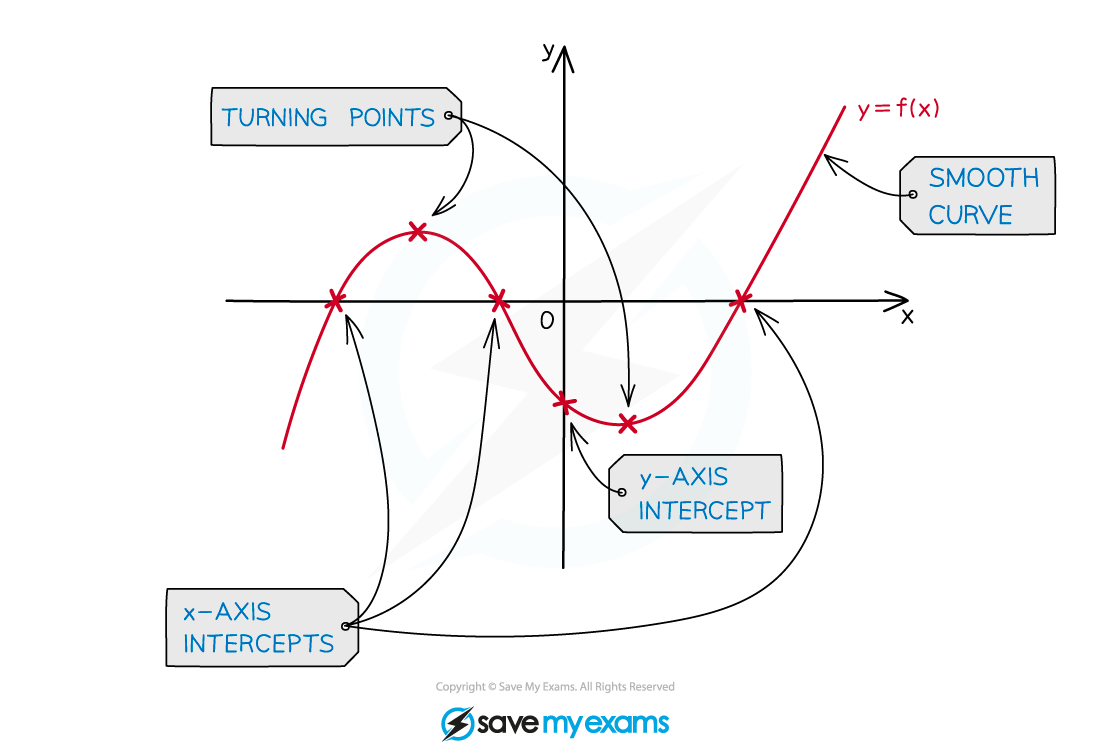
Cubics can have two turning points
- a maximum point and a minimum point
However, note that the graphs of $y = x^{3}$ and $y = - x^{3}$ :
- Do not have a maximum or minimum (turning points)
- Only cross the $x$ -axis once, at $x = 0$

How do I sketch the graph of a cubic?

STEP 1
Find the $y$ -axis intercept by setting $x = 0$
STEP 2
Find the $x$ -axis intercepts (roots) by setting $y = 0$
- In factorised form, this can be done by inspection
  - A cubic of the form $y = (x - p) (x - q) (x - r)$ has roots at $p, q$ and $r$
  - E.g. $y = (x - 2) (x - 3) (x + 5)$ has roots at 2, 3, and -5
- Any repeated roots will mean the graph touches the $x$ -axis
  - The graph does not cross the $x$ -axis
  - E.g. ${(x - 2)}^{2} (x + 1)$ touches the $x$ -axis at $x = 2$ , and intersects the $x$ -axis at $x = - 1$
STEP 3
Consider the shape of the graph
- Is it a positive cubic or a negative cubic?
- Where does the graph 'start' and 'end'?
STEP 4
Consider where any turning points should go
STEP 5
Sketch the graph with a smooth curve
Label points where the graph intercepts the $x$ and $y$ axes

Worked Example

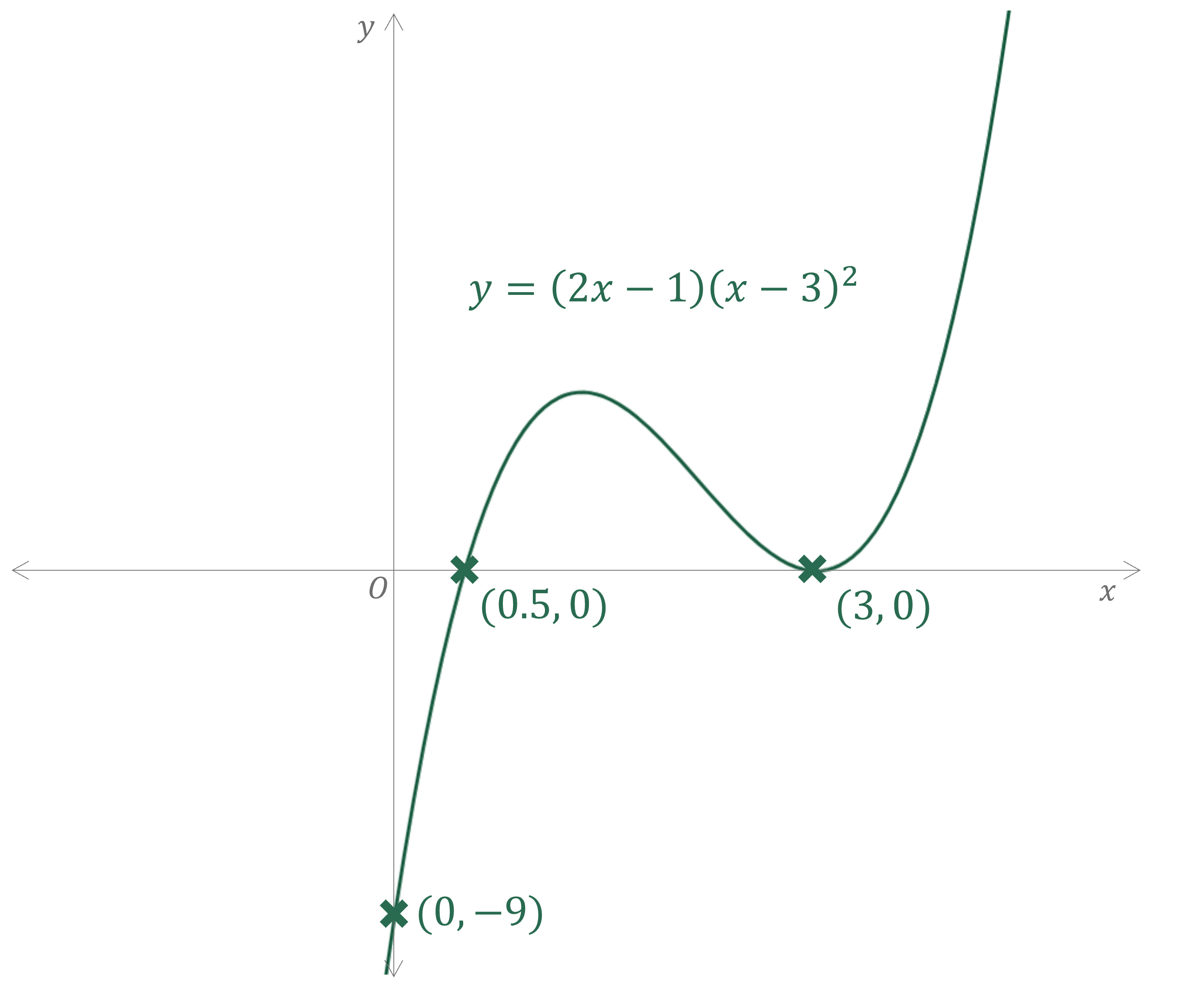
Sketch the graph of $y = (2 x - 1) {(x - 3)}^{2}$ .

STEP 1
Find the $y$ -axis intercept by substituting in $x = 0$

$y = (- 1) {(- 3)}^{2} = - 9$

STEP 2
Find the $x$ -axis intercepts by solving $y = 0$
Either bracket can be equal to zero

$\begin{array}{rcl} (2 x - 1) & = & 0 \\ x & = & \frac{1}{2} \end{array}$

$\begin{array}{rcl} {(x - 3)}^{2} & = & 0 \\ x & = & 3 \end{array}$
(repeated solution, as there are two $(x - 3)$ brackets

STEP 3
Consider the shape, and the 'start' and 'end' points:

$a > 0 (a = 2)$ so it is a positive cubic
$x = 3$ is a repeated root so the graph will touch the $x$ -axis at this point

STEP 4
Consider the turning points

One turning point (minimum) will need to be where the curve touches the $x$ -axis
The other (maximum) will need to be between the two roots $x = \frac{1}{2}$ and $x = 3$

STEP 5
Sketch a smooth curve with labelled intercepts

Worked example - final answer sketch of cubic showing intersections

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Next topic

Did this page help you?