AP®MathsCollege BoardCalculus BCStudy GuidesUnit 8: Applications of IntegrationAreas & Arc LengthsArea Between a Curve & x-Axis

Area Between a Curve & x-Axis (College Board AP® Calculus BC) : Study Guide

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on

College Board Calculus BCCollege Board Calculus AB

Area between a curve & x-axis

How do I find an area between a curve and the x-axis?

  • The value found when calculating the definite integral of a function y equals f open parentheses x close parentheses with respect to x between x equals a and x equals b, integral subscript a superscript b f open parentheses x close parentheses space italic d x

    • as long as f open parentheses x close parentheses greater or equal than 0 on the interval open square brackets a comma space b close square brackets

    • is equal to the area between the curve and the x-axis between x equals a and x equals b

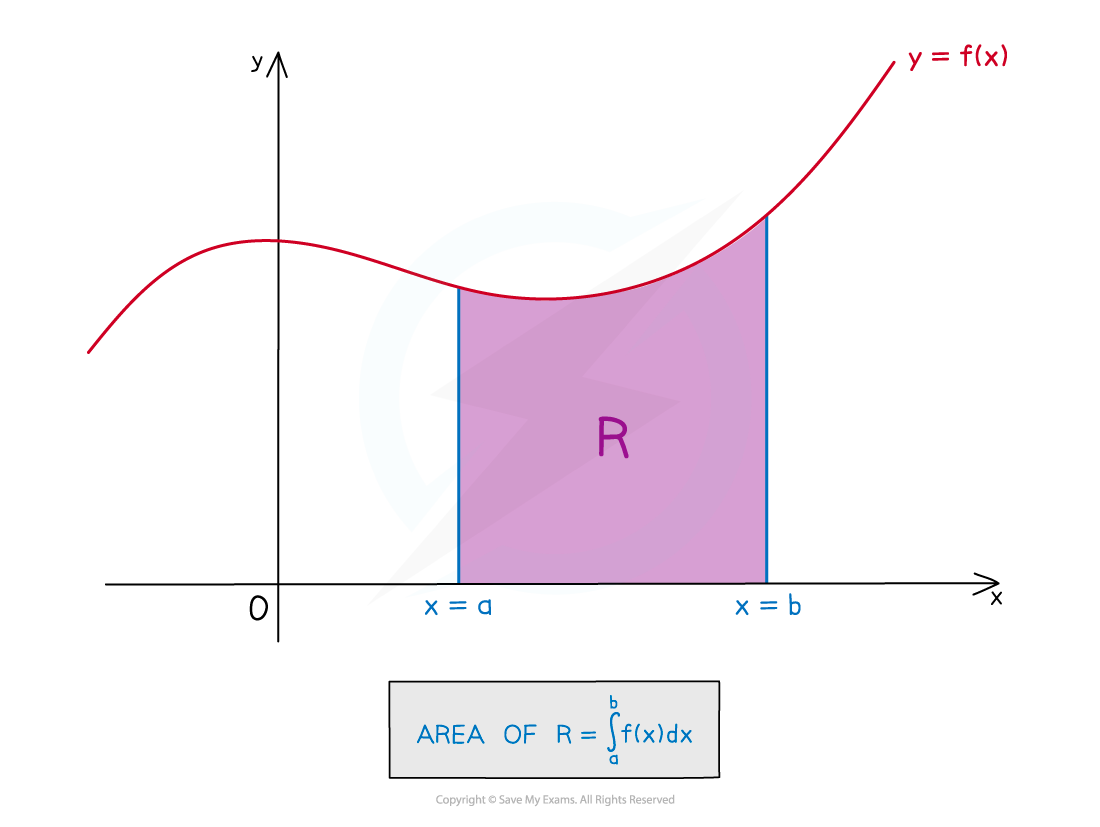
Graph of y = f(x) showing the area under the curve between x = a and x = b, shaded in purple and labeled R; integrals are used to find the area.

  • Consider finding the area between the graph of y equals 5 plus 2 x minus x squared and the x-axis, between x equals 1 and x equals 3

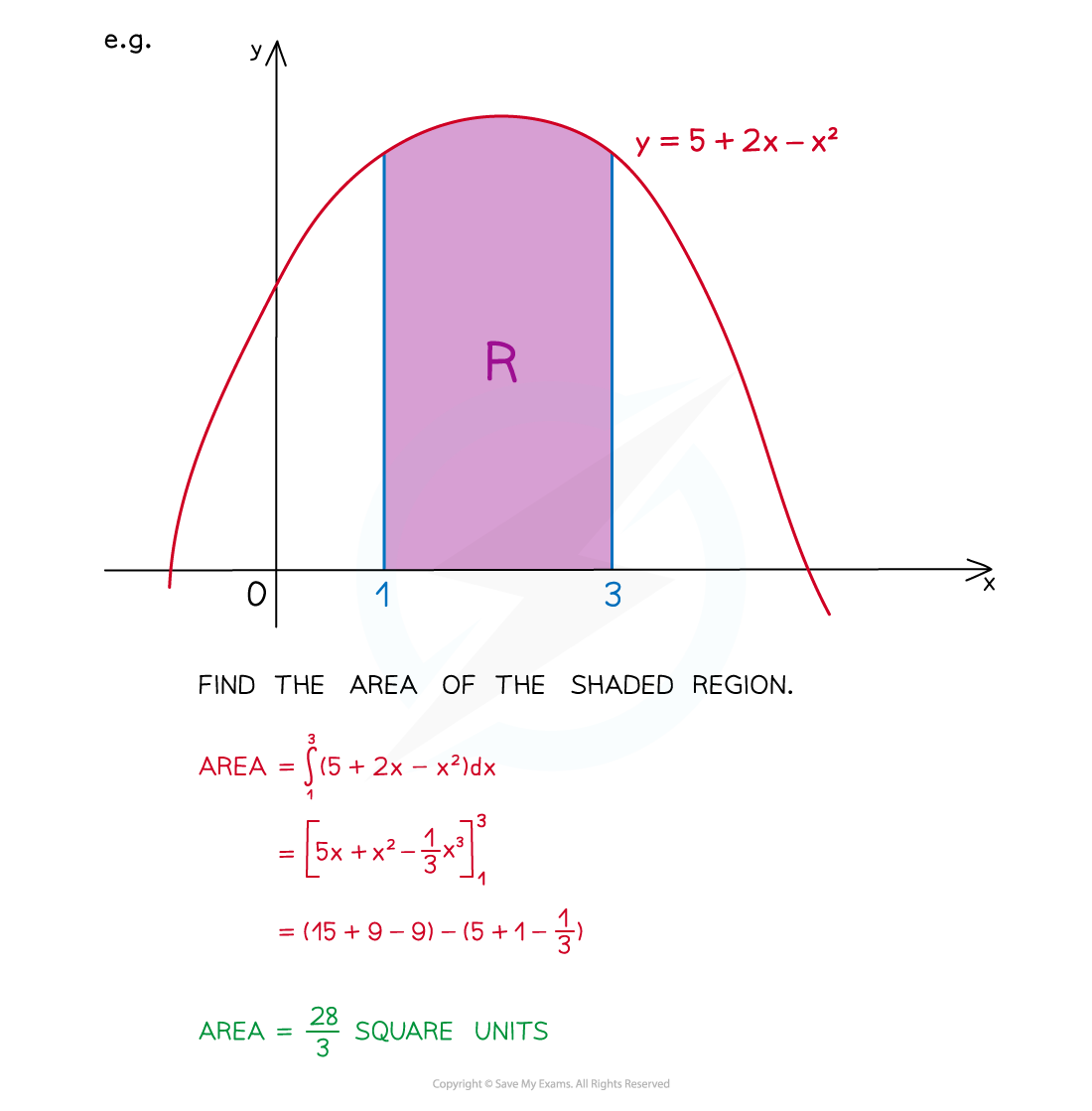
Graph of the function y = 5 + 2x - x^2 with a shaded region between x = 1 and x = 3, area calculated as 28/3 square units using integration.

  • This method of finding areas uses the idea of a definite integral as calculating an accumulation of change

    • f open parentheses x close parentheses times increment x is the area of a rectangle with height f open parentheses x close parentheses and width increment x

    • f open parentheses x close parentheses space d x is the limit of this area element as increment x rightwards arrow 0

    • The integral integral subscript a superscript b f open parentheses x close parentheses space d x sums up all these infinitesimal area elements between x equals a and x equals b

What if I am not told the limits?

  •  If limits are not provided they will often be the x-axis intercepts

    • Set y equals 0 and solve the equation to find the x-axis intercepts first

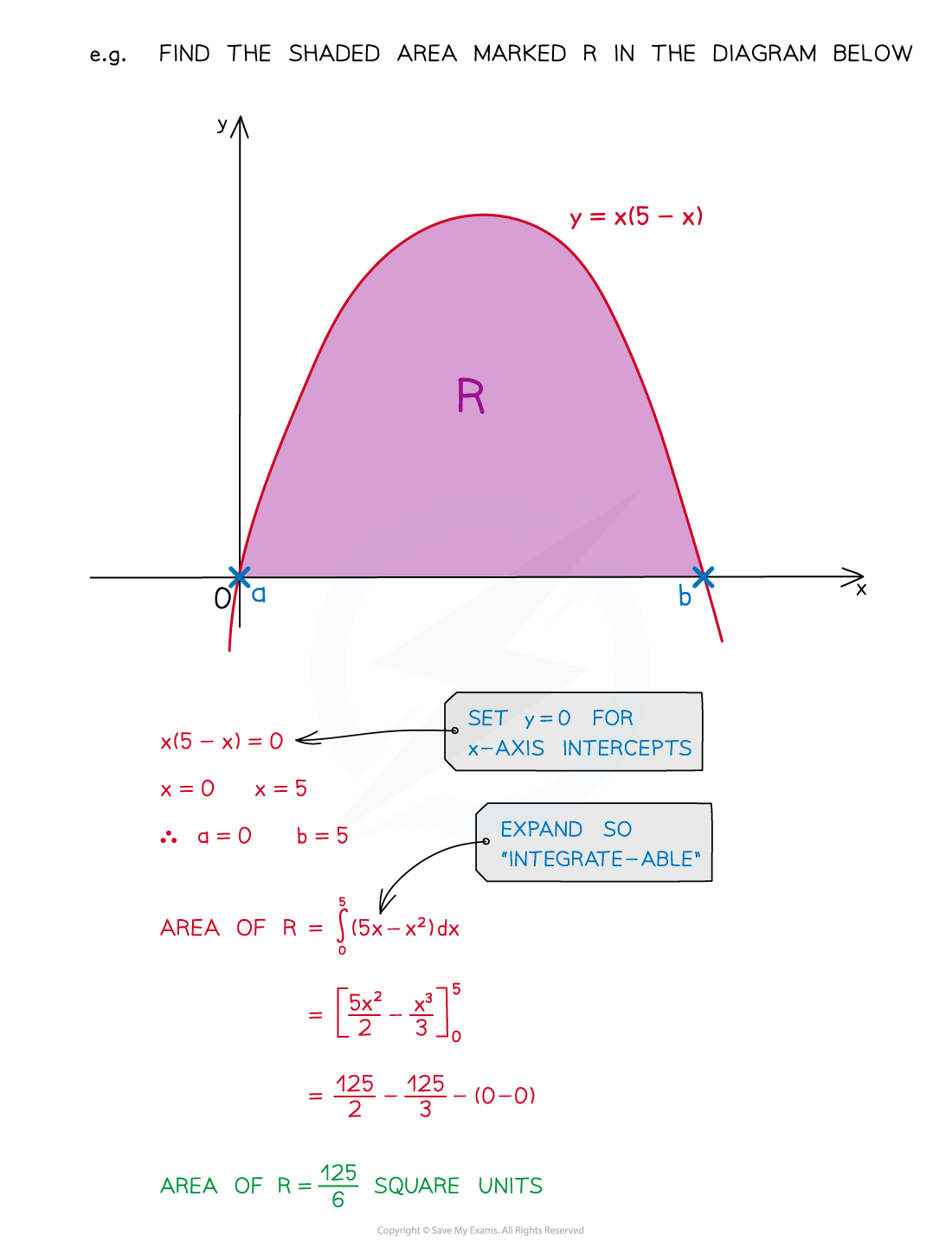
Graph showing the shaded area R under the curve y = x(5 - x). Finding the x-intercepts first, which are 0 and 5. Calculation shows area of R = 125/6 square units.

  • Remember that the y-axis (i.e. x equals 0) may also be one of the limits

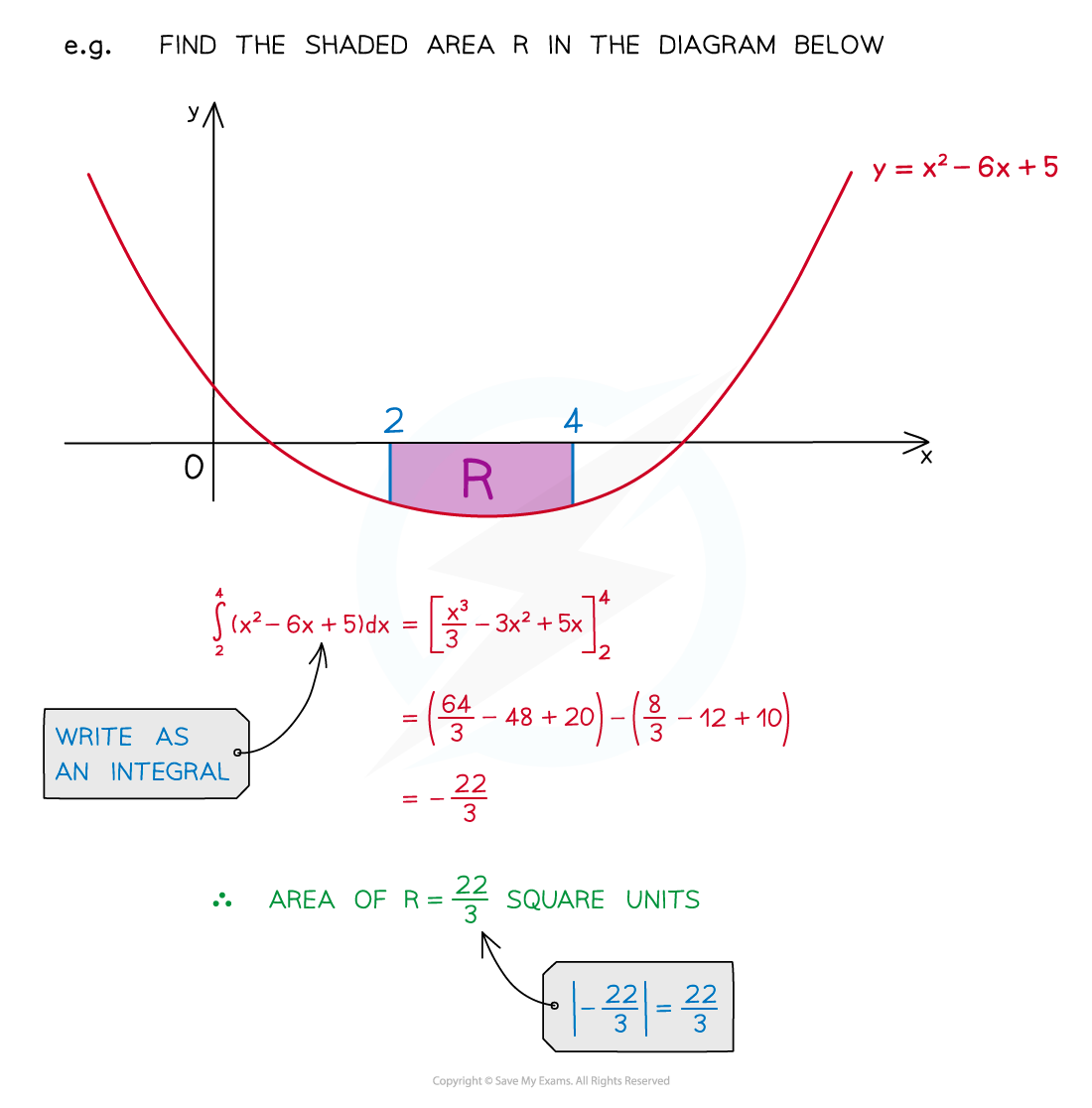
When is the area integral negative?

  •  If the area lies underneath the x-axis the value of the definite integral will be negative

    • However, an area cannot be negative

    • The area is equal to the modulus (absolute value) of the definite integral

  • If the area has some parts which are above the x-axis, and some which are below the x-axis

    • then see the method outlined in the 'Multiple Areas' study guide

Examiner Tips and Tricks

Always check whether you need to find the value of an integral, or an area.

  • When areas below the x-axis are involved, these will be two different values.

Graph of y = x^2 - 6x + 5 with shaded region R between x = 2 and x = 4. Integral calculation shows integral is -22/3, so the area is +22/3

You've read 1 of your 5 free study guides this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourself

Did this page help you?

Previous:Distance & SpeedNext:Area Between a Curve & y-Axis
Author
Reviewer
Jamie Wood

Author: Jamie Wood

Expertise: Maths Content Creator

Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Area Between a Curve & x-Axis