Acceleration (DP IB Physics) : Revision Note

Acceleration

• Acceleration is defined as:

  The rate of change of velocity

• Acceleration is a vector quantity and is measured in metres per second squared (m s^–2)

  • It describes how much an object's velocity changes every second

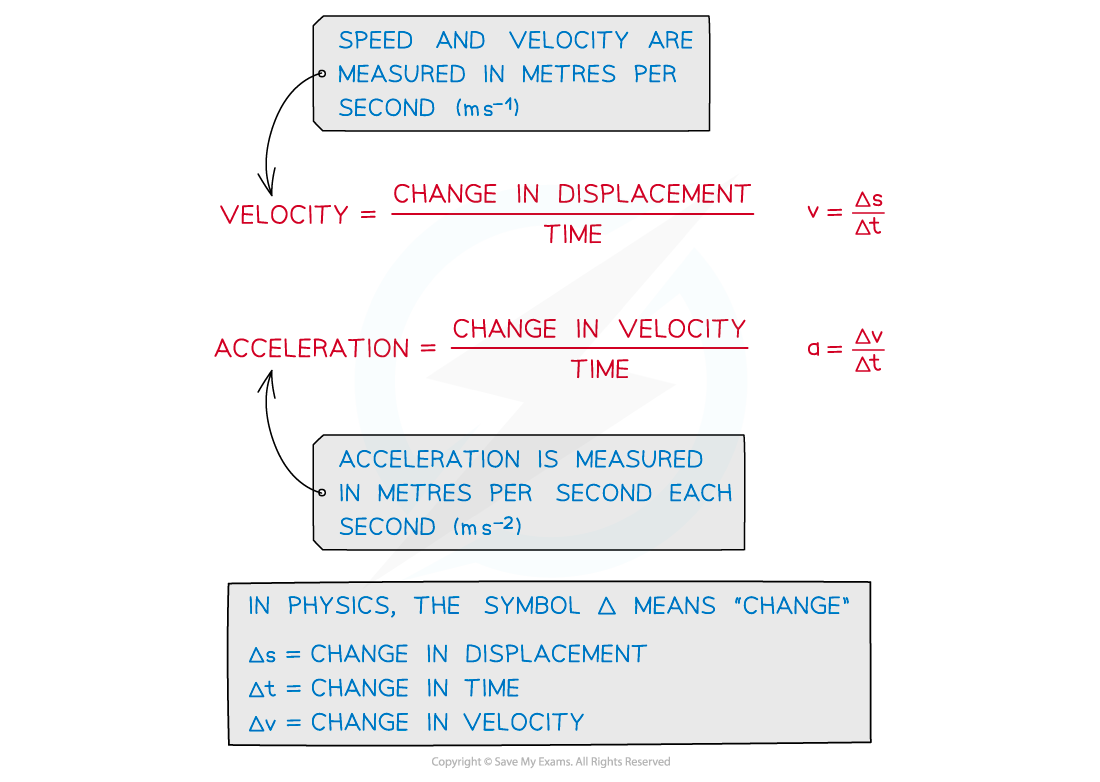
• The average acceleration of an object can be calculated using:

• Where:

  •  = average acceleration (m s^–2)

  •  = change in velocity (m s^–1)

  •  = total time taken (s)

• The change in velocity is the difference between the initial and final velocity, as written below:

change in velocity = final velocity − initial velocity

Equations linking displacement, velocity, and acceleration

Instantaneous Acceleration

• The instantaneous acceleration is the acceleration of an object at any given point in time

• This could be for an object with a constantly changing acceleration

  • An object accelerating is shown by a curved line on a velocity-time graph

What is a negative acceleration called?

• The acceleration of an object can be positive or negative, depending on whether the object is speeding up or slowing down

  • If an object is speeding up, its acceleration is positive

  • If an object is slowing down, its acceleration is negative (deceleration)

• However, acceleration can also be negative if it is accelerating in the negative direction

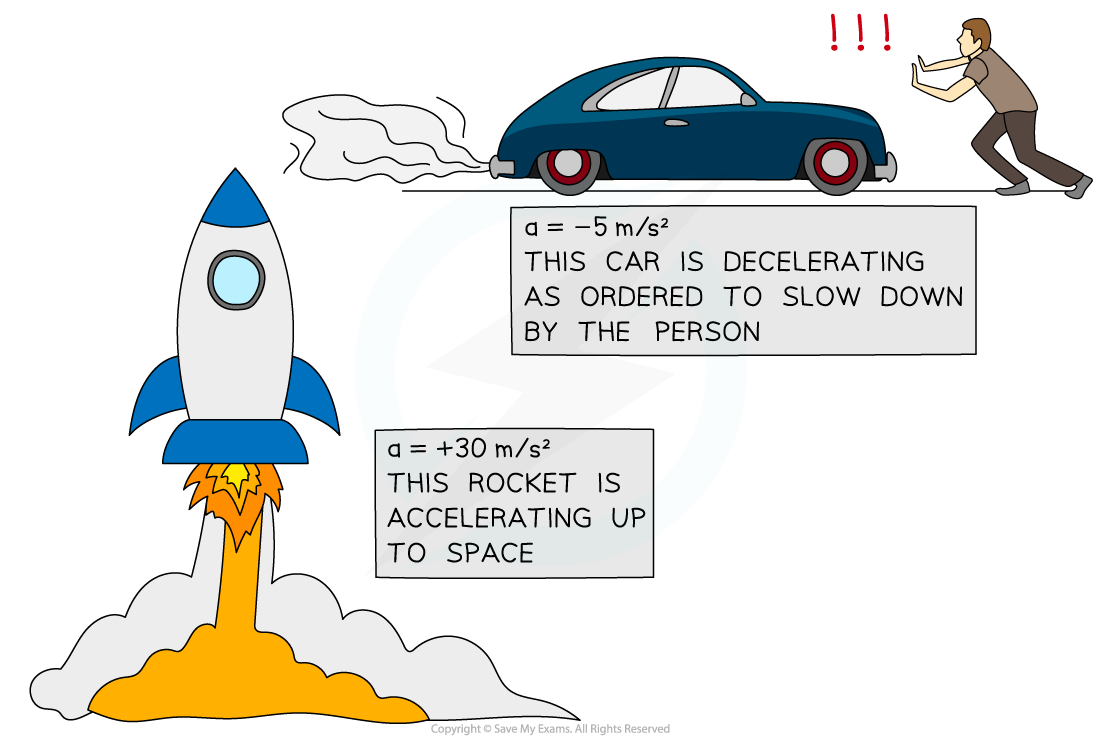
A rocket speeding up (accelerating) and a car slowing down (decelerating)