Roots of Complex Numbers

How do I find the square root of a complex number?

The square roots of a complex number will themselves be complex:
- i.e. if $z^{2} = a + b i$ then $z = c + d i$
We can then square ( $c + d i$ ) and equate it to the original complex number ( $a + b i$ ), as they both describe $z^{2}$ :
- $a + b i = {(c + d i)}^{2}$
Then expand and simplify:
- $a + b i = c^{2} + 2 c d i + d^{2} i^{2}$
- $a + b i = c^{2} + 2 c d i - d^{2}$
As both sides are equal we are able to equate real and imaginary parts:
- Equating the real components: $a = c^{2} - d^{2}$ (1)
- Equating the imaginary components: $b = 2 c d$ (2)
These equations can then be solved simultaneously to find the real and imaginary components of the square root
- In general, we can rearrange (2) to make $\frac{b}{2 d} = c$ and then substitute into (1)
- This will lead to a quartic equation in terms of d; which can be solved by making a substitution to turn it into a quadratic
The values of $d$ can then be used to find the corresponding values of $c$ , so we now have both components of both square roots ( $c + d i$ )
Note that one root will be the negative of the other root
- g. $c + d i$ and $- c - d i$

How do I use de Moivre’s Theorem to find roots of a complex number?

De Moivre’s Theorem states that a complex number in modulus-argument form can be raised to the power of n by

Raising the modulus to the power of n and multiplying the argument by n

When in modulus-argument (polar) form de Moivre’s Theorem can then be used to find the roots of a complex number by

Taking the nth root of the modulus and dividing the argument by n
If $z = r (\cos θ + isin θ)$ then $\sqrt[n]{z} = {[r (\cos (θ + 2 π k) + isin (θ + 2 π k))]}^{\frac{1}{n}}$

$k = 0, 1, 2, \dots, n - 1$
Recall that adding 2π to the argument of a complex number does not change the complex number
Therefore we must consider how different arguments will give the same result

This can be rewritten as $\sqrt[n]{z} = r^{\frac{1}{n}} (\cos (\frac{θ + 2 π k}{n}) + isin (\frac{θ + 2 π k}{n}))$

This can be written in exponential (Euler’s) form as

For $z^{n} = r e^{i θ}$ , $z = \sqrt[n]{r} e^{\frac{θ + 2 π k}{n} i}$

The nth root of complex number will have n roots with the properties:

The modulus is $\sqrt[n]{r}$ for all roots
There will be n different arguments spaced at equal intervals on the unit circle
This creates some geometrically beautiful results:

The five roots of a complex number raised to the power 5 will create a regular pentagon on an Argand diagram
The eight roots of a complex number raised to the power 8 will create a regular octagon on an Argand diagram
The n roots of a complex number raised to the power n will create a regular n-sided polygon on an Argand diagram

Sometimes you may need to use your GDC to find the roots of a complex number

Using your GDC’s store function will help when entering complicated modulus and arguments
Make sure you choose the correct form to enter your complex number in
Your GDC should be able to give you the answer in your preferred form

Examiner Tip

De Moivre's theorem makes finding roots of complex numbers very easy, but you must be confident converting from Cartesian form into Polar and Euler's form first
- If you are in a calculator exam your GDC will be able to do this for you but you must clearly show how you got to your answer
- You must also be prepared to do this by hand in a non-calculator paper

Worked example

Find the square roots of 5 + 12i, giving your answers in the form a + bi.

k-4_ksf4_1-9-3-ib-aa-hl-de-moivres-theorem-we-solution-2

Solve the equation

z^{3} = - 4 + 4 \sqrt{3} i

giving your answers in the form r cis θ.

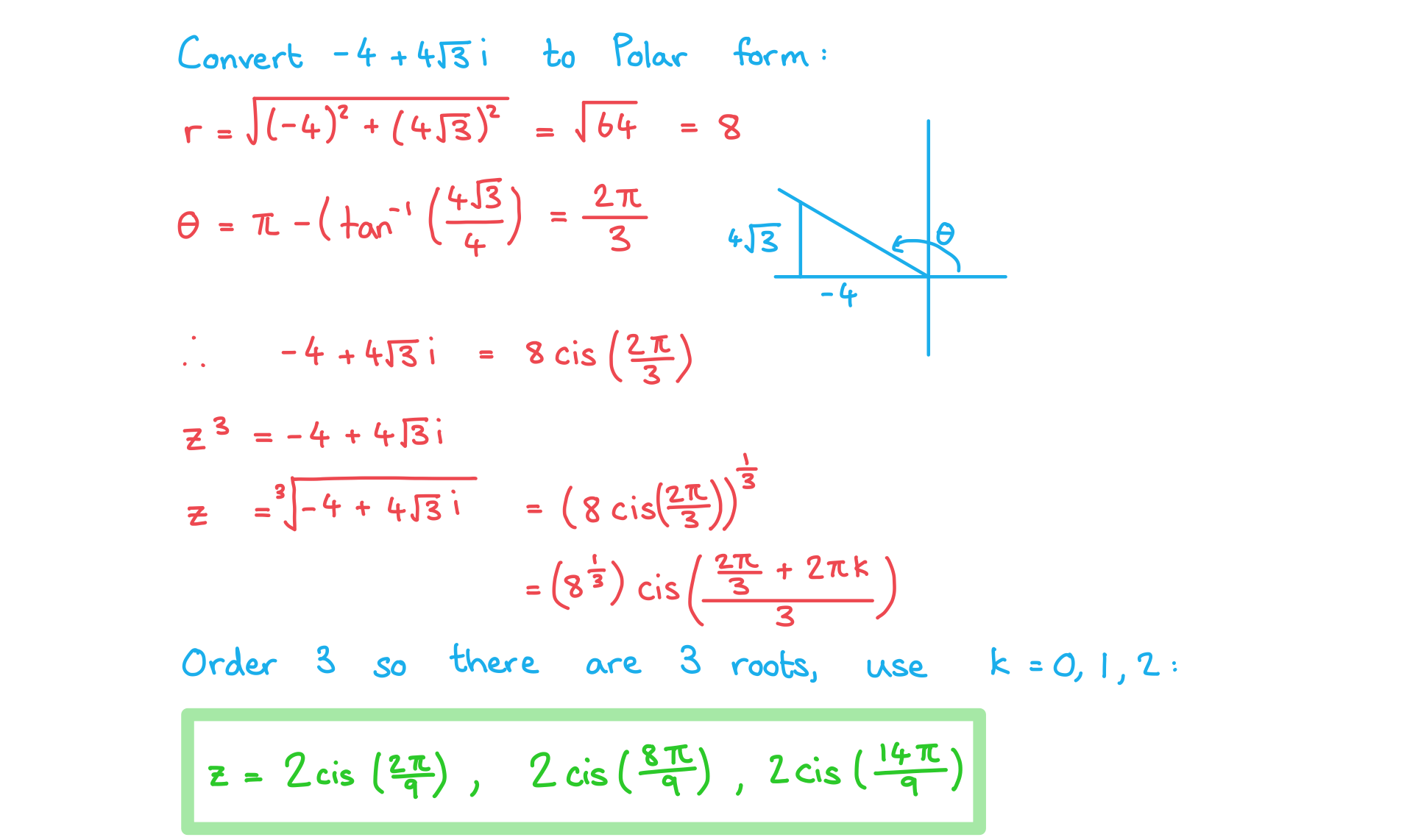
1-9-3-ib-aa-hl-roots-of-cn-we-solution

Roots of Complex Numbers (DP IB Maths: AA HL)

Revision Note

How do I find the square root of a complex number?

How do I use de Moivre’s Theorem to find roots of a complex number?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Number & Algebra

1.1 Number & Algebra Toolkit

1.1.1 Standard Form

1.1.2 Laws of Indices

1.1.3 Partial Fractions

1.2 Exponentials & Logs

1.2.1 Introduction to Logarithms

1.2.2 Laws of Logarithms

1.2.3 Solving Exponential Equations

1.3 Sequences & Series

1.3.1 Language of Sequences & Series

1.3.2 Arithmetic Sequences & Series

1.3.3 Geometric Sequences & Series

1.3.4 Applications of Sequences & Series

1.3.5 Compound Interest & Depreciation

1.4 Simple Proof & Reasoning

1.4.1 Proof

1.5 Further Proof & Reasoning

1.5.1 Proof by Induction

1.5.2 Proof by Contradiction

1.6 Binomial Theorem

1.6.1 Binomial Theorem

1.6.2 Extension of The Binomial Theorem

1.7 Permutations & Combinations

1.7.1 Counting Principles

1.7.2 Permutations & Combinations

1.8 Complex Numbers

1.8.1 Intro to Complex Numbers

1.8.2 Modulus & Argument

1.8.3 Introduction to Argand Diagrams

1.9 Further Complex Numbers

1.9.1 Geometry of Complex Numbers

1.9.2 Forms of Complex Numbers

1.9.3 Complex Roots of Polynomials

1.9.4 De Moivre's Theorem

1.9.5 Roots of Complex Numbers

1.10 Systems of Linear Equations

1.10.1 Systems of Linear Equations

1.10.2 Algebraic Solutions

2. Functions

2.1 Linear Functions & Graphs

2.1.1 Equations of a Straight Line

2.2 Quadratic Functions & Graphs

2.2.1 Quadratic Functions

2.2.2 Factorising & Completing the Square

2.2.3 Solving Quadratics

2.2.4 Quadratic Inequalities

2.2.5 Discriminants

2.3 Functions Toolkit

2.3.1 Language of Functions

2.3.2 Composite & Inverse Functions

2.3.3 Symmetry of Functions

2.3.4 Graphing Functions

2.4 Other Functions & Graphs

2.4.1 Exponential & Logarithmic Functions

2.4.2 Solving Equations

2.4.3 Modelling with Functions

2.5 Reciprocal & Rational Functions

2.5.1 Reciprocal & Rational Functions

2.6 Transformations of Graphs

2.6.1 Translations of Graphs

2.6.2 Reflections of Graphs

2.6.3 Stretches Graphs

2.6.4 Composite Transformations of Graphs

2.7 Polynomial Functions

2.7.1 Factor & Remainder Theorem

2.7.2 Polynomial Division

2.7.3 Polynomial Functions

2.7.4 Roots of Polynomials

2.8 Inequalities

2.8.1 Solving Inequalities Graphically

2.8.2 Polynomial Inequalities

2.9 Further Functions & Graphs