Revision NotesExam QuestionsFlashcardsPast Papers
IGCSEBusinessCambridge (CIE)Revision Notes4. Operations Management4.4 Costs, Scale of Production & Break-even AnalysisBreak-Even Analysis

Syllabus Edition

First teaching 2025

First exams 2027

Break-Even Analysis (Cambridge (CIE) IGCSE Business): Revision Note

Exam code: 0450, 0986 & 0264, 0774

Lisa Eades

Written by: Lisa Eades

Reviewed by: Steve Vorster

Updated on

The concept of break-even

  • The break-even point is the number of units that need to be sold for total costs to equal the sales revenue

    • It helps businesses understand the minimum level of sales or output they need to achieve in order to cover all costs

    • This helps business managers to make informed decisions about pricing and production volumes

Elements of a break-even analysis

Three interlocking hexagons labelled "Fixed Costs", "Variable Costs", and "Revenue" in blue, beige, and pink respectively.
Variable costs, fixed costs and sales revenue are all used in calculating the break-even point

  • Fixed costs do not change, regardless of the level of production or sales

    • E.g. rent, salaries and insurance

  • Variable costs vary with the level of production or sales

    • E.g. raw materials, direct labour costs, packaging and shipping costs

  • Sales revenue is money gained from selling products, calculated using the formula

Sales space revenue space equals space Number space of space items space sold space cross times space Selling space price

The break-even chart

  • Break-even charts show the number of units a business must sell in order to break-even

  • In order to construct a break-even chart, the business needs to know the estimated fixed costs, variable costs and sales revenue

Worked Example

Steps to construct a break-even chart

Step 1: Identify fixed costs, variable costs and sales revenue at different levels of output

  • Tee Crazy Ltd has the following cost and revenue data:

    •  Fixed costs are $8,800 per year

    • The variable costs of each t-shirt is $4

    • Each t-shirt is sold for a price of $10

    • Its factory can produce a maximum output of 3000 t-shirts per year 

Costs and revenue summary for Tee-Crazy Ltd.

 

0 units

500 units

3000 units

Fixed Costs

8,800

8,800

8,800

Variable Costs

0

2,000

12,000

Total Costs

8,800

10,800

20,800

Total Revenue

0

5,000

30,000

Step 2: Draw the axes and plot the fixed costs line

  • The x-axis should extend to the maximum output level

    • In this case it extends to 3,000 units

  • The y-axis should extend to the highest value in the table

    • In this case the highest value is $30,000

Two graphs illustrating the steps to create a cost-output chart; step 1 shows axes, step 2 adds a horizontal fixed cost line at $8,800 across outputs.

  • The fixed cost line is a horizontal line at $8,800, as fixed costs remain constant at all levels of output

Step 3: Plot the total costs line

Graph showing monthly revenue and costs versus output level in units. Fixed costs are $8,800; total costs are $20,800 at 3,000 units. Instructions detail cost calculations.

  • The total cost line slopes upwards, starting at $8,800 at 0 units of output, rising to $20,800 at 3,000 units of output

Step 4: Plot the revenue line

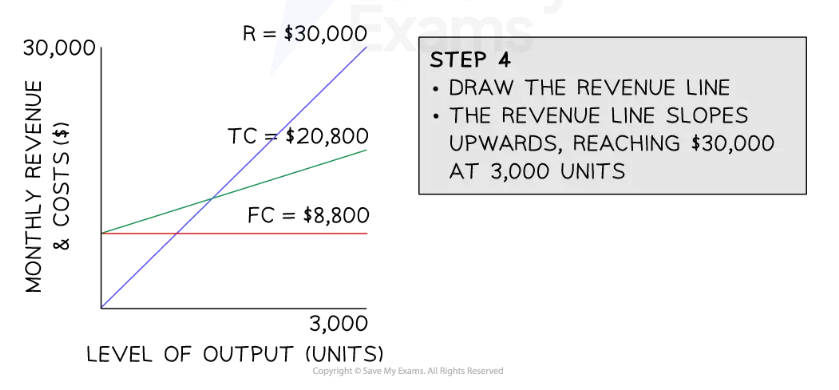
Graph showing revenue and costs against output. Revenue line rises to $30,000 at 3,000 units. Annotation explains drawing the revenue line.

  • The revenue line slopes upwards, starting at $0 at 0 units of output, rising to $30,000 at 3,000 units of output

Step 5: Identify the break-even point

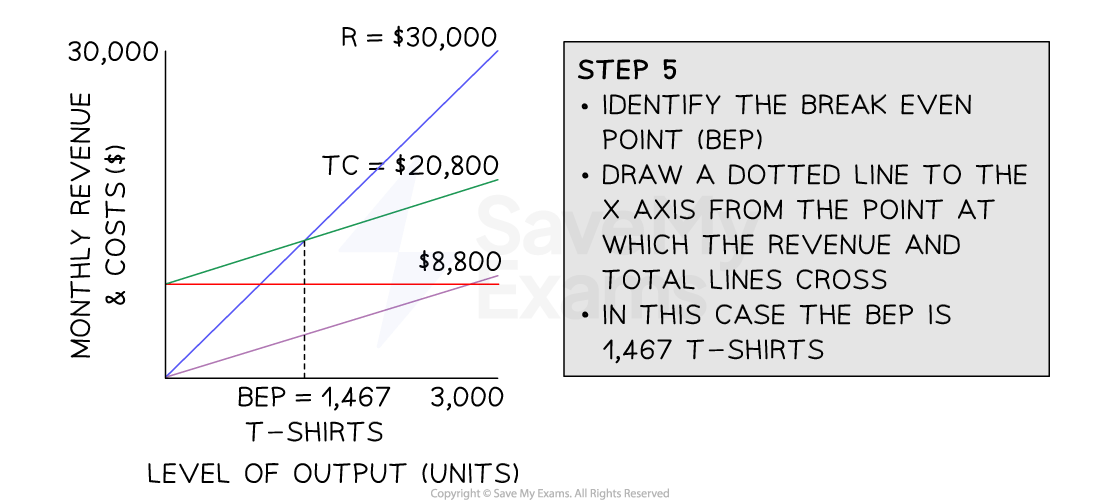
Graph showing break-even point analysis for T-shirts at 1,467 units, with revenue at $30,000, total cost at $20,800, and a panel with explanation.

  • The break-even point is where the revenue line crosses the total costs line

    • Read the break-even output on the x-axis

    • In this case, the break-even point is 1,467 units

Examiner Tips and Tricks

When drawing break-even charts, label all key elements clearly – fixed costs, total costs, total revenue, and break-even point – as missing labels often loses easy marks

Calculating break-even output

  • The break-even point can be calculated using the formula

space Breakeven space point space equals space fraction numerator Fixed space costs over denominator open parentheses Selling space price space minus space Variable space cost space per space unit close parentheses end fraction

Worked Example

Mięsisty Burgers has the following financial information for the month of May

 

€ May

Raw materials for each burger

2.10

Packaging for each burger

0.20

Fixed costs

1730

Selling price of each burger

4.95

Using the information in the table, calculate the level of output required to break even in May. You are advised to show your workings.

(3)

Step 1: Calculate the variable costs per burger

Variable space cost space per space burger space equals space Raw space materials space plus space Packaging equals space € 2.10 space plus space € 0.20 space equals space € 2.30  (1)

Step 2: Substitute the values into the break-even formula

  Break space even space point space in space units space equals space fraction numerator Fixed space Cost over denominator stretchy left parenthesis Selling space price space minus space Variable space cost stretchy right parenthesis end fraction equals space fraction numerator 1 comma 730 over denominator stretchy left parenthesis 4.95 space minus space 2.30 stretchy right parenthesis end fraction equals space fraction numerator 1 comma 730 over denominator stretchy left parenthesis 2.65 stretchy right parenthesis end fraction equals space 652.83      (1)

Step 3: Round to the nearest unit

  • 653 burgers need to be sold to break even in May  (1)

Examiner Tips and Tricks

Always round up the break-even point to the nearest whole unit

The margin of safety

  • The margin of safety is the amount by which the number of units sold is greater than the break-even point

    • The margin of safety provides useful information to a firm on how many sales they could lose before they start making a loss

  • The margin of safety can be calculated using the following formula:

Margin space of space safety space equals Quantity space of space sales space minus space Break minus even space level space of space sales 

  • Businesses want their margin of safety to be as large as possible

    • This means that if demand for their products drops unexpectedly, the business will continue to make a profit

Worked Example

The diagram shows the weekly break-even diagram for the Yorkshire Rare Breed Sausage Company. On average, the business sells 3,200 units each week.

Graph showing weekly output and costs for Yorkshire Rare Breed Sausage Company, with lines for fixed costs, total costs, and revenue.
Output, costs and revenues of the Yorkshire Rare Breed Sausage Company

Using the diagram, calculate the weekly margin of safety. Show your workings and the formula used.

(2)

Step 1: Identify the break-even output from the graph

 = 2,500 units (1)

Step 2: Subtract the break-even output from the actual output

   Margin space of space safety space equals Quantity space of space sales space minus space Break minus even space level space of space sales equals space 3 comma 200 space minus space 2 comma 500 equals space 700 space units (1)

Examiner Tips and Tricks

Use a ruler to help you to read break-even charts accurately.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Economies & Diseconomies of ScaleNext:Using Break-Even Analysis to Make Decisions
    Author
    Reviewer
    Lisa Eades

    Author: Lisa Eades

    Expertise: Business Content Creator

    Lisa has taught A Level, GCSE, BTEC and IBDP Business for over 20 years and is a senior Examiner for Edexcel. Lisa has been a successful Head of Department in Kent and has offered private Business tuition to students across the UK. Lisa loves to create imaginative and accessible resources which engage learners and build their passion for the subject.

    Steve Vorster

    Reviewer: Steve Vorster

    Expertise: Economics & Business Subject Lead

    Steve has taught A Level, GCSE, IGCSE Business and Economics - as well as IBDP Economics and Business Management. He is an IBDP Examiner and IGCSE textbook author. His students regularly achieve 90-100% in their final exams. Steve has been the Assistant Head of Sixth Form for a school in Devon, and Head of Economics at the world's largest International school in Singapore. He loves to create resources which speed up student learning and are easily accessible by all.