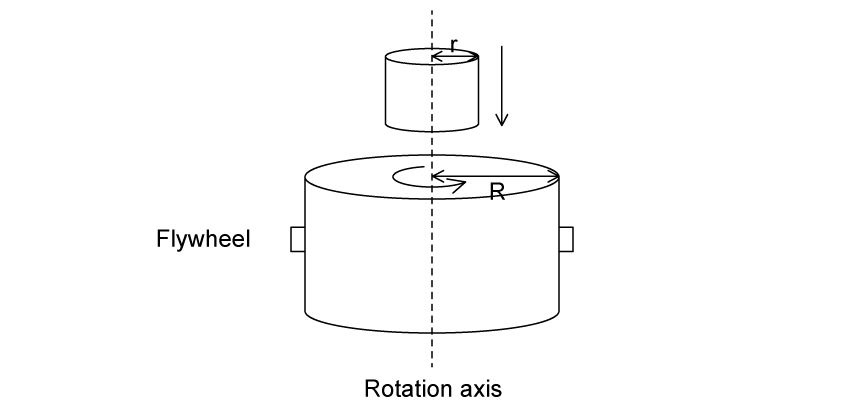
A disc rotates from rest with an angular acceleration of 5.0 rad s−2 for 3.0 seconds.
Calculate the final angular speed of the disc and state the correct unit.
Calculate the angular displacement of the disc after 3.0 s.
Calculate the number of complete revolutions that the disc has rotated through.
Was this exam question helpful?