The Ideal Gas Equation (OCR A Level Chemistry A): Revision Note

Ideal gas equation & calculations

Kinetic theory of gases

• The kinetic theory of gases explains the behaviour of gas molecules, which are in constant motion

• It is based on these assumptions:

  • Gas molecules move rapidly and randomly

  • The volume of individual gas molecules is negligible

  • There are no attractive or repulsive forces between molecules

  • Collisions between molecules are elastic

    • This means that no kinetic energy is lost

  • Temperature is proportional to the average kinetic energy of the molecules

• Gases that follow this model exactly are called ideal gases

• Real gases do not follow all these assumptions perfectly

  • But, they often behave similarly under standard conditions

Ideal gases

• The volume that an ideal gas occupies depends on:

  • Pressure

  • Temperature

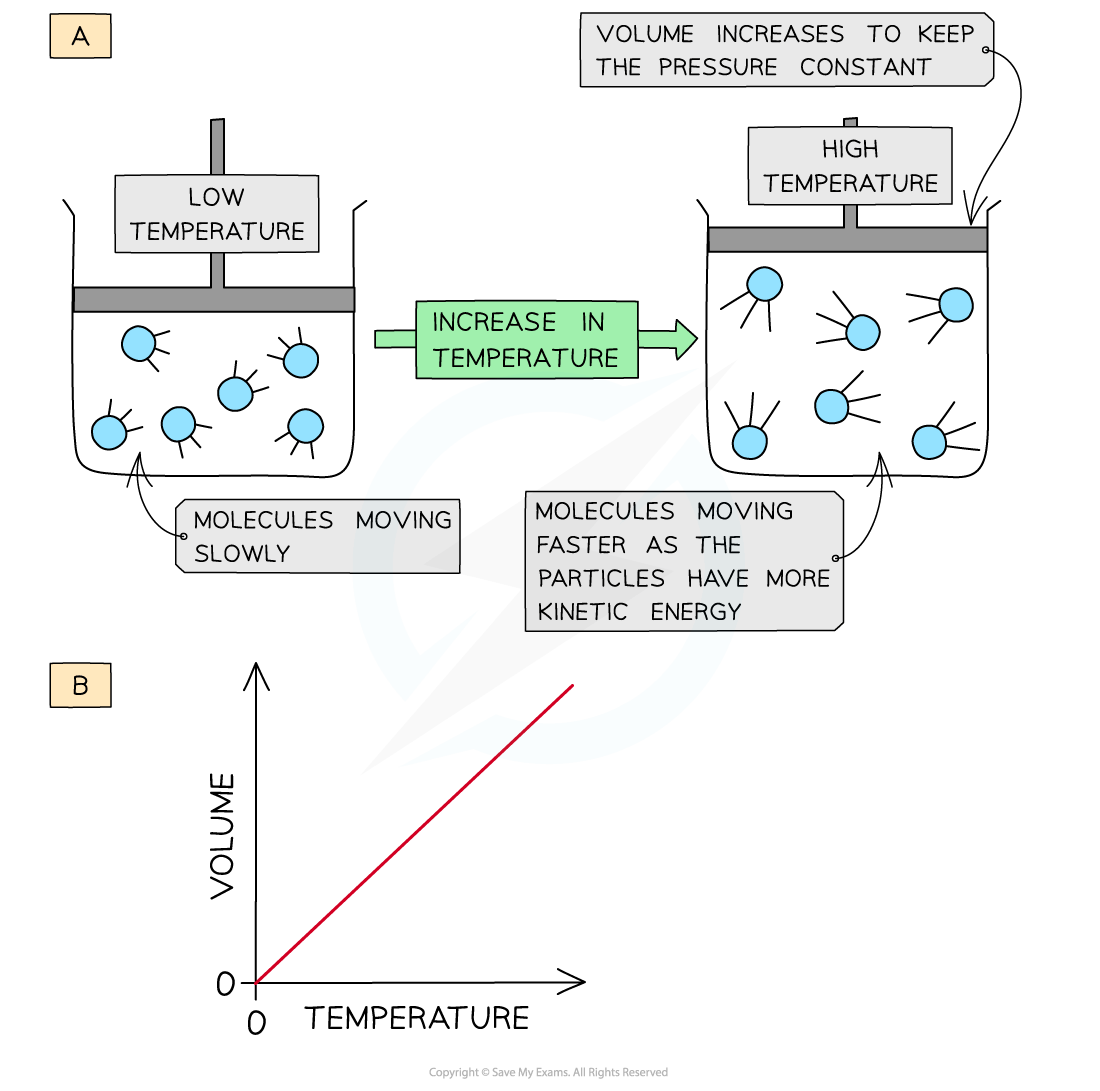
• When a gas is heated at constant pressure:

  • Particles gain kinetic energy

  • They collide more frequently with the container walls

  • To maintain constant pressure, the particles must spread out

    • So, the volume increases

• Therefore, volume is directly proportional to temperature at constant pressure

Limitations of the ideal gas law

• At low temperatures and high pressures, real gases deviate from ideal behaviour

  • Molecules are closer together

  • Intermolecular forces (e.g. London forces, permanent dipoles) become significant

  • These forces reduce collisions with container walls

    • Therefore, the measured pressure is lower than predicted

  • The actual volume of gas particles is no longer negligible

    • Therefore, the measured volume is lower than predicted

• Therefore, under these conditions:

  • The assumption of no attraction between particles is invalid

  • The assumption that particles have negligible volume is also invalid

Ideal gas equation

• The ideal gas equation shows the relationship between pressure, volume, temperature, and number of moles:

pV = nRT

• Where:

  • p = pressure (pascals, Pa)

  • V = volume (m³)

  • n = number of moles of gas (mol)

  • R = gas constant (8.314 J mol^-1 K^-1)

  • T = temperature (kelvin, K)