Completing the Square (AQA GCSE Maths): Revision Note

Completing the square

How can I rewrite the first two terms of a quadratic expression as the difference of two squares?

• Look at the quadratic expression x² + bx + c 

• The first two terms can be written as the difference of two squares using the following rule

is the same as where is half of 

• Check this is true by expanding the right-hand side

  • Is the same as ?
    

    • Yes: (x + 1)(x + 1) - 1² = x² + 2x + 1 - 1 = x² + 2x

• This works for negative values of b too

  •   can be written as  which is 

  • A negative b does not change the sign at the end

How do I complete the square?

• Completing the square is a way to rewrite a quadratic expression in a form containing a squared bracket

• To complete the square on x² + 10x + 9

  • Use the rule above to replace the first two terms, x² + 10x, with (x + 5)² - 5²

  • then add 9:  (x + 5)² - 5² + 9

  • simplify the numbers:  (x + 5)² - 25 + 9

  • answer: (x + 5)² - 16 

How do I complete the square when there is a coefficient in front of the x² term?

• You first need to take out as a factor of the x² and x terms only

  • Factorise the first two terms

  • 

    • Use square-shaped brackets here to avoid confusion with round brackets later

• Then complete the square on the bit inside the brackets:

  • This gives 

    • where p is half of 

• Finally multiply this expression through by a (from outside the square brackets) and add the c on to the end

  • 

    • This looks far more complicated than it is in practice!

  • Usually you are asked to give your final answer in the form   

  • For example, y = 4x² + 16x + 5

    • Factorise out 'a' on the right-hand side (use square brackets)

      • y = 4[x² + 4x] + 5

    • Replace x² + 4x with (x + 2)² - 2²  (because p = = 2)

      • y = 4[(x + 2)² - 2²] + 5

    • Simplify the terms inside the square brackets

      • y = 4[(x + 2)² - 4] + 5

    • Multiply everything inside the square brackets by 4

      • y = 4(x + 2)² - 16 + 5

    • Simplify to get the final answer

      • y = 4(x + 2)² - 11

• For quadratics like , do the above but with a = -1

How do I find the turning point by completing the square?

• Completing the square helps us find the turning point on a quadratic graph

  • If  then the turning point is at

    • Notice the negative sign in the x-coordinate

    • This links to transformations of graphs

    • A translation of by p to the left and q up

  • If  then the turning point is still at 

    • The a does not change the coordinates

    • The turning point is a minimum point if a > 0

    • or a maximum point if a < 0

• This can also help you create the equation of a quadratic when given the turning point

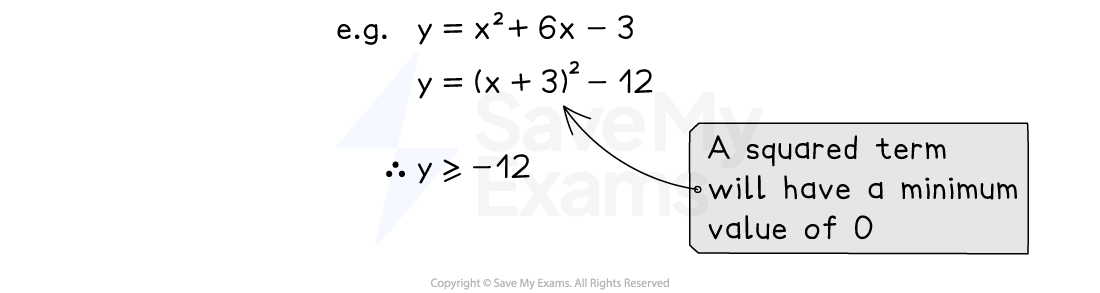
• It can also be used to prove or show results using the fact that any squared term, such as the squared bracket (x ± p)², will always be greater than or equal to 0

  • You cannot square a number and get a negative value

  • The smallest a squared term can be is 0