Cells & Surface Area (College Board AP® Biology): Study Guide

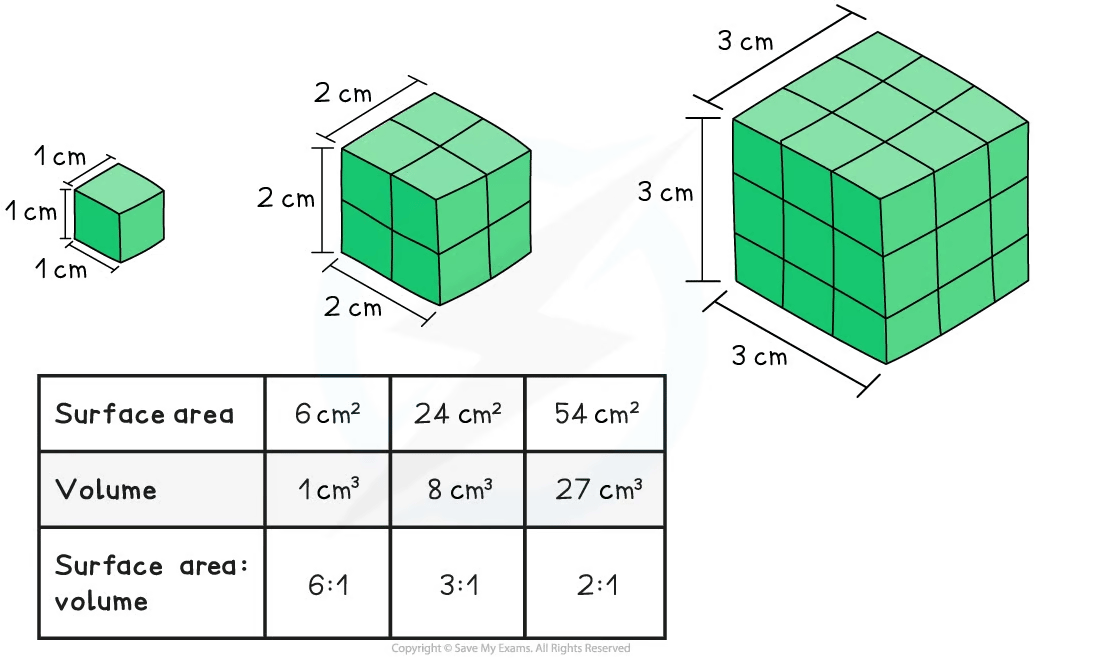
Surface area-to-volume ratio

• Surface area and volume are both very important factors in the exchange of materials in organisms

  • Surface area refers to the total area of the organism that is exposed to the external environment

  • Volume refers to the total internal volume of the organism, or the total amount of space inside the organism

• As the surface area and volume of an organism increase (as the size of an organism increases), the surface area : volume ratio decreases

  • This is because volume increases much more rapidly than surface area as size increases

Importance of surface area-to-volume ratios

• Having a high surface area-to-volume ratio increases the ability of a biological system to perform the following important functions:

  • obtain necessary resources, e.g. oxygen, glucose, amino acids

  • eliminate waste products, e.g. carbon dioxide, urea

  • acquire or dissipate thermal energy (heat)

  • exchange chemicals with the surroundings, e.g. secreting or binding to hormones at the cell surface

Calculating surface area-to-volume ratios

• The SA:V ratios of different biological shapes can be calculated using mathematical formulae

	Sphere	Cube	Rectangular solid	Cylinder
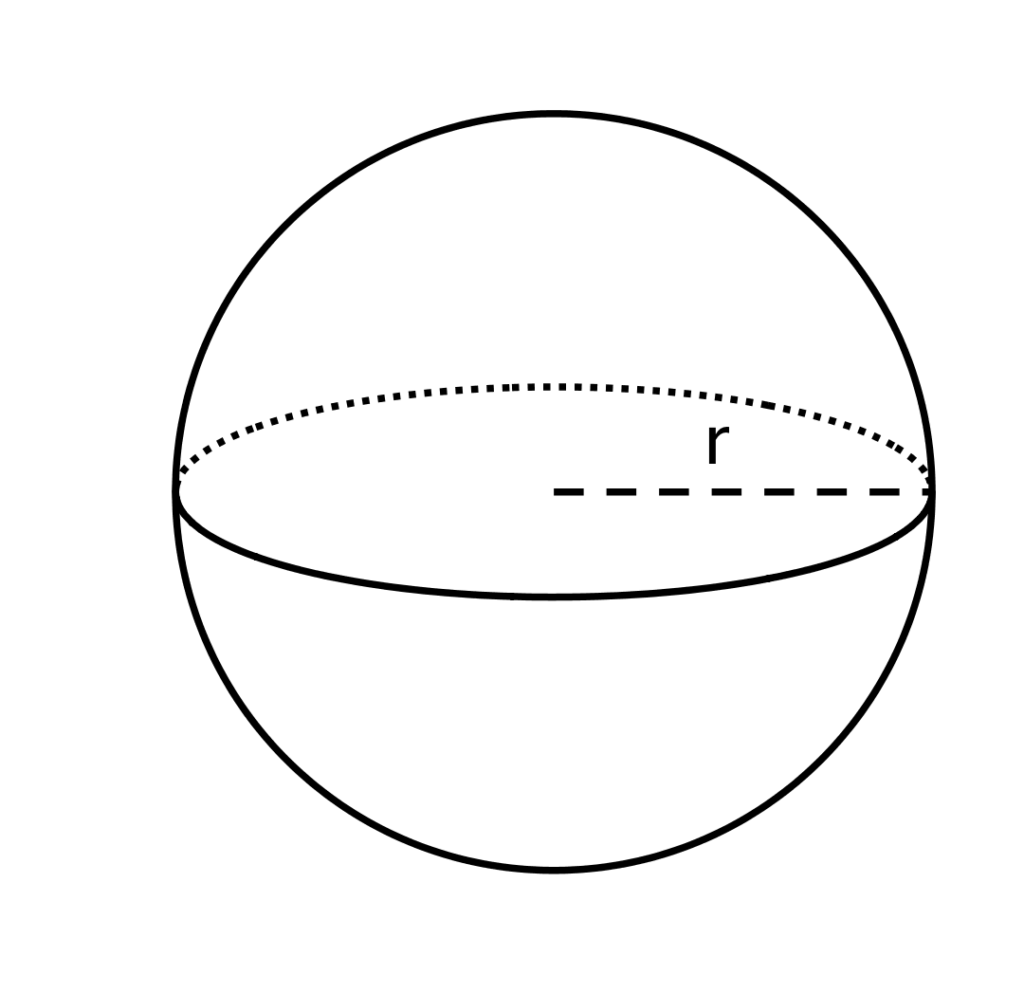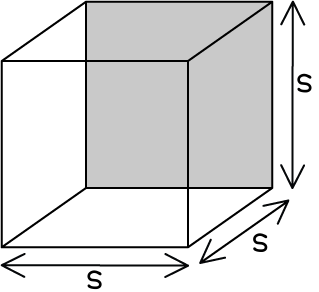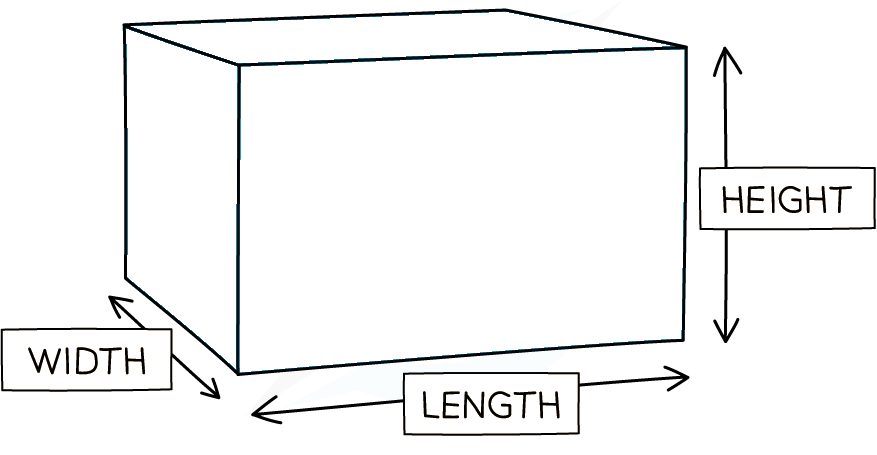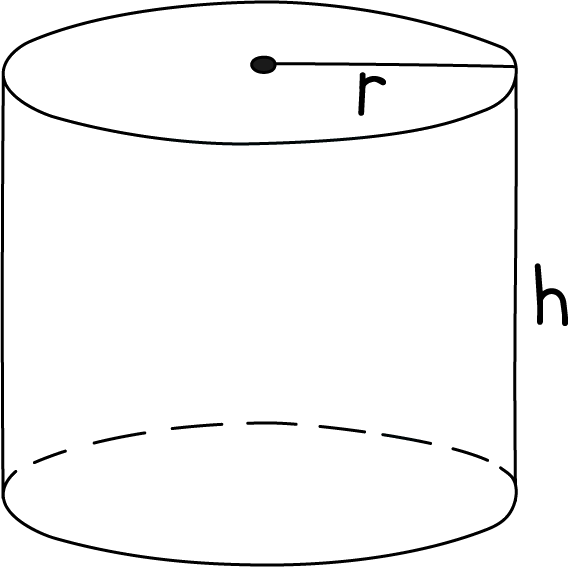Surface area		6s2	2lh + 2lw + 2wh
Volume		s3	l × w × h
Example	If r = 1 cm SA = 4π(1)2 = 4π cm2 V = 4/3 πr3 = 4/3 π13 =  4/3 π  ∴ SA:V ratio = 4:4/3 = 3:1	If s = 1 cm then SA = (1×1)×6 SA = 6cm2 V = s3 = 13 =1cm3 ∴ SA:V ratio = 6:1	If l = 4cm, w = 2cm, h = 1cm, then SA = 2((4×1)+(4×2)+(2×1)) = 28cm2 V = 4 × 2 × 1 = 8cm3 ∴ SA:V ratio = 28:8 = 3.5:1	If r = 2 cm and h = 6cm, then SA = 2πrh + 2πr2 = 8π +24π = 32π cm2 V = π(2)2 × 6 = 24π cm2 ∴ SA : V ratio = 32 : 24 = 1.33:1

Maximizing surface area-to-volume ratio

• As cells increase in size, their surface area–to–volume (SA:V) ratio decreases and their metabolic requirements increase

  • This means that larger cells have proportionally less surface available for exchange of substances, relative to their greater internal demand

  • The maximum size to which single cells can grow is restricted by this relationship

• The surface area of the plasma membrane must be large enough to adequately exchange materials, so larger cells may have complex cellular structures, such as membrane folds, to enable adequate exchange of materials with the environment

Cell feature	Role	Adaptation for adequate exchange with environment
Root hairs	Root hairs are single-celled extensions found on epidermis cells in plant roots They aid absorption of water and minerals from the soil	Root hairs increase the surface area of plant roots, so increasing the rate at which water and minerals can be absorbed
Opening and closing guard cells	Guard cells surround stomata on the lower surface of a leaf, where their role is to open and close the stomata This allows plants to carry out gas exchange while also controlling water loss	Guard cells can become turgid, expanding and curving outwards to allow stomata to open This allows gases to diffuse into the leaf, where they come into contact with the large surface area of the spongy mesophyll
Microvilli on gut epithelial cells	Gut epithelial cells are located on the inside surface of the small intestine Their role is to absorb nutrients for distribution around the rest of the body	The surface area of the food-contacting surface is maximized by folded structures called microvilli
Cilia	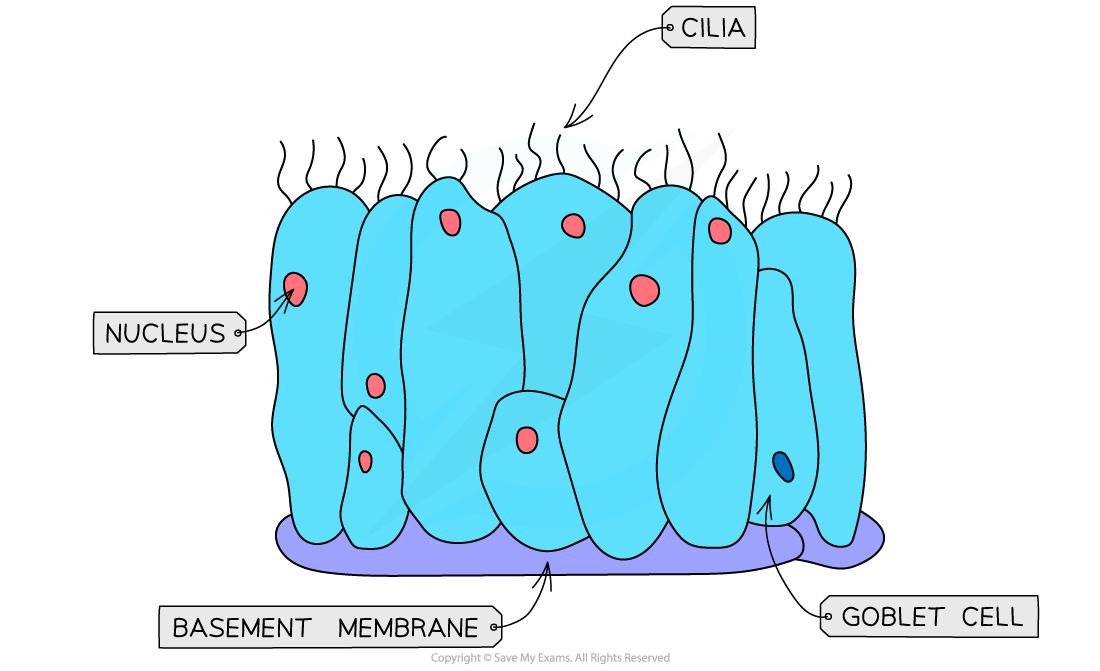Cilia are hair-like projections on cell surfaces that can beat to move fluid over the surface of cells, e.g. unicellular eukaryotes living in a watery environment may have many cilia	Cilia keep the fluid next to the surface of cells moving, bringing in fresh fluid; this maintains a steep concentration gradient and increases the rate of diffusion

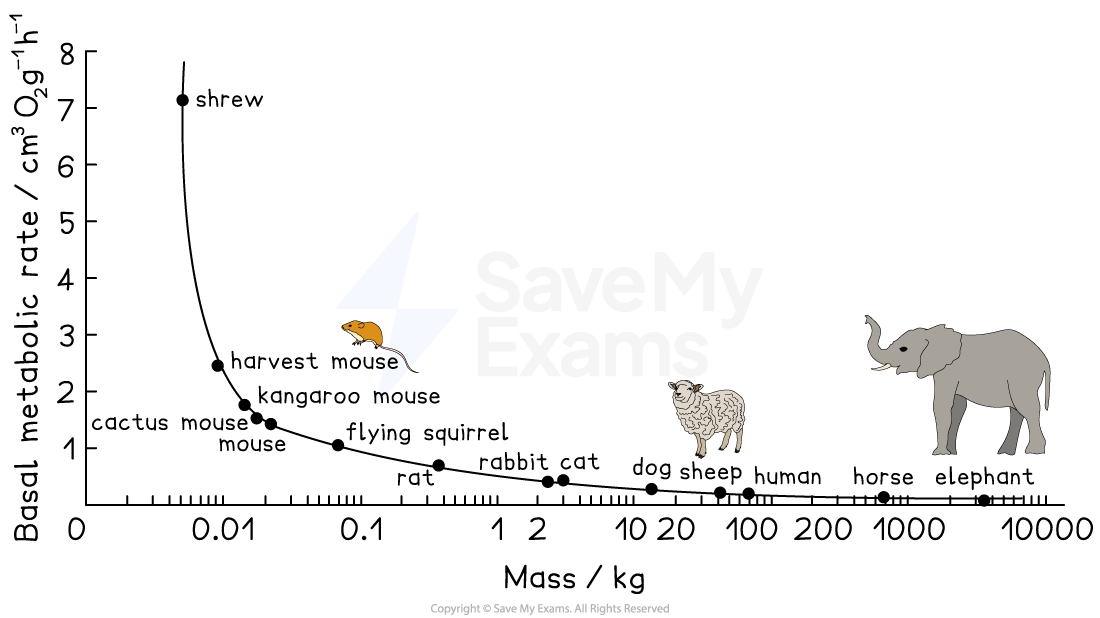
Surface area and heat exchange

• The rate of heat exchange with the environment is also affected by cell size

  • As cell mass increases, SA:V decreases, and the rate of heat exchange with the ambient environment also decreases

• Because of the relationship between SA:V and heat exchange, there is a also a relationship between metabolic rate per unit body mass and the size of multicellular organisms; this can be explained as follows:

  • small animals, with a higher SA:V ratio, will lose more heat to their surroundings, meaning that they need a relatively high metabolic rate to maintain body temperature

  • large animals, with a lower SA:V ratio, will lose less heat, meaning that they can maintain body temperature at a relatively low metabolic rate