Determining Rates of Reaction (SQA National 5 Chemistry): Revision Note
Exam code: X813 75
Average rate of reaction
The rate of a reaction tells us how fast a reaction is
The speed of a reaction changes over time
It's fastest at the start and slows down
So, we often measure the average rate over a specific time period
The average rate of reaction is the change in the amount of a reactant or product over a period of time
The average rate of reaction formula
The average rate of reaction is calculated using a formula from the SQA Chemistry Data Booklet:
average rate =
Average rate is the speed of the reaction over a certain time period
Δquantity is the change in quantity
This is calculated by:
Δquantity = final quantity - initial quantity
Δt is the change in time.
This is calculated by:
Δt = final time - initial time
Working out the units
The units for the rate depend on the units used in the experiment
You work them out by simply putting the quantity unit "per" the time unit
For example:
If you measure volume in cm3 and time in s, the rate unit is cm3 s-1
If you measure mass in g and time in s, the rate unit is g s-1
Calculating average rate from a graph
Worked Example
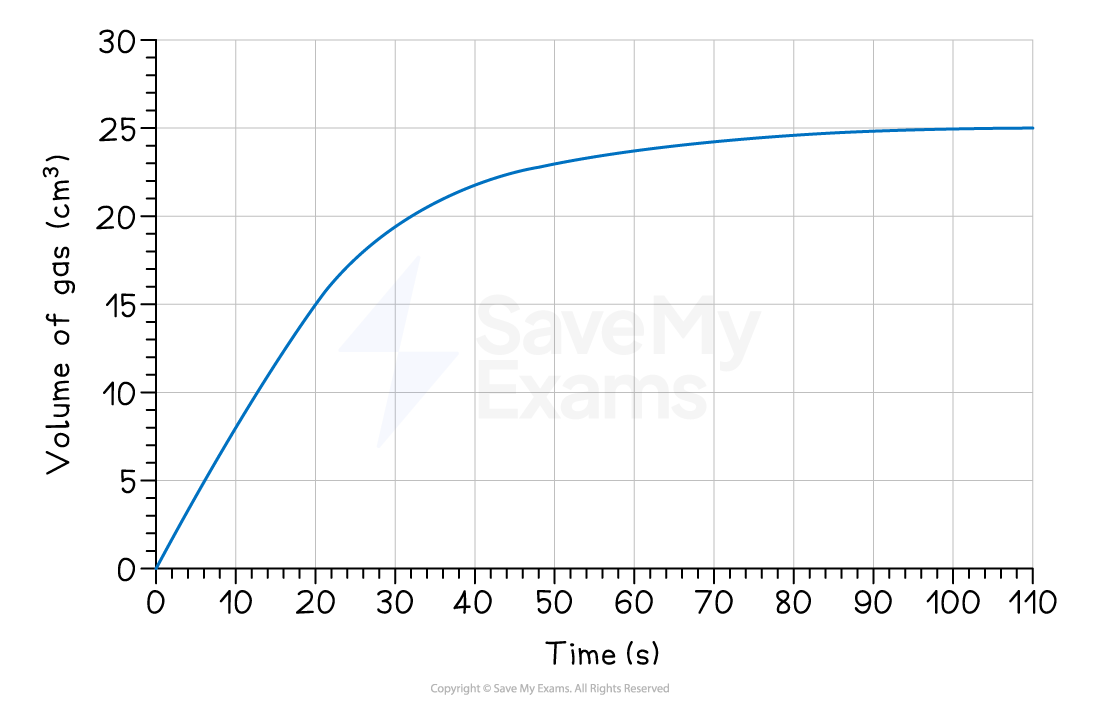
Using the graph below, calculate the average rate of reaction, in cm3 s-1, for the first 20 seconds.
[2]
Answer:
Write the formula:
average rate =
Find the quantity and time values from the graph:
At t = 0 s, the volume = 0 cm3
AND
At t = 20 s, the volume = 15 cm3
Calculate each change (Δ):
Δquantity = 15 - 0 = 15 cm3
Δt = 20 - 0 = 20 s
Substitute into the formula and solve:
average rate =
[1 mark]
average rate = 0.75 cm3 s-1
[1 mark]
Examiner Tips and Tricks
An exam question might give you the rate and ask you to find the quantity or time.
Remember the formula triangle to help you rearrange the equation:
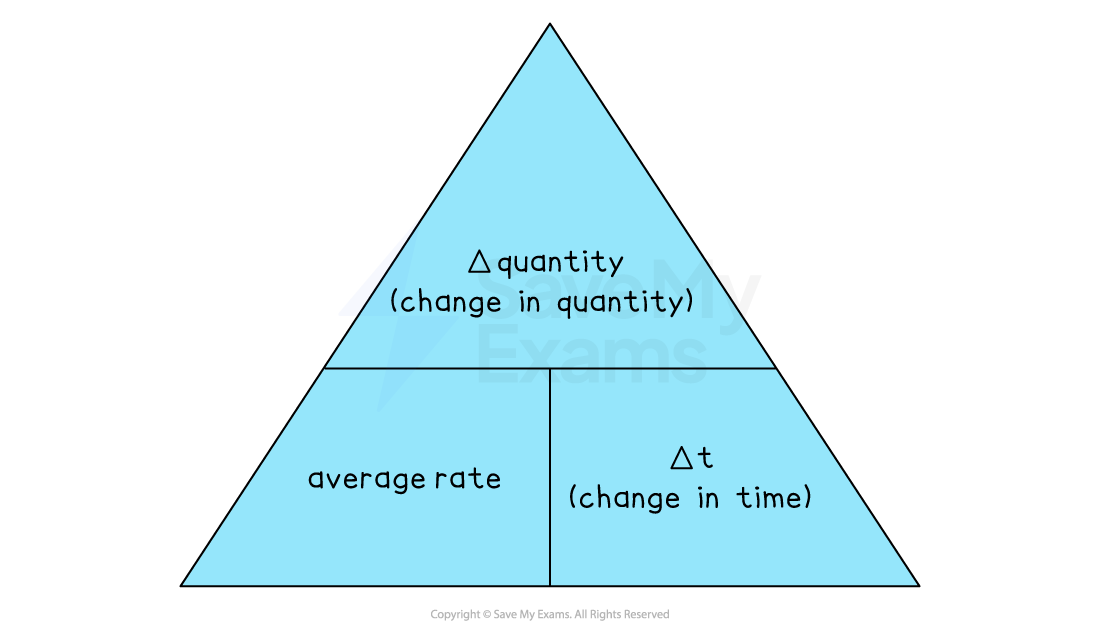
Δquantity = average rate x Δt
Δt =
Rates of Reaction over Time
The rate of a chemical reaction is not constant
By calculating the average rate at different stages, we can prove that a reaction slows down over time
Why the rate changes
A reaction's speed changes as it progresses:
At the start:
The rate is fastest
The concentration of reactants is high
So, the collisions are more frequent
In the middle:
The rate slows down
The reactants are being used up
So, collisions become less frequent
At the end:
The rate is zero
A reactant has run out
So, the reaction stops
Proving the rate decreases
We can use a reaction-rate graph to calculate the average rate during different periods of the reaction
This mathematically proves that the reaction slows down
Worked Example
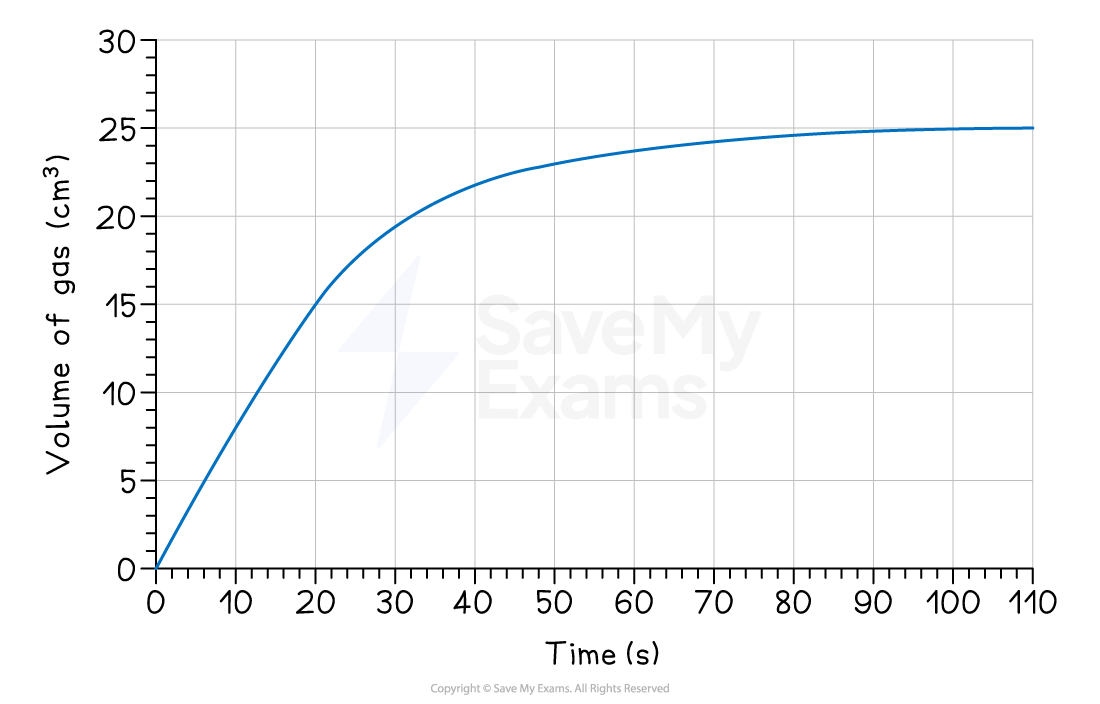
Using the graph below, compare the rate in the first 20 seconds to the rate between 20 and 40 seconds.
[3]
Calculate the rate for the first 20 seconds (0 s to 20 s):
Δquantity = 15 - 0 = 15 cm3
Δt = 20 - 0 = 20 s
average rate = = 0.75 cm3 s-1
[1 mark]
Calculate the rate between 20 seconds and 40 seconds:
From the graph, at 40 s the volume is 22.5 cm³.
Δquantity = 22.5 - 15 = 7.5 cm3
Δt = 40 - 20 = 20 s
average rate = = 0.375 cm3 s-1
[1 mark]
Conclusion:
Since 0.75 cm3 s-1 (the rate from 0 - 20 s) is greater than 0.375 cm3 s-1 (the rate from 20 - 40 s), this proves that the rate of reaction decreases over time.
[1 mark]

Unlock more, it's free!
Did this page help you?