Born-Haber Cycle Calculations (HL) (DP IB Chemistry)
Revision Note
Born-Haber Cycle Calculations
Once a Born-Haber cycle has been constructed, it is possible to calculate the lattice enthalpy (ΔHlatꝋ) by applying Hess’s law and rearranging:
ΔHꝋf = ΔHꝋat + ΔHꝋat + IE + EA - ΔHꝋlat
If we simplify this into three terms, this makes the equation easier to see:
ΔHꝋlat
ΔHꝋf
ΔHꝋ1 (the sum of all of the various enthalpy changes necessary to convert the elements in their standard states to gaseous ions)
The simplified equation becomes:
ΔHꝋf = ΔHꝋ1 - ΔHꝋlat
So, if we rearrange to calculate the lattice enthalpy, the equation becomes
ΔHꝋlat = - ΔHꝋf + ΔHꝋ1
When calculating the ΔHlatꝋ, all other necessary values will be given in the question
A Born-Haber cycle could be used to calculate any stage in the cycle
For example, you could be given the lattice enthalpy and asked to calculate the enthalpy change of formation of the ionic compound
The principle would be exactly the same
Work out the direct and indirect route of the cycle (the stage that you are being asked to calculate will always be the direct route)
Write out the equation in terms of enthalpy changes and rearrange if necessary to calculate the required value
Remember: sometimes a value may need to be doubled or halved, depending on the ionic solid involved
For example, with MgCl2 the value for the first electron affinity of chlorine would need to be doubled in the calculation, because there are two moles of chlorine atoms
Therefore, you are adding 2 moles of electrons to 2 moles of chlorine atoms, to form 2 moles of chloride ions, i.e. 2Cl-
Worked Example
Calculating the lattice enthalpy of KCl
Given the data below, calculate the ΔHꝋlat of potassium chloride (KCl).
| ΔHꝋat (kJmol-1) | IE / EA (kJmol-1) |
|---|---|---|
K | +90 | +418 |
Cl | +122 | -349 |
ΔHꝋf (kJmol-1) | ||
KCl | -437 | |
Answer:
Step 1: Construct the Born-Haber cycle
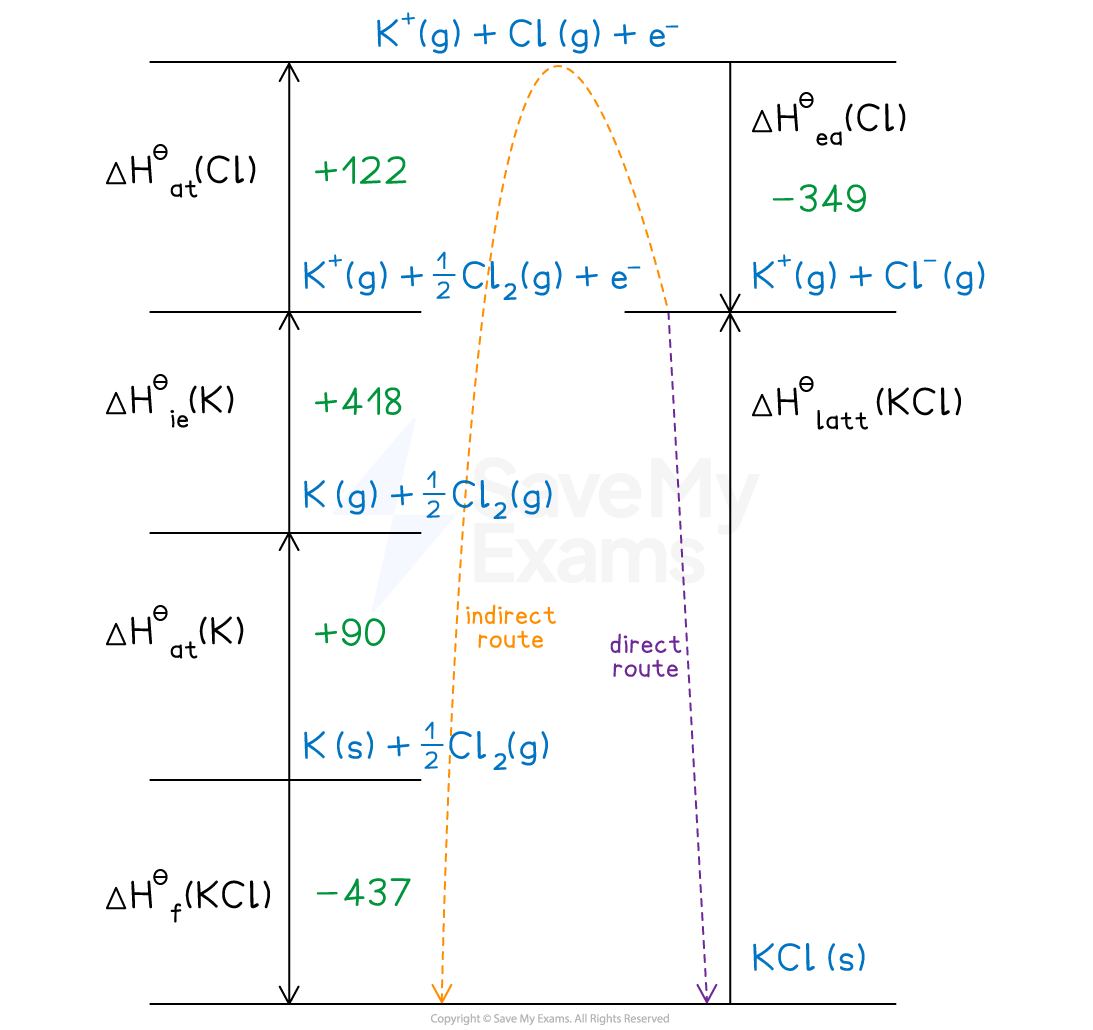
Step 2: Applying Hess’ law, the lattice enthalpy of KCl is:
ΔHꝋlat = -ΔHꝋf + ΔHꝋ1
ΔHꝋlat = -ΔHꝋf + [(ΔHꝋat K) + (ΔHꝋat Cl) + (IE1 K) + (EA1 Cl)]
Step 3: Substitute in the numbers:
ΔHꝋlat = -(-437) + [(+90) + (+122) + (+418) + (-349)] = 718 kJ mol-1
Worked Example
Calculating the lattice enthalpy of MgO
Given the data below, calculate the of ΔHꝋlat magnesium oxide of magnesium oxide (MgO)
| ΔHꝋat (kJmol-1) | IE1 / EA1(kJmol-1) | IE1 / EA1(kJmol-1) |
|---|---|---|---|
Mg | +148 | +736 | +1450 |
O | +248 | -142 | +770 |
ΔHꝋf (kJmol-1) | |||
MgO | -602 | ||
Answer:
Step 1: Construct the Born-Haber cycle
Step 2: Applying Hess’ law, the lattice enthalpy of MgO is:
ΔHꝋlat = -ΔHꝋf + ΔHꝋ1
ΔHꝋlat = -ΔHꝋf + [(ΔHꝋat Mg) + (ΔHꝋat O) + (IE1 Mg) + (IE2 Mg) + (EA1 O) + (EA2 O)]
Step 3: Substitute in the numbers:
ΔHꝋlat = -(-602) + [(+148) + (+248) + (+736) + (+1450) + (-142) + (+770)]
= 3812 kJ mol-1
You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?