Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)SLRevision Notes5. CalculusDifferentiationGradients, Tangents & Normals

Gradients, Tangents & Normals (DP IB Analysis & Approaches (AA)): Revision Note

Paul

Written by: Paul

Reviewed by: Dan Finlay

Updated on

DP Analysis & Approaches (AA): SLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): SLDP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): SLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): SLDP Applications & Interpretation (AI): SL

Did this video help you?

Finding Gradients

How do I find the gradient of a curve at a point?

  • The gradient of a curve at a point is the gradient of the tangent to the curve at that point

  • Find the gradient of a curve at a point by substituting the value of bold italic x at that point into the curve's derivative function

  • For example, if f open parentheses x close parentheses equals x squared plus 3 x minus 4

    • then f to the power of apostrophe open parentheses x close parentheses equals 2 x plus 3

    • So the gradient of y equals f open parentheses x close parentheses when x equals 1 is  f to the power of apostrophe open parentheses 1 close parentheses equals 2 open parentheses 1 close parentheses plus 3 equals 5

    • and the gradient of y equals f open parentheses x close parentheses when x equals negative 2 is  f to the power of apostrophe open parentheses negative 2 close parentheses equals 2 open parentheses negative 2 close parentheses plus 3 equals negative 1

  • Although your GDC won't find a derivative function for you, it is possible to use your GDC to find the value of the derivative of a function at a point, using fraction numerator d over denominator d x end fraction open parentheses space box enclose space space space space space space space space end enclose space close parentheses subscript x equals box enclose blank end enclose end subscript

Worked Example

A function is defined by f open parentheses x close parentheses equals x cubed plus 6 x squared plus 5 x minus 12.

(a) Find f to the power of apostrophe open parentheses x close parentheses.

Vx0rvphg_rn-we-5-1-2-ib-ai-sl-finding-gradiens-parta

(b) Hence show that the gradient of y equals f open parentheses x close parentheses when x equals 1 is 20.

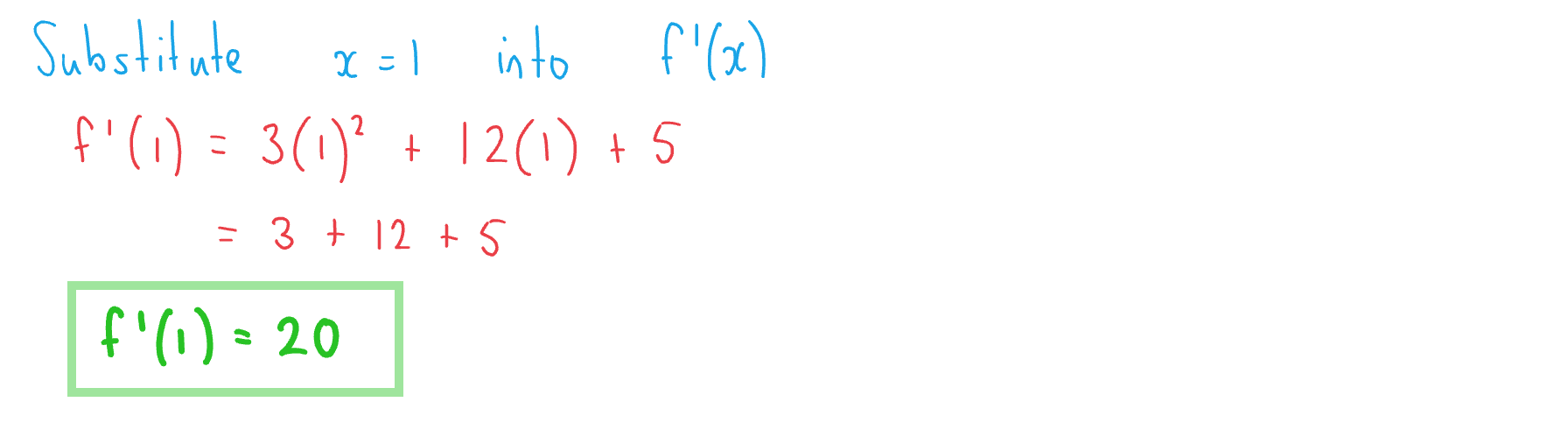
ksEAxyN__rn-we-5-1-2-ib-ai-sl-finding-gradiens-partb

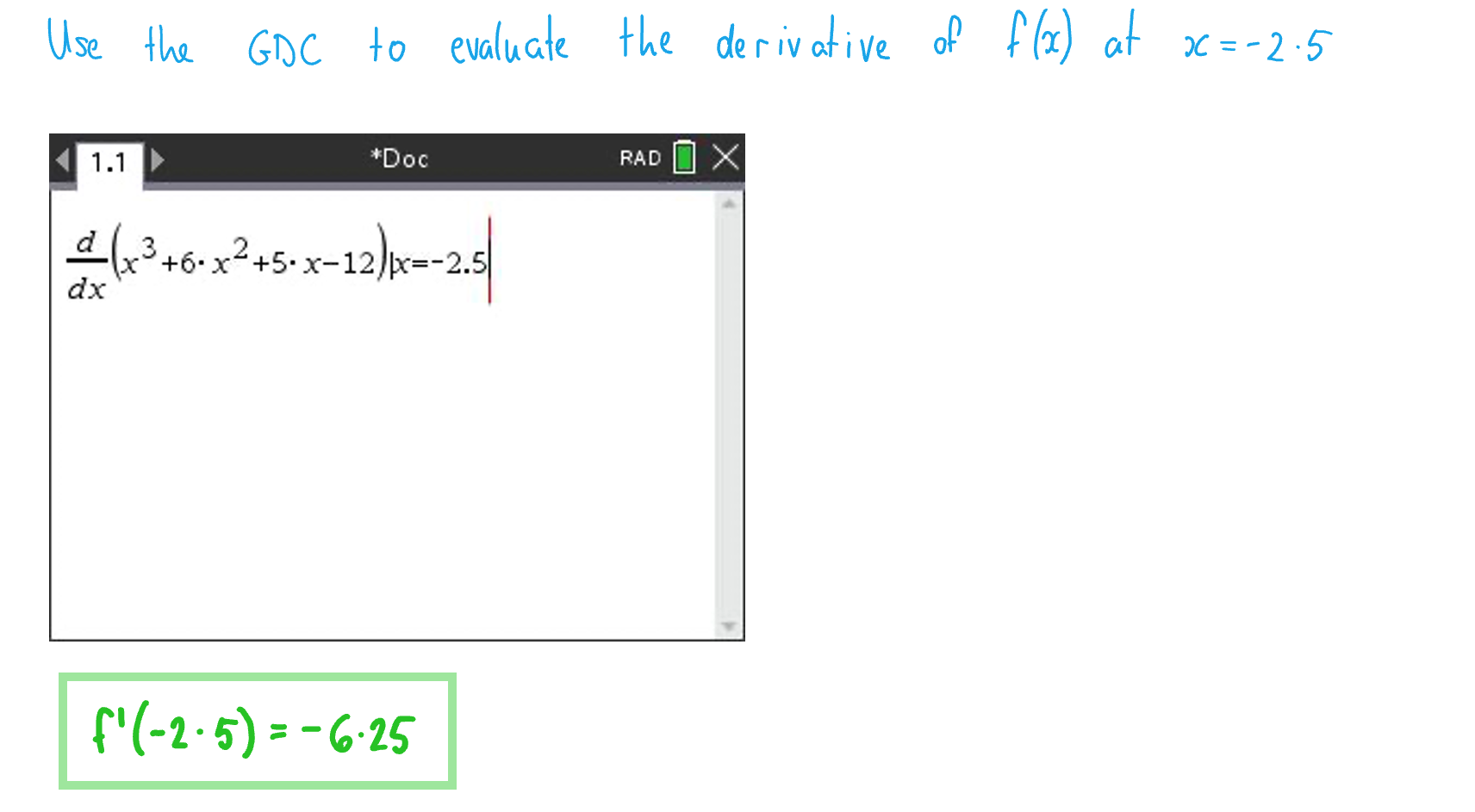
(c) Find the gradient of y equals f open parentheses x close parentheses when x equals negative 2.5.

3T8SSV-9_rn-we-5-1-2-ib-ai-sl-finding-gradiens-partc

Did this video help you?

Tangents & Normals

What is a tangent?

  • At any point on the graph of a (non-linear) function, the tangent is the straight line that touches the graph at the point without crossing through the graph

  • Its gradient is given by the derivative function

Graph of a curve y=f(x) with a red tangent line at a point marked in red on the curve, demonstrating the concept of tangency and gradient in calculus.

How do I find the equation of a tangent?

  • To find the equation of a straight line, a point and the gradient are needed

  • The gradient, m, of the tangent to the function y equals f open parentheses x close parentheses at left parenthesis x subscript 1 comma blank y subscript 1 right parenthesis is Error converting from MathML to accessible text.

  • To find the equation of the tangent to the function y equals f left parenthesis x right parenthesis at the point left parenthesis x subscript 1 comma blank y subscript 1 right parenthesis

    • substitute the gradient, f to the power of apostrophe open parentheses x subscript 1 close parentheses and point left parenthesis x subscript 1 comma blank y subscript 1 right parenthesis

    • into the equation of a line y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses

    • This gives:

      •  y minus y subscript 1 equals f to the power of apostrophe stretchy left parenthesis x subscript 1 stretchy right parenthesis left parenthesis x minus x subscript 1 right parenthesis

Examiner Tips and Tricks

You could also substitute into y equals m x plus c, but it is usually quicker to substitute into y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses.

What is a normal?

  • At any point on the graph of a (non-linear) function, the normal is the straight line that passes through that point and is perpendicular to the tangent

Graph showing a curve y = f(x) with a tangent line in red and normal line in green at a point of contact, forming a right angle.

How do I find the equation of a normal?

  • The gradient of the normal to the function y equals f open parentheses x close parenthesesat left parenthesis x subscript 1 comma blank y subscript 1 right parenthesis is Error converting from MathML to accessible text.

  • Therefore find the equation of the normal to the function y equals f left parenthesis x right parenthesis at the point left parenthesis x subscript 1 comma blank y subscript 1 right parenthesis by using

    • y minus y subscript 1 equals fraction numerator negative 1 over denominator f to the power of apostrophe stretchy left parenthesis x subscript 1 stretchy right parenthesis end fraction left parenthesis x minus x subscript 1 right parenthesis

Examiner Tips and Tricks

You are not given the formulas for the equation of a tangent or the equation of a normal.

However both can be derived from the equations of a straight line which are given in the formula booklet.

Worked Example

The function f left parenthesis x right parenthesis is defined by

 f stretchy left parenthesis x stretchy right parenthesis equals 2 x to the power of 4 plus 3 over x squared blank x not equal to 0

a) Find an equation for the tangent to the curve y equals straight f left parenthesis x right parenthesis at the point where x equals 1, giving your answer in the form y equals m x plus c.

5-1-2-ib-sl-ai-aa-we2-soltn-a

b) Find an equation for the normal at the point where x equals 1, giving your answer in the form a x plus b y plus d equals 0, where a, b and d are integers.

5-1-2-ib-sl-ai-aa-we2-soltn-b

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Differentiating Powers of xNext:Increasing & Decreasing Functions
    Author
    Reviewer
    Paul

    Author: Paul

    Expertise: Maths Content Creator

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.