Acid & Base Dissociation Constants (HL) (DP IB Chemistry): Revision Note

Acid & base dissociation constants

Weak acids

• A weak acid is an acid that partially (or incompletely) dissociates in aqueous solutions

  • Examples; most carboxylic acids (e.g. ethanoic acid), HCN (hydrocyanic acid), H₂S (hydrogen sulfide) and H₂CO₃ (carbonic acid)

• In general, the following equilibrium is established:

HA (aq) + H₂O (l) ⇌  A^- (aq) + H₃O⁺ (aq)

OR

HA (aq) ⇌  A^- (aq) + H⁺ (aq)

• At equilibrium:

  • Most HA molecules remain undissociated

  • The position lies to the left

  • An equilibrium constant can be written from this equation

• This constant is called the acid dissociation constant, K_a

• Carboxylic acids are weak acids

  • For example, propanoic acid, CH₃CH₂COOH (aq), dissociates according to the following equation which leads to the K_a expression for propanoic acid:

CH₃CH₂COOH (aq) + H₂O (l) ⇌ CH₃CH₂COO^– (aq) + H₃O⁺ (aq)

OR

CH₃CH₂COOH (aq) ⇌ CH₃CH₂COO^– (aq) + H⁺ (aq)

• The acid dissociation constant expressions for propanoic acid:

• Values of K_a are very small

  • The K_a  for propanoic acid = 1.34 x 10^-5 

  • When writing the equilibrium expression for weak acids, we assume that the concentration of H⁺ (aq)  due to the ionisation of water is negligible

Weak bases

• A weak base only partially ionises in water.

  • This ionisation is described by the base dissociation constant K_b

• In general, the equilibrium established is:

B (aq) + H₂O (l) ⇌  BH⁺ (aq) + OH^- (aq)

• The base dissociation constant expression is:

• Amines are weak bases

  • For example, 1-phenylmethanamine, C₆H₅CH₂NH₂ (aq), dissociates according to the following equation which leads to the K_a expression for 1-phenylmethanamine:

C₆H₅CH₂NH₂ (aq) + H₂O (l) ⇌ C₆H₅CH₂NH₃⁺ (aq) + OH^- (aq)

• Base dissociation constant expression for 1-phenylmethanamine

pK_a and pK_b 

• The range of values of K_a and K_b is very wide

• For weak acids, the values themselves are very small numbers

Table of K_a values

• For this reason, it is easier to work with another term called pK_a for acids or pK_b for bases

• In order to convert the values we need to apply the following calculations:

pK_a = -logK_a                 K_a= 10^-pK_a

pK_b = -logK_b                 K_b= 10^-pK_b

• The range of pK_a values for most weak acids lies between 3 and 7

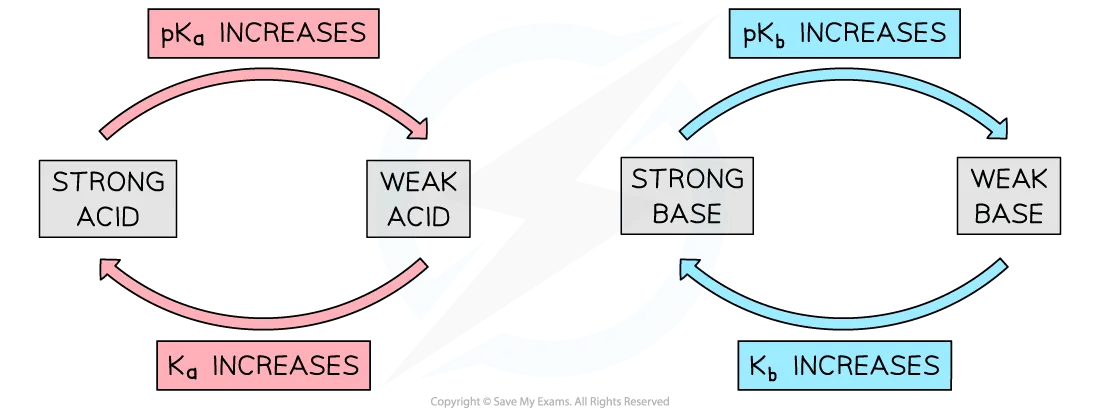
Relative strengths of acids and bases

• A larger K_a value = stronger acid

• A larger pK_a = weaker acid

• A larger K_b value = stronger base

• A larger pK_b value = weaker base

Diagram showing the relationship between strong and weak acids / bases

• In all aqueous solutions, an equilibrium exists in water where a few water molecules dissociate into protons and hydroxide ions

• We can derive an equilibrium constant for the reaction:

H₂O (l) ⇌ H⁺ (aq) + OH^- (aq)

• The concentration of water is constant, so the expression for K_w is:

K_w = [H⁺][OH^-]

• This is a specific equilibrium constant called the ion product for water

• The product of the two ion concentrations is 1.00 x 10^-14  at 298 K

• For conjugate acid-base pairs, K_a and K_b are related to K_w

K_a x K_b = K_w

• The conjugate base of ethanoic acid is the ethanoate ion, CH₃COO^– (aq) 

   CH₃COOH (aq)  ⇌ CH₃COO^– (aq) + H⁺ (aq)

acid                 conjugate base

• We can then put this into the K_a expression

• The ethanoate ion will react with water according to the following equation

CH₃COO^– (aq) + H₂O (l) ⇌ CH₃COOH (aq) + OH^- (aq)

• We can then put this into the K_b expression

• Now, these two expressions can be combined, which corresponds to

K_a x K_b = K_w

K_a x K_b = 10^-14

• Or we could say that

pK_a + pK_b = pK_w

pK_a + pK_b = 14

• This makes the numbers much easier to deal with as using K_a K_b = 10^-14 will give very small numbers

• Combining the K_a and K_b expressions:

• Or rearranging: