Stationary Points (DP IB Applications & Interpretation (AI)): Revision Note

Stationary Points & Turning Points

What is the difference between a stationary point and a turning point?

• A stationary point is a point at which a function's gradient function is equal to zero

  • The tangent to the curve of the function is horizontal

• A turning point is a type of stationary point

  • But in addition the function changes at a turning point

    • from increasing to decreasing

    • or from decreasing to increasing

  • The curve ‘turns’ from ‘going upwards’ to ‘going downwards’ or vice versa

  • Turning points will either be (local) minimum or maximum points

• A point of inflection could also be a stationary point but is not a turning point

How do I find stationary points and turning points?

• For the function , stationary points (including turning points) can be found using the following process
   

• STEP 1

  Find the gradient function,
   

• STEP 2

  Solve the equation to find the -coordinate(s) of any stationary points

  • Remember that turning points are a type of stationary point
     

• STEP 3

  If the-coordinates of the stationary points are also required then substitute the-coordinate(s) into

Testing for Local Minimum & Maximum Points

What are local minimum and maximum points?

• Local minimum and maximum points are two types of stationary point

  • The gradient function (derivative) at such points equals zero

  • i.e. 

• A local minimum point, will be the lowest value of in the local vicinity of the value of

  • The function may reach a lower value further away from the point

• Similarly, a local maximum point,  will be the highest value of in the local vicinity of the value of

  • The function may reach a greater value further away from the point

• The nature of a stationary point refers to whether it is a local minimum point, a local maximum point or a point of inflection

• A global minimum point would represent the lowest value of for all values of

  • similar for a global maximum point

How do I find local minimum & maximum points?

• The nature of a stationary point can be determined using the first derivative but it is usually quicker and easier to use the second derivative

  • The first derivative method is only needed in cases where the second derivative is zero

• For the function...
   

• STEP 1

  Find  and solve to find the -coordinates of any stationary points
   

• STEP 2 (Second derivative)

  Find  and evaluate it at each of the stationary points found in STEP 1
   

• STEP 3 (Second derivative)

  • If  then the nature of the stationary point cannot be determined; use the first derivative method (STEP 4)

  • If  then the curve of the graph of is concave up and the stationary point is a local minimum point

  • If then the curve of the graph of is concave down and the stationary point is a local maximum point

• STEP 4 (First derivative)

  Find the sign of the first derivative just either side of the stationary point;  i.e. evaluate and for small
   

  • At a local minimum point the function changes from decreasing to increasing

    • the gradient changes from negative to positive

    • 

  • At a local maximum point the function changes from increasing to decreasing

    • the gradient changes from positive to negative

    • 

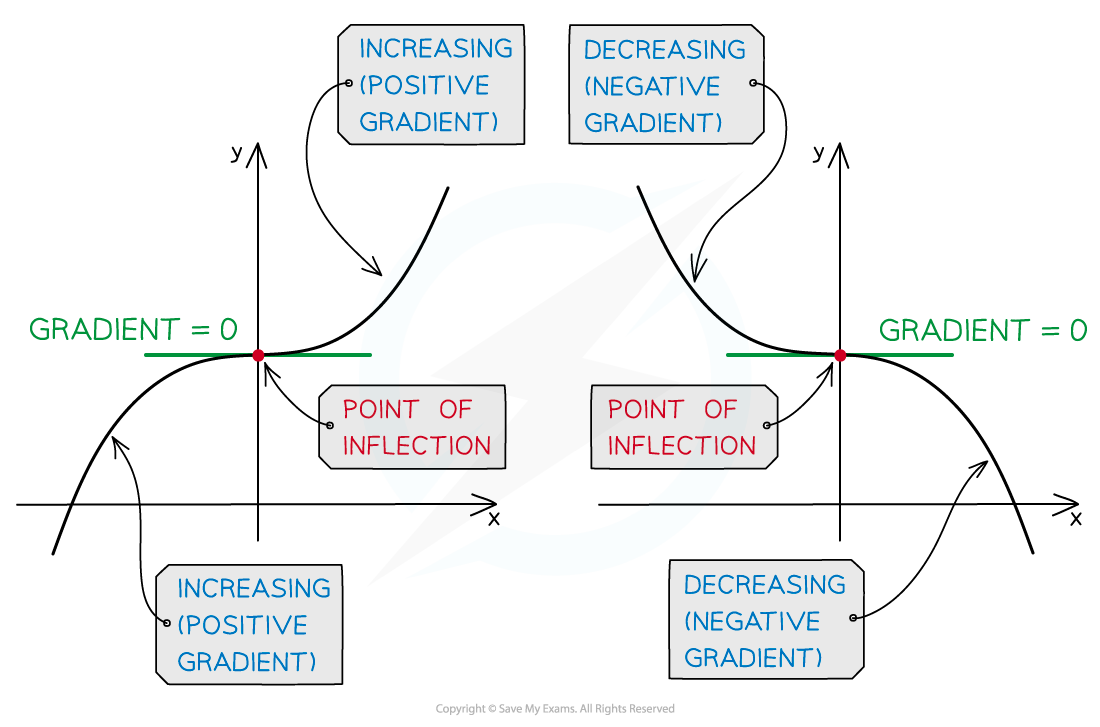
  • At a stationary point of inflection the function remains either increasing or decreasing on both sides of the stationary point

    • the gradient does not change sign

    •    or  

    • a point of inflection does not necessarily have

      • This method will only find those that do

      • These are often called horizontal points of inflection