Equations of a Straight Line (DP IB Applications & Interpretation (AI)): Revision Note

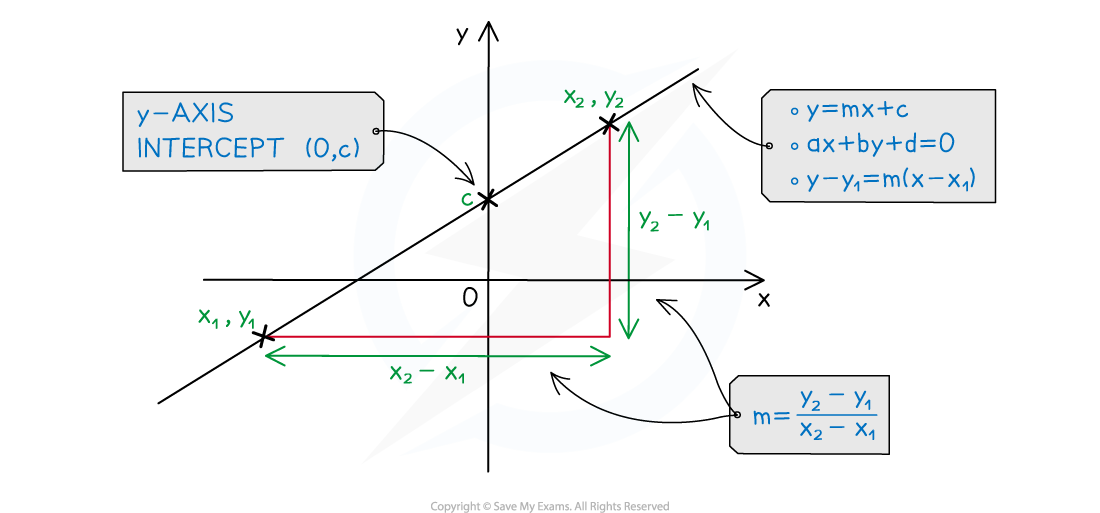
Equations of a Straight Line

How do I find the gradient of a straight line?

• Find two points that the line passes through with coordinates and 

• The gradient between these two points is

   

  • This is given in the formula booklet

• The gradient of a straight line measures its slope

  • A line with gradient 1 will go up 1 unit for every unit it goes to the right

  • A line with gradient -2 will go down two units for every unit it goes to the right

What are the equations of a straight line?

• 

  • This is the gradient-intercept form

  • It clearly shows the gradient and the -intercept

• 

  • This is the point-gradient form

  • It clearly shows the gradient and a point on the line

• 

  • This is the general form

  • You can quickly get the -intercept and -intercept

How do I find an equation of a straight line?

• You will need the gradient

  • If you are given two points then first find the gradient

• It is easiest to start with the point-gradient form,

  • Then rearrange into the required form

• If you have two points then you can use your GDC to find the equation

  • Enter the points in statistics mode and find the regression line