Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes3. Geometry & TrigonometryModelling with VectorsConstant & Variable Velocity

Constant & Variable Velocity (DP IB Applications & Interpretation (AI)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

Did this video help you?

Vectors & Constant Velocity

How can I model motion with constant velocity using vectors?

  • The formula for the position vector of an object is bold italic r equals bold italic r subscript 0 plus bold italic v t

    • bold italic r subscript 0 is the position vector of the starting point

    • bold italic v is the velocity for the constant velocity

    • t is the time since the object first left the starting point

  • An object moves in a straight line if the velocity is constant

Examiner Tips and Tricks

This formula is not given in the formula booklet. However, this is just the vector equation of a line where bold italic r subscript 0 is a point on the line of motion and bold italic v is the direction of motion.

Worked Example

A car, moving at constant speed, takes 2 minutes to drive in a straight line from point A (-4, 3) to point B (6, -5).

At time t, in minutes, the position vector (p) of the car relative to the origin can be given in the form bold italic p equals bold italic a plus t bold italic b. 

Find the vectors a and b.

3-10-2-ib-aa-hl-kinematics-vectors-we-solution

Did this video help you?

Vectors & Variable Velocity

How can I model motion with variable velocity using vectors?

  • Variable velocity is represented by a vector whose components are functions of time

    • bold italic v equals open parentheses fraction numerator v subscript 1 open parentheses t close parentheses over denominator v subscript 2 open parentheses t close parentheses end fraction close parentheses

  • This means the position vector and acceleration vector are also functions of time

    • bold italic r equals open parentheses fraction numerator r subscript 1 open parentheses t close parentheses over denominator r subscript 2 open parentheses t close parentheses end fraction close parentheses

    • bold italic a equals open parentheses fraction numerator a subscript 1 open parentheses t close parentheses over denominator a subscript 2 open parentheses t close parentheses end fraction close parentheses

What is the connection between displacement and velocity vectors?

  • Velocity is the rate of change of the position

    • bold italic v equals fraction numerator d bold italic r over denominator d t end fraction

  • Differentiate the position vector to find an expression for the velocity vector

    • open parentheses fraction numerator v subscript 1 open parentheses t close parentheses over denominator v subscript 2 open parentheses t close parentheses end fraction close parentheses equals open parentheses table row cell r subscript 1 apostrophe open parentheses t close parentheses end cell row cell r subscript 2 apostrophe stretchy left parenthesis t stretchy right parenthesis end cell end table close parentheses

  • Integrate the velocity vector to find an expression for the position vector

    • stretchy left parenthesis fraction numerator r subscript 1 stretchy left parenthesis t stretchy right parenthesis over denominator r subscript 2 stretchy left parenthesis t stretchy right parenthesis end fraction stretchy right parenthesis equals open parentheses table row cell integral v subscript 1 d t end cell row cell integral v subscript 2 d t end cell end table close parentheses

Examiner Tips and Tricks

Don't forget to include a constant of integration for each component. To find the full expression, you need to know the position vector of the object at a specific time. More information is given in the calculus section.

What is the connection between acceleration and velocity vectors?

  • Acceleration is the rate of change of the velocity

    • bold italic a equals fraction numerator d bold italic v over denominator d t end fraction

  • This means it is the second derivative of the position

    • bold italic a equals fraction numerator d squared bold italic r over denominator d t squared end fraction

  • Differentiate the velocity vector to find an expression for the acceleration vector

    • open parentheses fraction numerator a subscript 1 open parentheses t close parentheses over denominator a subscript 2 open parentheses t close parentheses end fraction close parentheses equals open parentheses table row cell v subscript 1 apostrophe open parentheses t close parentheses end cell row cell v subscript 2 apostrophe stretchy left parenthesis t stretchy right parenthesis end cell end table close parentheses

  • Differentiate the position vector twice to find an expression for the acceleration vector

    • open parentheses fraction numerator a subscript 1 open parentheses t close parentheses over denominator a subscript 2 open parentheses t close parentheses end fraction close parentheses equals open parentheses table row cell r subscript 1 apostrophe open parentheses t close parentheses end cell row cell r subscript 2 apostrophe stretchy left parenthesis t stretchy right parenthesis end cell end table close parentheses

  • Integrate the acceleration vector to find an expression for the velocity vector

    • stretchy left parenthesis fraction numerator v subscript 1 stretchy left parenthesis t stretchy right parenthesis over denominator v subscript 2 stretchy left parenthesis t stretchy right parenthesis end fraction stretchy right parenthesis equals open parentheses table row cell integral a subscript 1 d t end cell row cell integral a subscript 2 d t end cell end table close parentheses

Examiner Tips and Tricks

Don't forget to include a constant of integration for each component. To find the full expression, you need to know the velocity vector of the object at a specific time. Also, you can integrate the acceleration vector twice to find the position vector. You need to know the position vectors at two different times to find the full expression.

Worked Example

A ball is rolling down a hill with velocity bold italic v equals open parentheses 5 3 close parentheses plus t open parentheses space space space space 0 minus 0.8 close parentheses. At the time t equals 0 the position vector of the ball is 3 bold italic i minus 2 bold italic j.

a) Find the acceleration vector of the ball's motion.

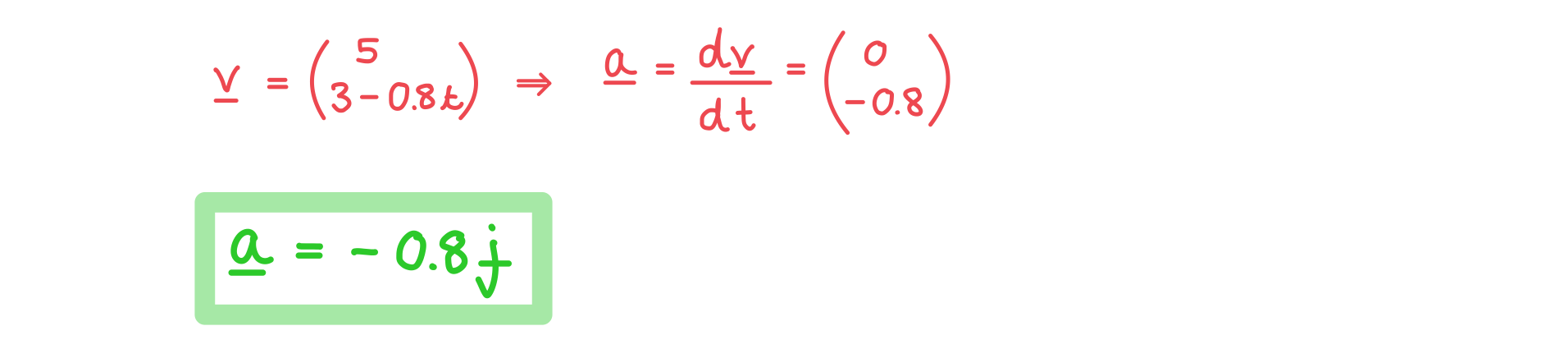
3-9-2-ib-ai-hl-variable-velocity-we-solution-a

b) Find the position vector of the ball at the time, t.

3-9-2-ib-ai-hl-variable-velocity-we-solution-b

 

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Kinematics with VectorsNext:Introduction to Graph Theory
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.