Poisson Distribution (DP IB Applications & Interpretation (AI)): Revision Note

Properties of Poisson distribution

What is a Poisson distribution?

• A Poisson distribution is a discrete probability distribution

• A discrete random variable  follows a Poisson distribution if it counts the number of occurrences in a fixed time period given the following conditions:

  • Occurrences are independent

  • Occurrences occur at a uniform average rate for the time period

• If  follows a Poisson distribution then it is denoted 

  • m is the average rate of occurrences for the time period

    • E.g., m might be 13.2 occurrences per hour

• The formula for the probability of r occurrences is given by:

  •   for r = 0,1,2,...

    • e is Euler’s constant 2.718...

    • and 

    • There is no upper bound for the number of occurrences

  • You will be expected to use the distribution function on your GDC to calculate probabilities with the Poisson distribution

What are the important properties of a Poisson distribution?

• The expected number (mean) of occurrences is m

  • You are given this in the exam formula booklet

• The variance of the number of occurrences is also m

  • You are given this in the exam formula booklet

  • Take the square root to get the standard deviation

• The mean and variance for a Poisson distribution are equal

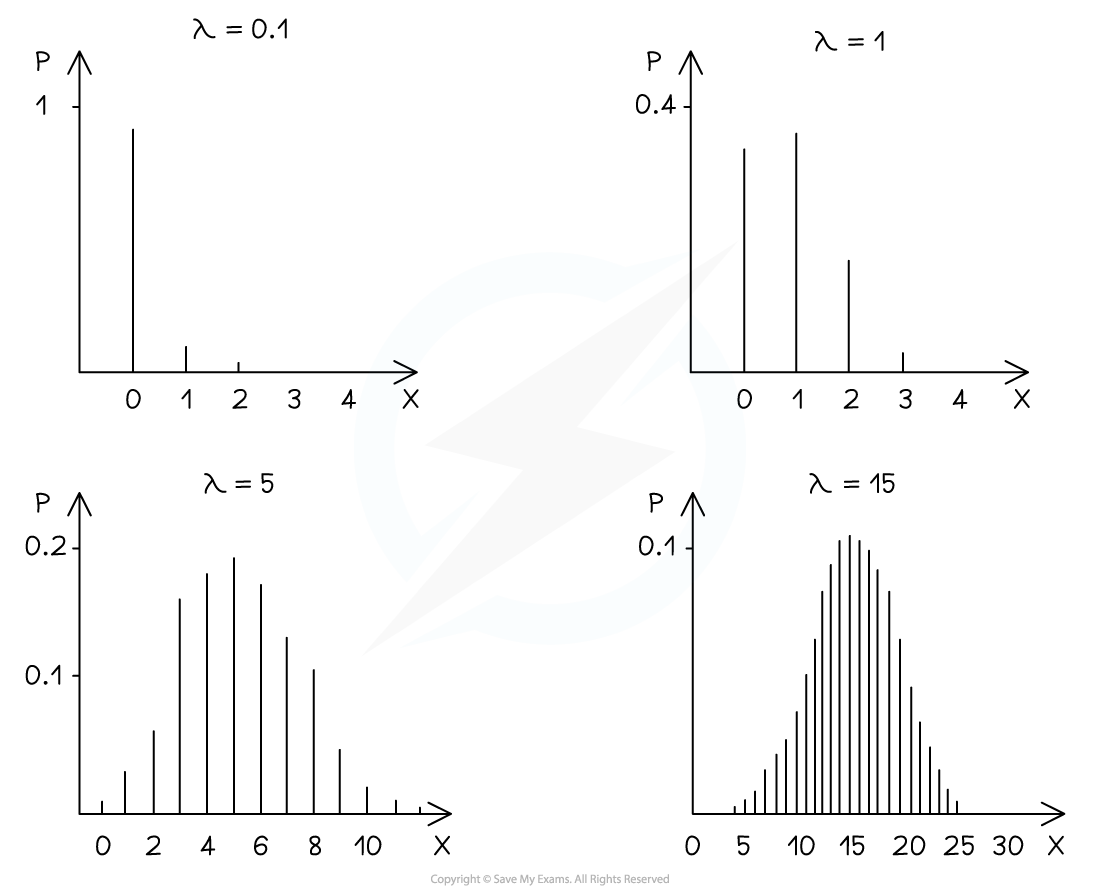
• The distribution can be represented visually using a vertical line graph

  • The graphs have tails to the right for all values of m

  • As m gets larger the graph gets more symmetrical

• If two Poisson variables  and  are independent then 

  • I.e. the sum of Poisson variables is also a Poisson variable

    • and its mean is the sum of the two means

  • This extends to n independent Poisson distributions 

    • 

Modelling with Poisson distribution

How do I set up a Poisson model?

• Identify what an occurrence is in the scenario

  • For example: a car passing a camera, a machine producing a faulty item

• Use proportion to find the mean number of occurrences for the given time period

  • For example: 10 cars in 5 minutes would be 120 cars in an hour if the Poisson model works for both time periods

• Make sure you clearly state what your random variable is

  • For example: let X be the number of cars passing a camera in 10 minutes

What can be modelled using a Poisson distribution?

• Anything that satisfies the two conditions

• For example, Let C be the number of calls that a helpline receives within a 15-minute period:  

  • An occurrence is the helpline receiving a call and can be considered independent

  • The helpline receives calls at an average rate of m calls during a 15-minute period

• Sometimes a measure of space will be used instead of a time period

  • For example, the number of daisies that exist on a square metre of grass

• If the mean and variance of a discrete variable are (approximately) equal then it might be possible to use a Poisson model