National 5PhysicsSQARevision NotesProperties Of MatterGas Laws & The Kinetic ModelThe Gas Laws

The Gas Laws (SQA National 5 Physics): Revision Note

Exam code: X857 75

Leander Oates

Written by: Leander Oates

Reviewed by: Caroline Carroll

Updated on

The gas laws

  • The gas laws are a set of three laws that describe the relationships between the temperature, pressure and volume of gases

Pressure & volume

  • Pressure is inversely proportional to volume

p space equals space 1 over V

  • Where:

    • p = pressure in pascals (Pa)

    • V = volume in metres cubed (m3)

  • This means that:

p V space equals space constant

  • The pressure-volume relationship only works when:

    • the gas is at a constant temperature

    • the mass of the gas does not change

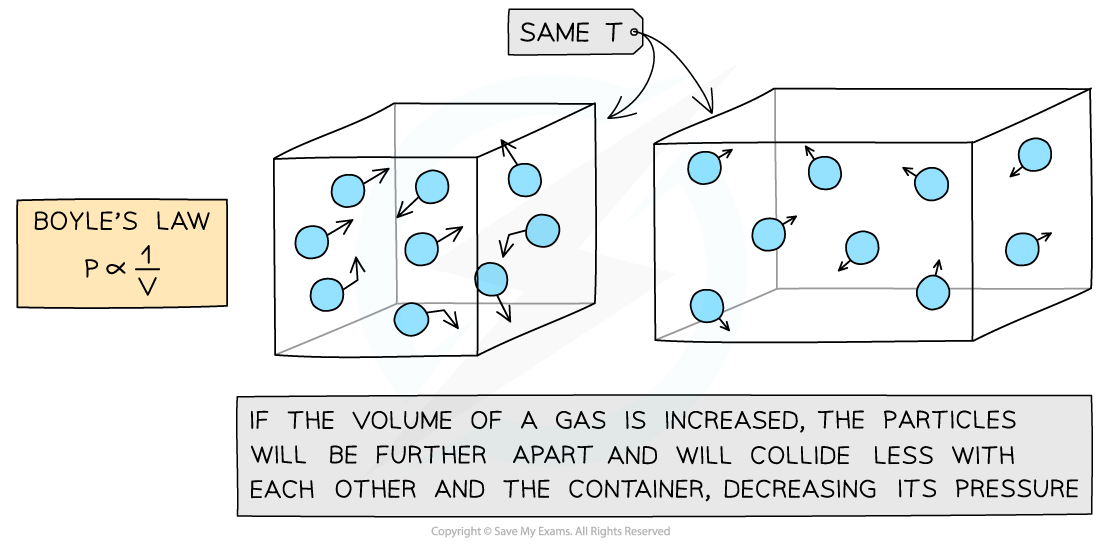
Diagram illustrating Boyle's Law with two boxes of gas particles, showing increased volume leads to reduced pressure due to fewer collisions.
Increasing the volume of a gas decreases its pressure

  • When the volume of the container is increased, the pressure decreases

    • The gas is expanded

    • The space in between the particles increases

    • The particles collide with the surfaces of the container less frequently

    • Resulting in a decrease in pressure

  • When the volume of the container is decreased, the pressure increases

    • The gas is compressed

    • The space in between the particles decreases

    • The particles collide with the surfaces of the container more frequently

    • Resulting in an increase in pressure

  • The  p V space equals space constant relationship can also be written as:

p subscript 1 V subscript 1 space equals space p subscript 2 V subscript 2

  • Where:

    • p1  = initial pressure in pascals (Pa)

    • V1  = initial volume in metres cubed (m3)

    • p2  = final pressure in pascals (Pa)

    • V2  = final volume in metres cubed (m3)

  • This relationship is often referred to as Boyle's Law

  • It is used to compare the pressure and volume before and after a change

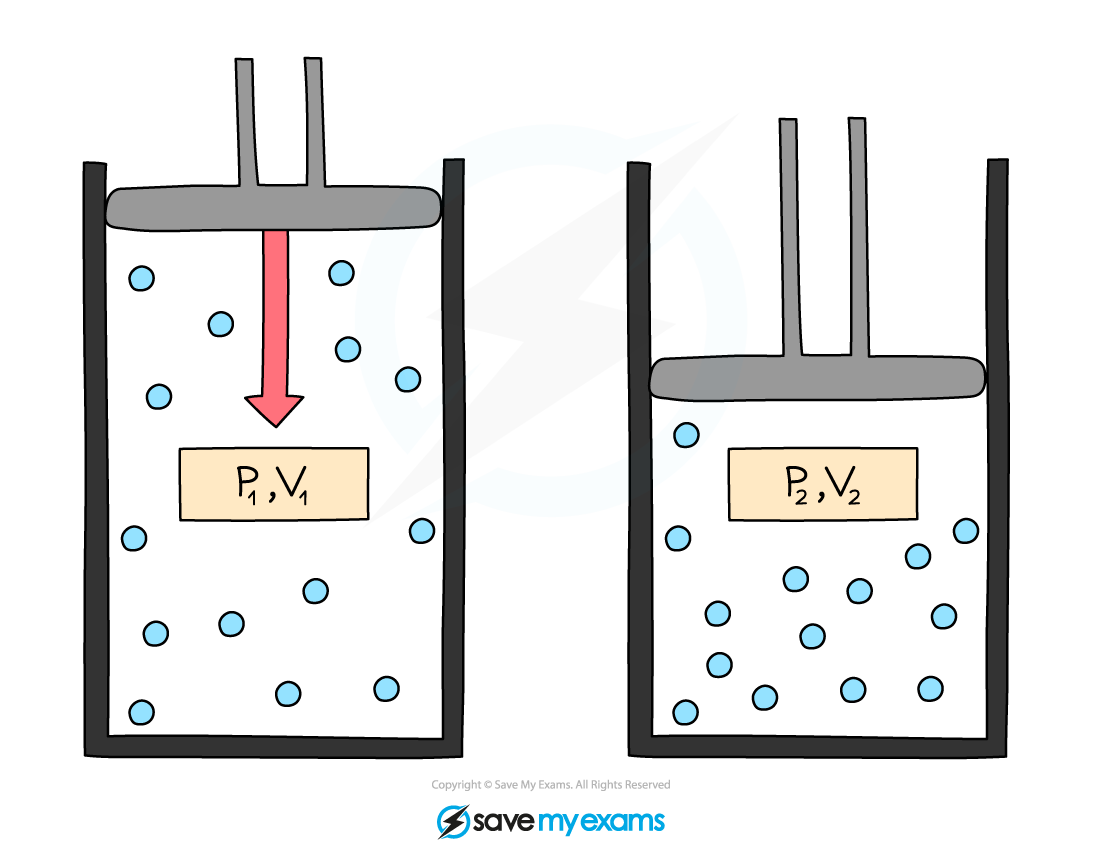
Two piston-cylinder diagrams comparing initial and final states. Left shows P1, V1 with a descending piston; right shows P2, V2 with a lower piston.
The initial pressure and volume are the values before the change, and the final pressure and volume are the values after the change

Worked Example

A gas occupies a volume of 0.70 m3 at a pressure of 203 Pa.

Calculate the pressure exerted by the gas after it has been compressed to a volume of 0.15 m3.

Assume that the temperature and mass of the gas stay the same. 

Answer:

Step 1: List the known variables

  • Initial pressure, p1 = 203 Pa

  • Initial volume, V1 = 0.70 m3 

  • Final volume, V2 = 0.15 m3 

Step 2: Write out the relationship

p subscript 1 V subscript 1 space equals space p subscript 2 V subscript 2

Step 3: Rearrange the relationship to make p2 the subject

  • Divide both sides by V2

fraction numerator p subscript 1 V subscript 1 over denominator V subscript 2 end fraction space equals space fraction numerator p subscript 2 down diagonal strike V subscript 2 end strike over denominator down diagonal strike V subscript 2 end strike end fraction

p subscript 2 space equals space fraction numerator p subscript 1 V subscript 1 over denominator V subscript 2 end fraction

Step 4: Substitute in the known values to calculate

p subscript 2 space equals space fraction numerator 203 space cross times space 0.70 over denominator 0.15 end fraction

p subscript 2 space equals space 947.3

Step 5: Round to an appropriate number of significant figures

  • The least precise input value is 2 s.f.

  • Therefore, the answer can only be given to the same precision

p subscript 2 space equals space 950 space Pa space open parentheses 2 space straight s. straight f. close parentheses

Examiner Tips and Tricks

Always check whether your final answer makes sense.

If the gas has been compressed, the final pressure is expected to be more than the initial pressure. If this is not the case, double-check the rearranging of any relationships and the values put into your calculator.

One pascal is a very small amount of pressure, and you will typically meet pressures in the order of kilo-pascals.

The pressure exerted on you right now due to air pressure is equal to 100 kPa, so use this as a reference when considering if your answer makes sense.

Pressure & temperature

  • Pressure is directly proportional to temperature

p space proportional to space T

  • Where:

    • p = pressure in pascals (Pa)

    • T = temperature in Kelvin (K)

  • This means that:

p over T space equals space constant

  • The pressure-temperature relationship only works when:

    • the gas is at a constant volume

    • the mass of the gas does not change

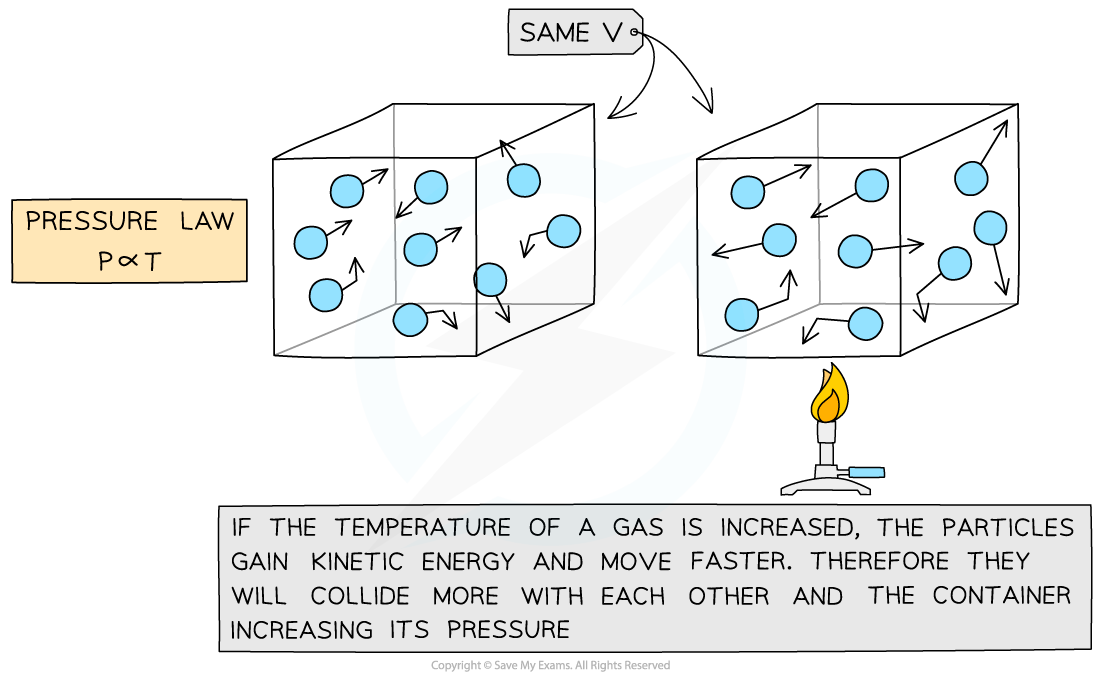
Diagram showing Pressure Law: P ∝ T with two containers. Heated gas molecules move faster, increasing pressure. Bunsen burner shown beneath one container.
An increase in temperature of the gas results in an increase in pressure for a fixed volume

  • When the temperature of the gas is increased, the pressure increases

    • The mean kinetic energy of the particles is increased

    • The particles travel faster

    • The particles collide with the surfaces of the container more frequently

    • The force of each collision increases

    • Resulting in an increase in pressure

  • When the temperature of the gas is decreased, the pressure decreases

    • The mean kinetic energy of the particles is decreased

    • The particles travel more slowly

    • The particles collide with the surfaces of the container less frequently

    • The force of each collision decreases

    • Resulting in a decrease in pressure

  • This relationship can also be written as:

p subscript 1 over T subscript 1 space equals fraction numerator space p subscript 2 over denominator T subscript 2 end fraction

  • Where:

    • P1 = initial pressure (Pa)

    • P2 = final pressure (Pa)

    • T1 = initial temperature (K)

    • T2 = final temperature (K)

  • This relationship is sometimes referred to as the pressure law or Gay-Lussac's law

  • It can be used to compare the pressure and temperature before and after a change

Worked Example

The pressure inside a bicycle tyre is 5.10 × 105 Pa when the temperature is 279 K. After the bicycle has been ridden, the temperature of the air in the tyre is 299 K.

Calculate the new pressure in the tyre, assuming the volume is unchanged.

Answer:

Step 1: List the known quantities

  • Initial pressure, p subscript 1 space equals space 5.10 cross times 10 to the power of 5 space Pa

  • Initial temperature, T subscript 1 space equals space 279 space straight K

  • Final temperature, T subscript 2 space equals space 299 space straight K

Step 2: Write out the relevant relationship

p subscript 1 over T subscript 1 space equals fraction numerator space p subscript 2 over denominator T subscript 2 end fraction

Step 3: Rearrange to make p subscript 2 the subject

  • Multiply both sides by T subscript 2

T subscript 2 p subscript 1 over T subscript 1 space equals fraction numerator space p subscript 2 over denominator up diagonal strike T subscript 2 end strike end fraction up diagonal strike T subscript 2 end strike

p subscript 2 space equals space fraction numerator p subscript 1 T subscript 2 over denominator T subscript 1 end fraction

Step 4: Substitute in the known values to calculate

p subscript 2 space equals space fraction numerator open parentheses 5.10 cross times 10 to the power of 5 close parentheses space cross times space 299 over denominator 279 end fraction

p subscript 2 space equals space 5.4656 cross times 10 to the power of 5 space Pa

Step 5: Round to an appropriate amount of significant figures

  • The least precise input value is 3 s.f.

  • Therefore, the answer can only be given to this level of precision

p subscript 2 space equals space 5.47 cross times 10 to the power of 5 space Pa space open parentheses 3 space straight s. straight f. close parentheses

Volume & temperature

  • Volume is directly proportional to temperature

V space proportional to space T

  • Where:

    • V = volume in metres cubed (m3)

    • T = temperature in Kelvin (K)

  • This means that:

V over T space equals space constant

  • The volume-temperature relationship only works when:

    • the gas is at a constant pressure

    • the mass of the gas does not change

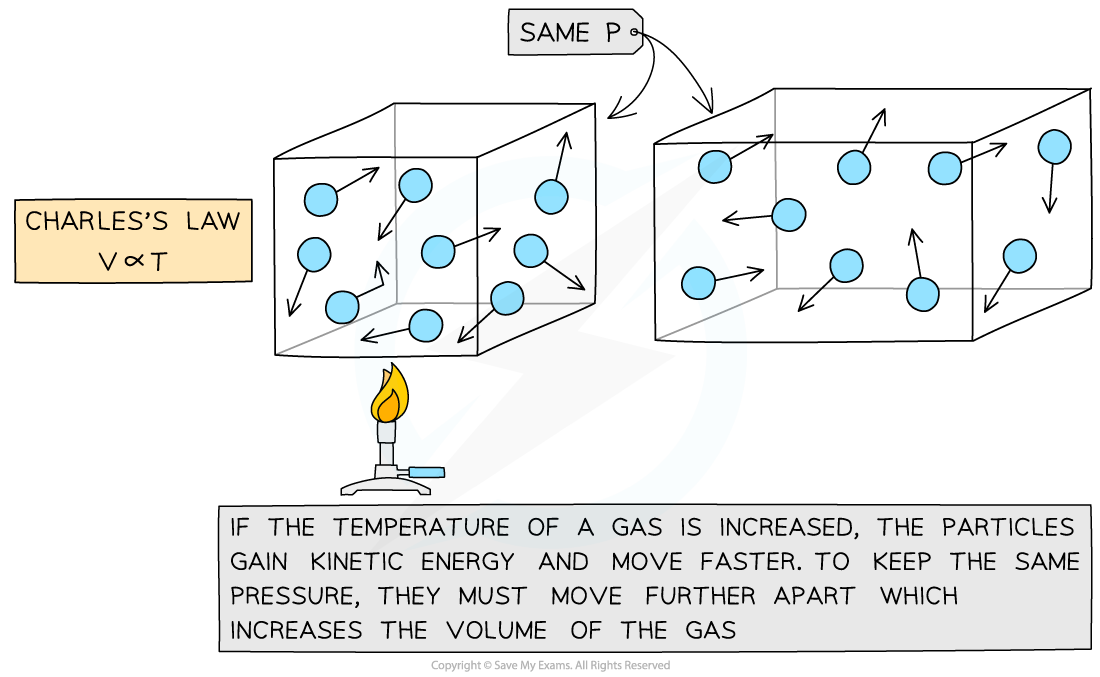
Diagram explaining Charles's Law: as gas temperature rises, particles move faster, forcing them apart and increasing volume while maintaining pressure.
If the temperature of the gas is increased, the volume of the gas will increase, for a fixed pressure

  • When the temperature of the gas is increased, the volume increases

    • The mean kinetic energy of the particles is increased

    • The particles travel faster

    • The space in between the particles increases

    • Resulting in an increase in volume

  • When the temperature of the gas is decreased, the volume decreases

    • The mean kinetic energy of the particles is decreased

    • The particles travel more slowly

    • The space in between the particles decreases

    • Resulting in a decrease in volume

  • This relationship can also be written as:

V subscript 1 over T subscript 1 space equals fraction numerator space V subscript 2 over denominator T subscript 2 end fraction

  • Where:

    • V1 = initial volume (m3)

    • V2 = final volume (m3)

    • T1 = initial temperature (K)

    • T2 = final temperature (K)

  • This relationship is often referred to as Charles' Law

  • It is used to compare the volume and temperature before and after a change

Examiner Tips and Tricks

Note that all temperature values must be in Kelvin for the gas law calculations. If temperatures are given in °C, then you must convert them to Kelvin. See the revision note Absolute Zero for a reminder on how to do this.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:The Kinetic ModelNext:Gas Law Experiments
    Author
    Reviewer
    Leander Oates

    Author: Leander Oates

    Expertise: Physics Content Creator

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.

    Caroline Carroll

    Reviewer: Caroline Carroll

    Expertise: Physics & Chemistry Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.