IBMathsDPAnalysis & Approaches (AA)HLRevision Notes1. Number & AlgebraExponentials & LogsLaws of Logarithms

Laws of Logarithms (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Written by: Amber

Reviewed by: Mark Curtis

Updated on

DP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): SL

Did this video help you?

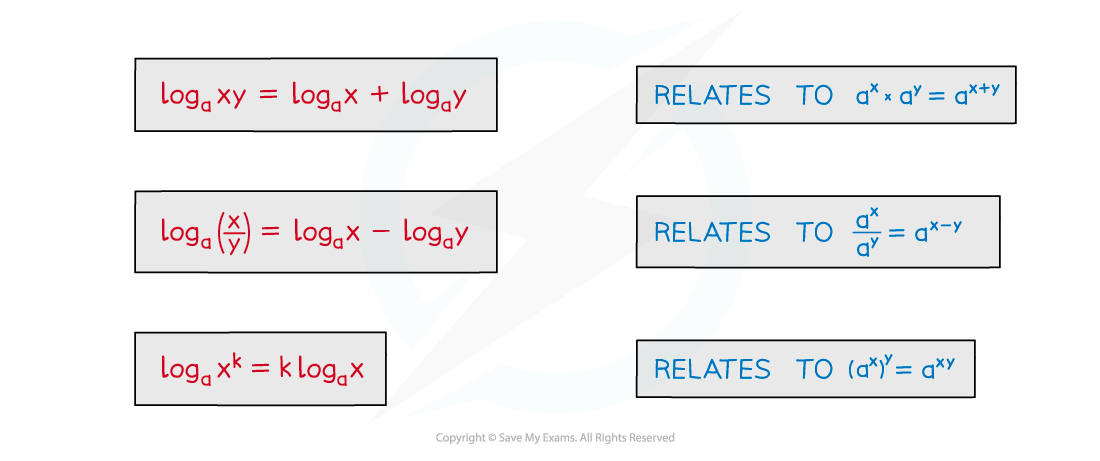
Laws of Logarithms

What are the laws of logarithms?

  • The laws of logarithms (log laws) you need to know are:

    • log subscript a x y equals blank log subscript a x plus blank log subscript a y

    • log subscript a x over y equals blank log subscript a x blank negative space log subscript a y

    • log subscript a x to the power of m equals blank m log subscript a x

  • These hold for a comma space x comma space y greater than 0

Examiner Tips and Tricks

The laws of logarithms are given in the formula booklet.

Logarithmic laws and their equivalent exponential forms, showing relationships between multiplication, division, and powers in logarithms and exponents.

Useful results from the laws of logarithms

  • log subscript a 1 equals 0

    • This is equivalent to a to the power of 0 equals 1

  • log subscript a a equals 1

    • This is equivalent to a to the power of 1 equals a

  • log subscript a a to the power of k equals blank k

    • because log subscript a a to the power of k equals blank k log subscript a a equals k cross times 1

  • a to the power of log subscript a x end exponent equals blank x

    • because logarithms and powers are inverses

  • log subscript a 1 over x equals negative log subscript a x

    • because log subscript a 1 over x equals log subscript a 1 minus log subscript a x equals 0 minus log subscript a x

Examiner Tips and Tricks

These useful results from log laws are not in the formula booklet.

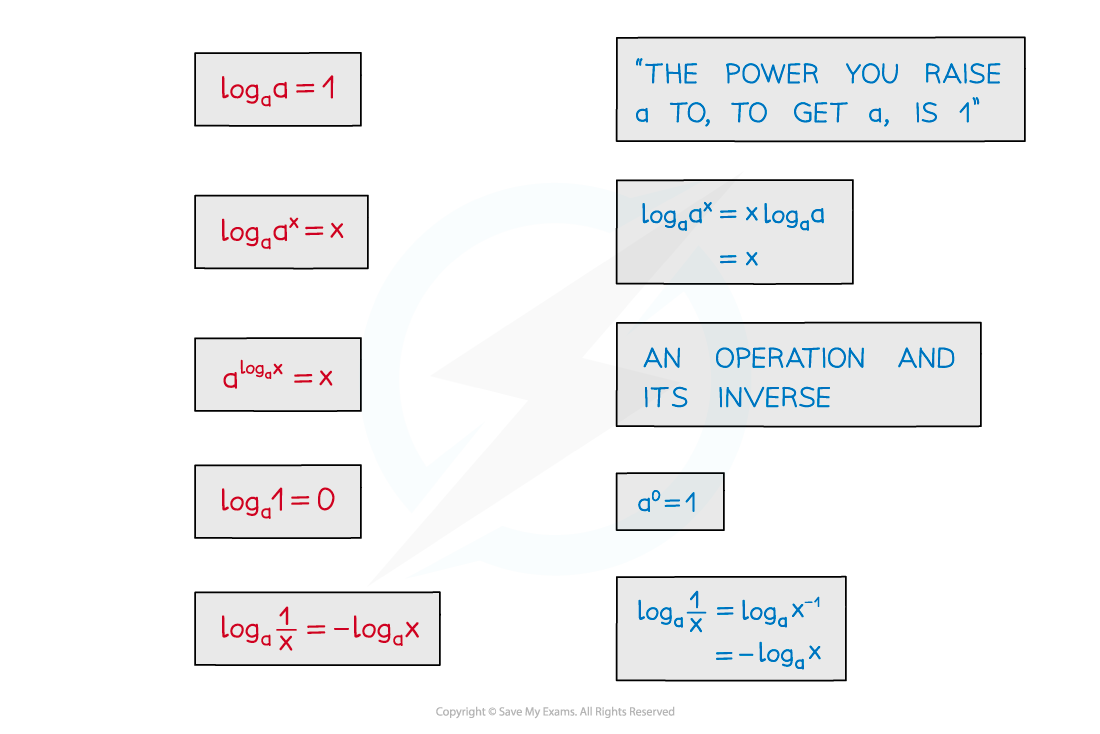
Mathematical properties of logarithms and exponents with examples, including inverse relationships and expressions for logs and powers.

  • The useful results can be applied to ln space x space left parenthesis log subscript e x right parenthesis too

    • Two particularly useful results are

      • ln space straight e to the power of x space equals space x

      • straight e to the power of ln x end exponent space equals space x

Examiner Tips and Tricks

Beware: log subscript a open parentheses x plus y close parentheses not equal to log subscript a x plus log subscript a y

When are logarithms undefined?

  • You cannot take the log of zero or the log of a negative number

    • log subscript a x is defined for x greater than 0

    • log subscript a x is undefined for x less or equal than 0

  • Similarly

    • log subscript a open parentheses x minus 5 close parentheses is defined for x greater than 5

    • log subscript a open parentheses x minus 5 close parentheses is undefined for x less or equal than 5

    • etc

Examiner Tips and Tricks

When solving an equation involving logs, get rid of any solutions that make the original equation undefined.

Worked Example

a) Write the expression 2 log space 4 minus log space 2 in the form log space k, where k element of straight integer numbers.

 

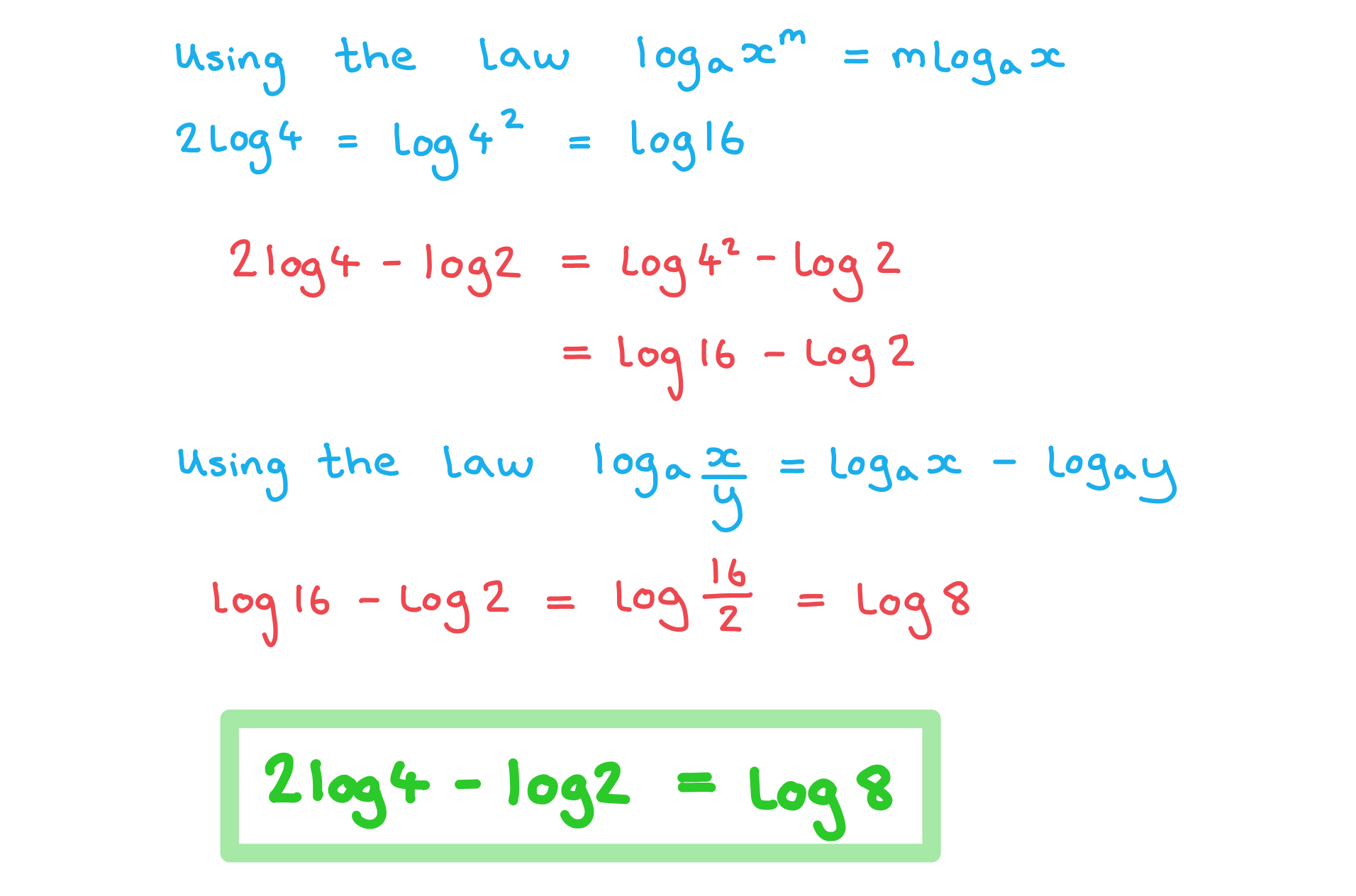
aa-sl-1-2-2-laws-of-logs-we-solution-part-a

b)   Hence, or otherwise, solve 2 log space 4 minus log space 2 equals negative log blank 1 over x.

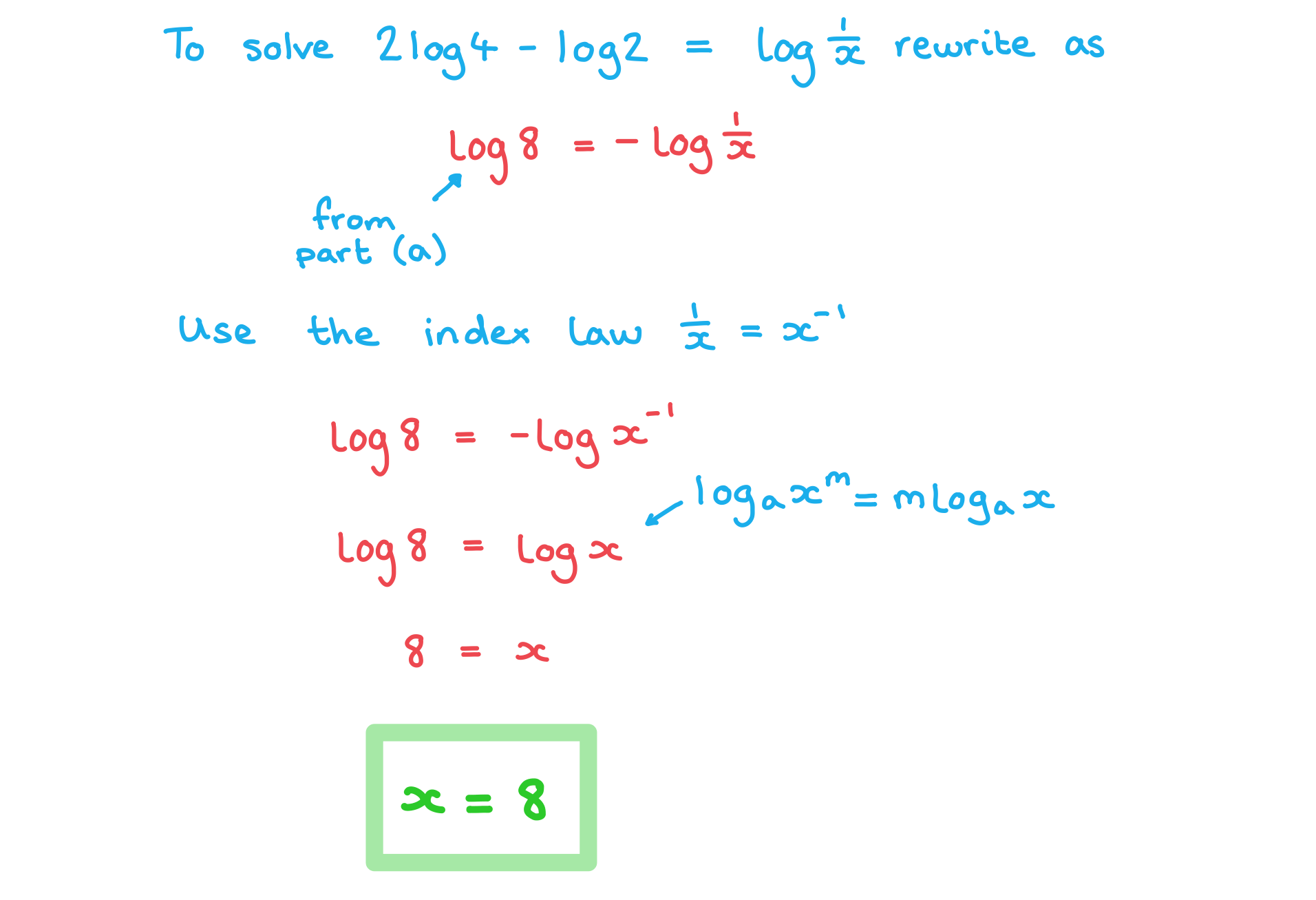
aa-sl-1-2-2-laws-of-logs-we-solution-part-b

Did this video help you?

Change of base

How do I change the base of a logarithm?

  • The formula for changing the base of a logarithm is

log subscript a x equals fraction numerator log subscript b x over denominator log subscript b a end fraction

  • This allows you to change logarithms into a more useful base

    • which is helpful in non-calculator questions

Examiner Tips and Tricks

The formula for changing the base of a logarithm is given in the formula booklet.

Worked Example

By choosing a suitable value for b, use log subscript a x equals fraction numerator log subscript b x over denominator log subscript b a end fraction to find the value of  log subscript 8 space end subscript 32 without using a calculator.

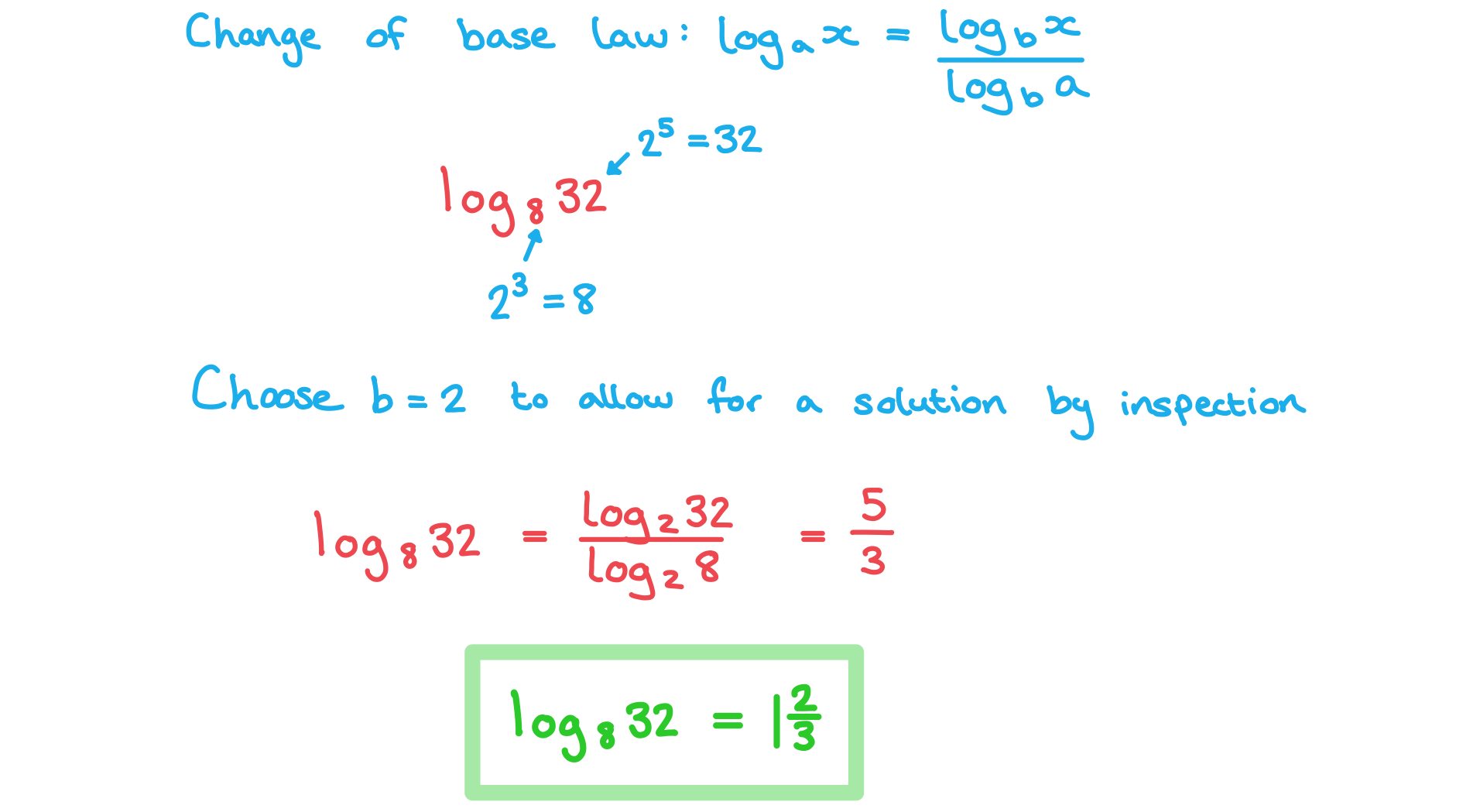
aa-sl-1-2-2-change-of-base-we-solution-1

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourselfFlashcards

Did this page help you?

Previous:Introduction to LogarithmsNext:Solving Exponential Equations
Author
Reviewer
Amber

Author: Amber

Expertise: Maths Content Creator

Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

Mark Curtis

Reviewer: Mark Curtis

Expertise: Maths Content Creator

Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

Download notes on Laws of Logarithms