Reciprocal Transformations (DP IB Analysis & Approaches (AA)): Revision Note
Reciprocal transformations
What effects do reciprocal transformations have on the graphs?
The x-coordinates stay the same
The y-coordinates change
Their values become their reciprocals
The coordinates (x, y) become
where y ≠ 0
If y = 0 then a vertical asymptote goes through the original coordinate
Points that lie on the line y = 1 or the line y = -1 stay the same
How do I sketch the graph of the reciprocal of a function: y = 1/f(x)?
Sketch the reciprocal transformation by considering the different features of the original graph
Consider key points on the original graph
If (x1, y1) is a point on y = f(x) where y1 ≠ 0
is a point on
If |y1| < 1 then the point gets further away from the x-axis
If |y1| > 1 then the point gets closer to the x-axis
If y = f(x) has a y-intercept at (0, c) where c ≠ 0
The reciprocal graph
has a y-intercept at
If y = f(x) has a root at (a, 0)
The reciprocal graph
has a vertical asymptote at
If y = f(x) has a vertical asymptote at
The reciprocal graph
has a discontinuity at (a, 0)
The discontinuity will look like a root
If y = f(x) has a local maximum at (x1, y1) where y1 ≠ 0
The reciprocal graph
has a local minimum at
If y = f(x) has a local minimum at (x1, y1) where y1 ≠ 0
The reciprocal graph
has a local maximum at
Consider key regions on the original graph
If y = f(x) is positive then
is positive
If y = f(x) is negative then
is negative
If y = f(x) is increasing then
is decreasing
If y = f(x) is decreasing then
is increasing
If y = f(x) has a horizontal asymptote at y = k
has a horizontal asymptote at
if k ≠ 0
tends to ± ∞ if k = 0
If y = f(x) tends to ± ∞ as x tends to +∞ or -∞
has a horizontal asymptote at
Worked Example
The diagram below shows the graph of which has a local maximum at the point A.
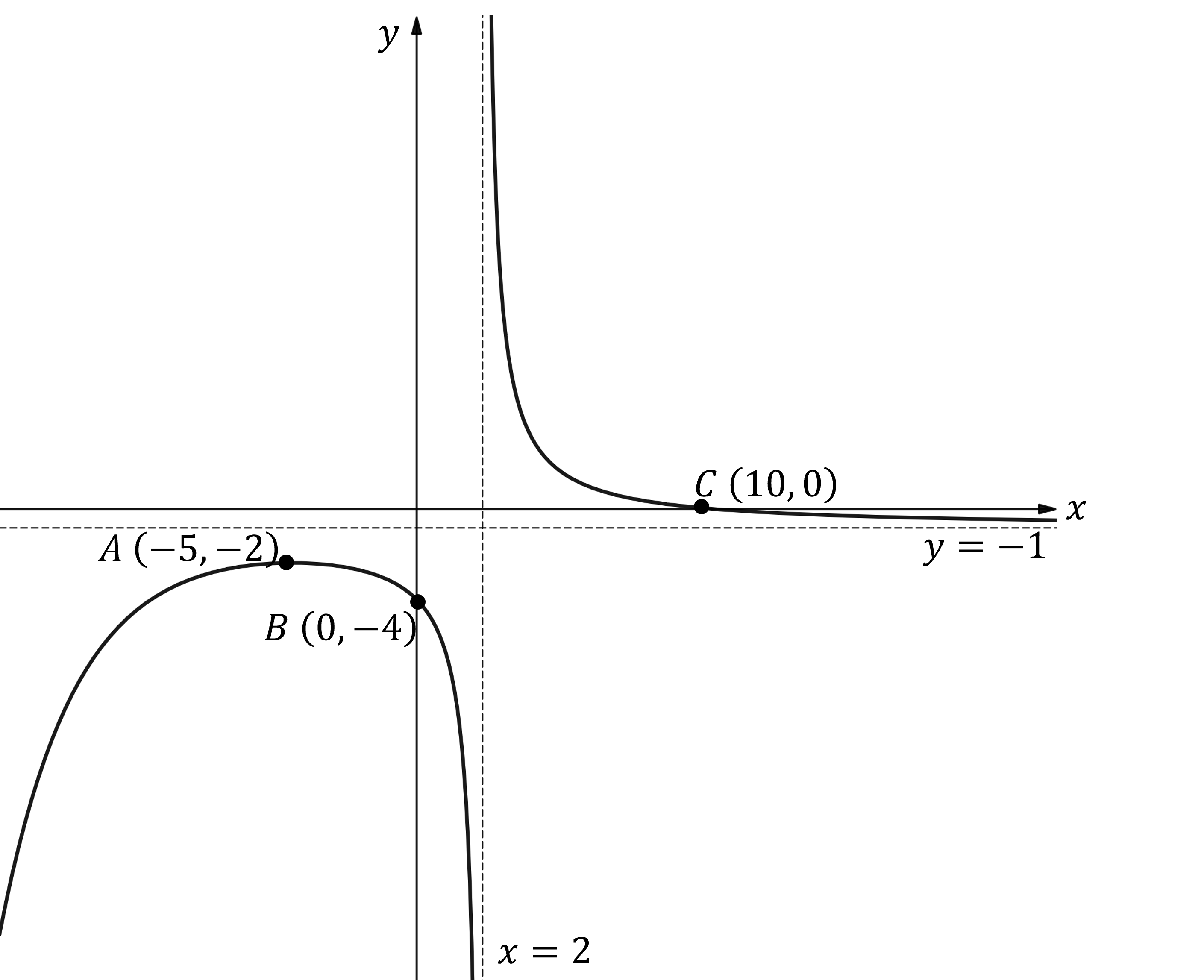
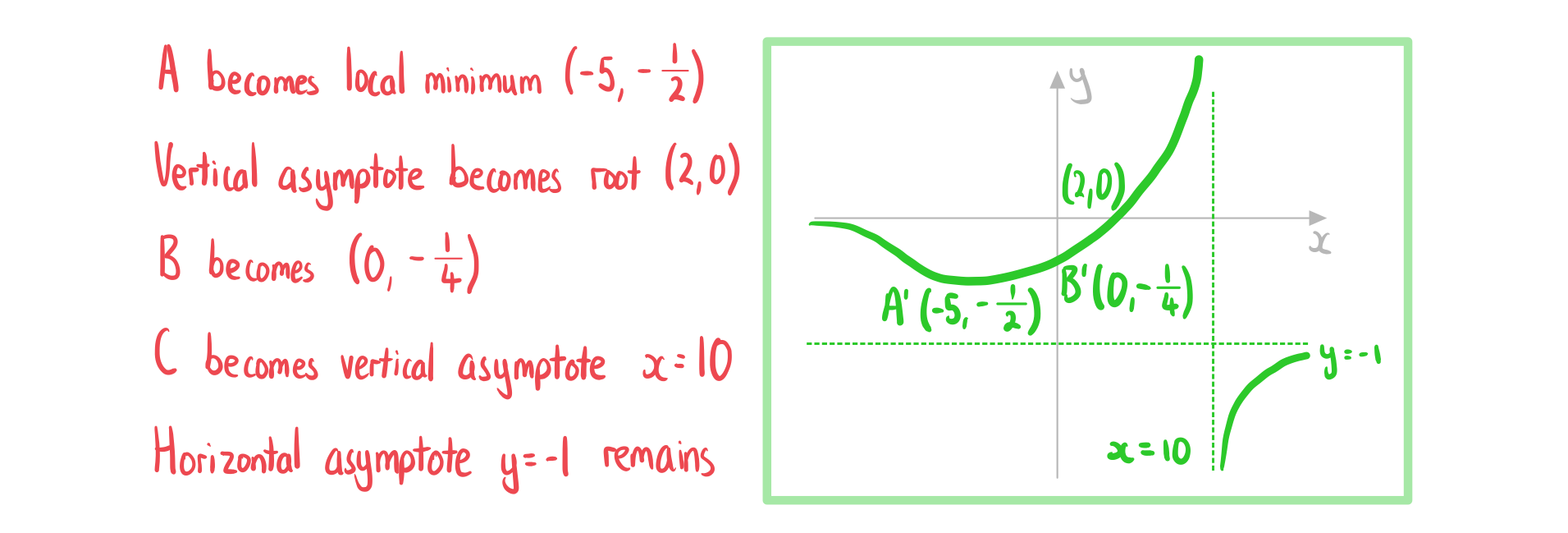
Sketch the graph of ..

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?