National 5PhysicsSQARevision NotesDynamicsVectors & ScalarsCalculations with Vectors

Calculations with Vectors (SQA National 5 Physics): Revision Note

Exam code: X857 75

Katie M

Written by: Katie M

Reviewed by: Leander Oates

Updated on

Calculations with vectors

  • Two vectors can be combined to produce a resultant vector

  • The resultant vector describes the combined effect of both vectors

  • Vectors may be

    • in one dimension (along a straight line)

    • at right angles to each other

Combining vectors on a straight line

  • Vectors acting along the same line are added or subtracted

    • Vectors acting in the same direction are added together

    • Vectors acting in opposite directions are subtracted from each other

  • For two vectors act in opposite directions:

    • if they have equal magnitudes, the resultant vector will be zero

    • if they have unequal magnitudes, the resultant vector will act in the same direction as the vector with the larger magnitude

  • Consider a man walking along a travelator (conveyor belt)

    • The travelator is moving at a constant velocity of 1 m s-1 to the right

    • The man is walking at a constant speed of 2 m s-1

  • The magnitude of the man's velocity depends on the direction he walks along the travelator

  • If he walks in the same direction as the travelator's movement, i.e. at a velocity of 2 m s-1 to the right, then his velocity will be:

Resultant space velocity space equals space 2 space plus space 1 space equals space 3 space straight m space straight s to the power of negative 1 end exponent to the right

  • If he walks in the opposite direction to the travelator's movement, i.e. at a velocity of 2 m s-1 to the left, then his velocity will be:

Resultant space velocity space equals space 2 space plus space open parentheses negative 1 close parentheses space equals space 1 space straight m space straight s to the power of negative 1 end exponent to the left

Resultant velocity of a man on a travelator

A man walking at a speed of 2 metres per second on a conveyor belt moving at 1 metre per second. Left diagram: Resultant velocity = 3 metres per second to the right when walking with the belt. Right diagram: Resultant velocity = 1 metre per second to the left when walking against the belt.
When the two velocities are in the same direction, they are added together. When the two velocities are in opposite directions, one is subtracted from the other

Combining vectors at right angles

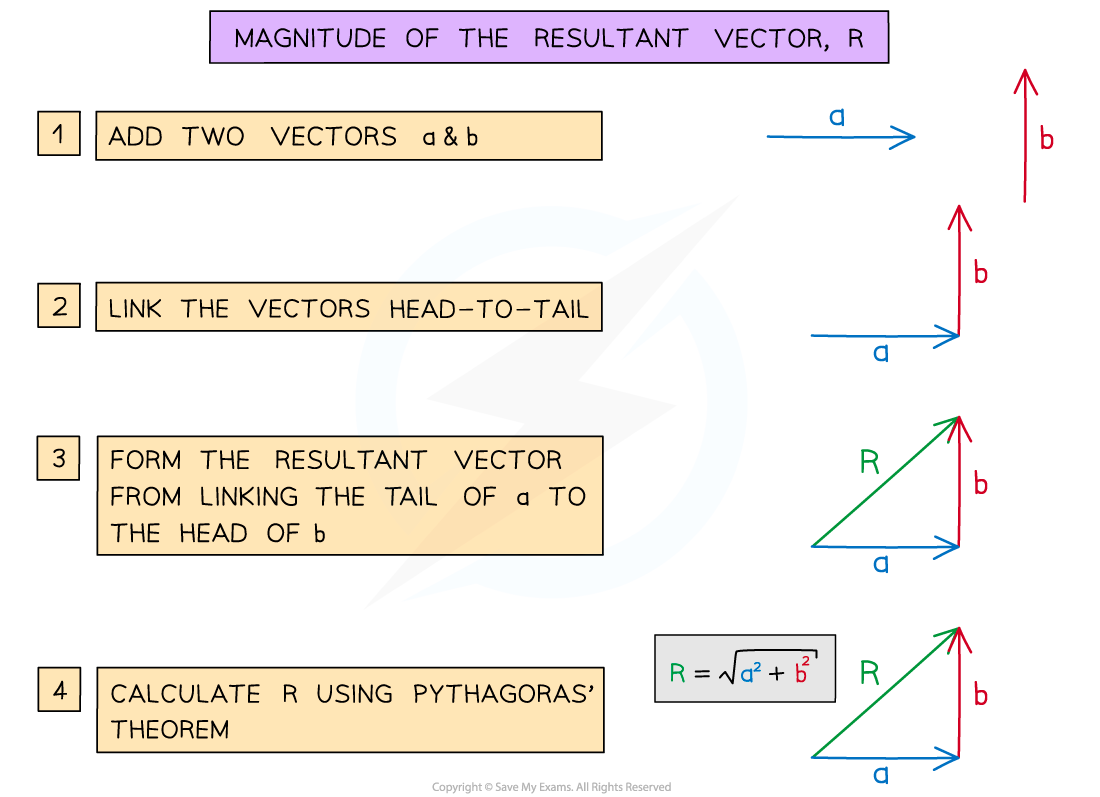
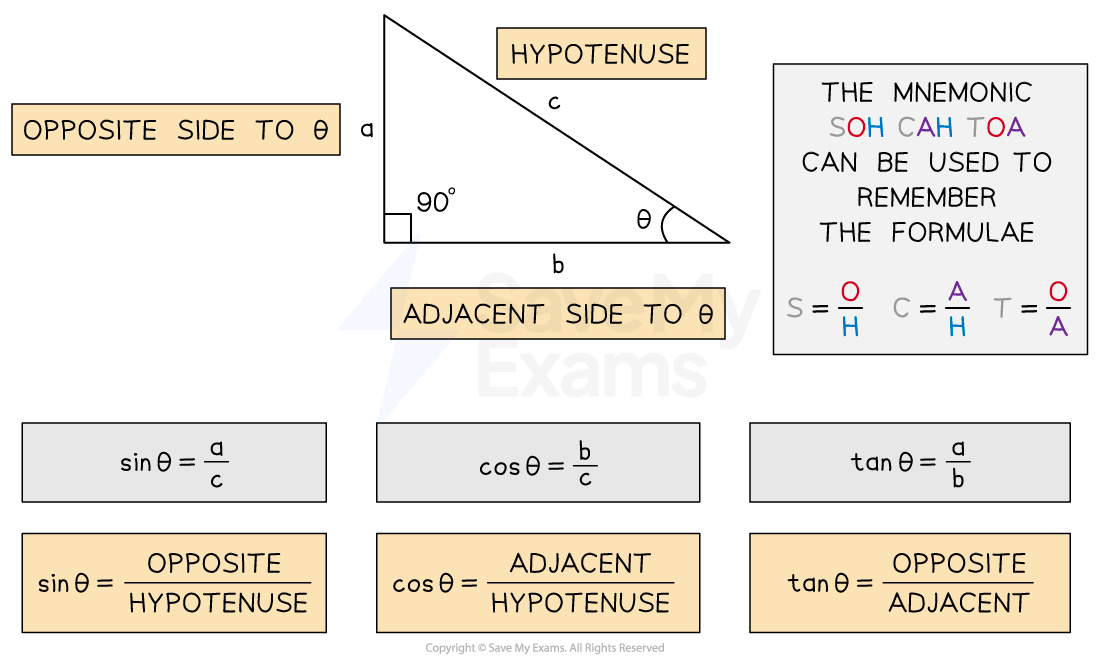
Finding the magnitude of the vector

  • The magnitude of the resultant vector can be found using Pythagoras' theorem

c squared space equals space a squared space plus space b squared

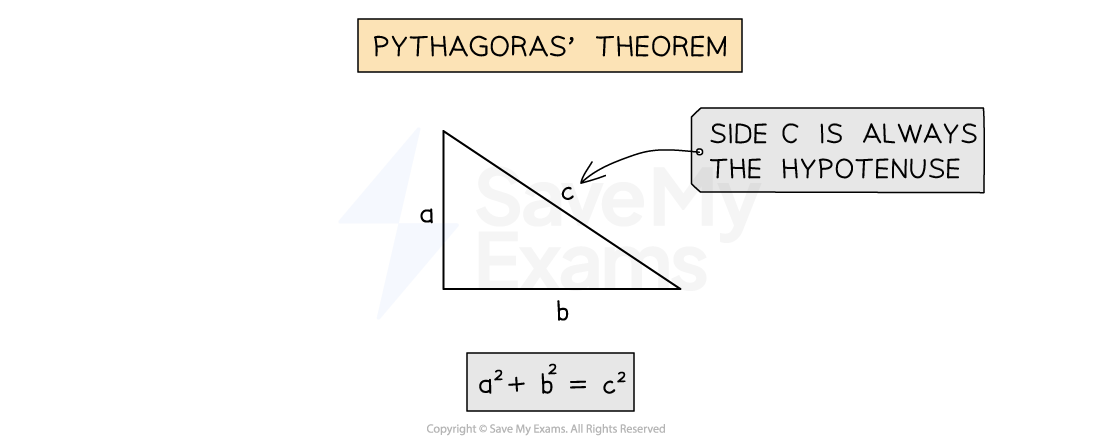
A right-angled triangle labeled with sides 'a', 'b', and hypotenuse 'c' and a note saying 'Side c is always the hypotenuse'. Below is the equation a^2 + b^2 = c^2.
Pythagoras' theorem is used to find the length of an unknown side of a right angled triangle

  • For two vectors, a and b, acting at right angles, the resultant vector R is the hypotenuse of the triangle

R squared space equals space a squared space plus space b squared

R space equals space square root of a squared space plus space b squared end root

  • Note: The vectors must always be drawn head-to-tail

Steps to find the magnitude of resultant vector R using vectors a and b. Diagram illustrates vector addition and Pythagoras’ theorem.
The magnitude of the resultant vector is found by using Pythagoras’ theorem

Finding the direction of the vector

  • The direction of the resultant vector can be found using trigonometry

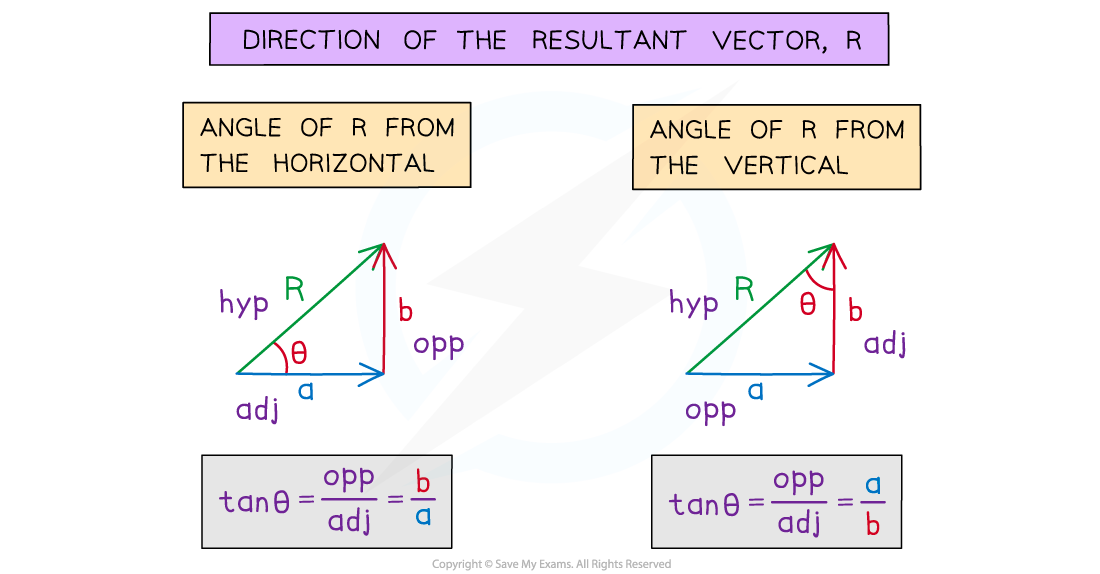
Two right-angled triangles where resultant vector R is the hypotenuse and vector a is the horizontal edge, and vector b is the vertical edge. Left triangle: angle between R and the horizontal, in this case, tan(θ) = b/a. Right triangle: angle between R and the vertical, in this case, tan(θ) = a/b.
The ratio of the vectors depends on where the angle is in the triangle

  • For two vectors, a and b, acting at right angles, where a is opposite to the angle and b is adjacent, use the inverse tan function to find the angle

tan space theta space equals space opposite over adjacent space equals space a over b

theta space equals space tan to the power of negative 1 end exponent space open parentheses a over b close parentheses

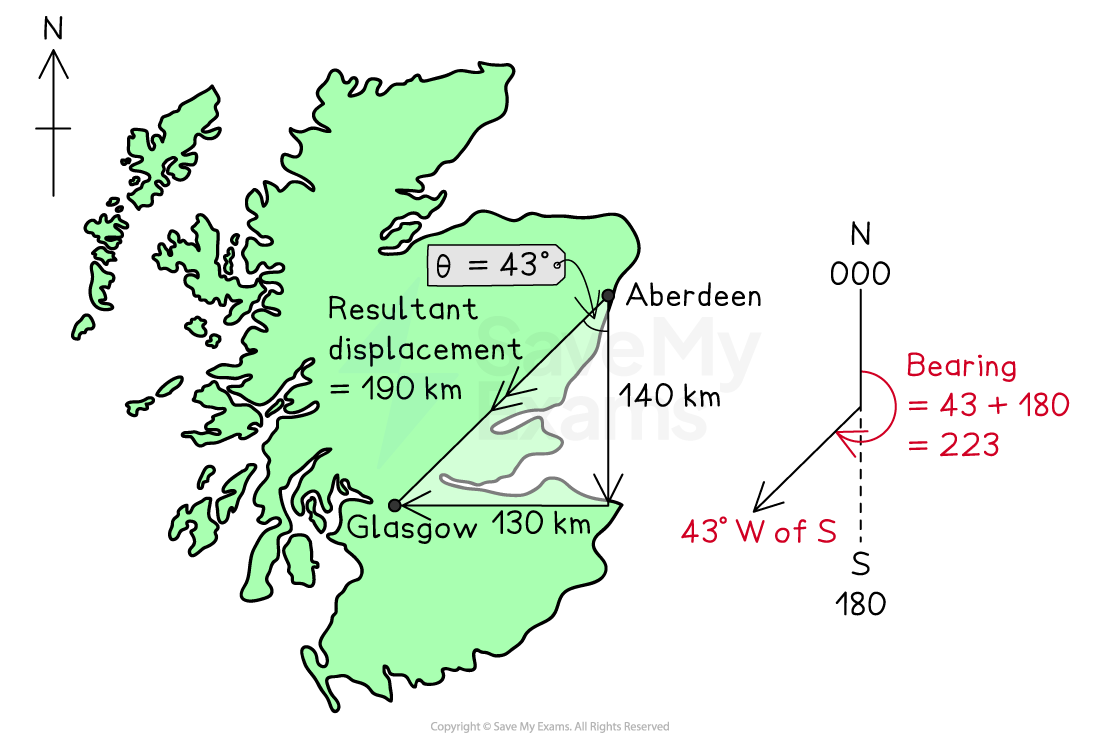
  • If a plane flies 140 km south from Aberdeen, and then 130 km west to Glasgow, the magnitude of the displacement is:

s space equals space square root of 140 squared space plus space 130 squared end root space equals space 190 space km

  • The direction of the displacement from Aberdeen to Glasgow is:

tan space theta space equals space opposite over adjacent space equals space 130 over 140

theta space equals space 43 degree space straight W space of space straight S, or bearing space equals space 223

  • Therefore, the resultant displacement is 190 km on a bearing of 223 (or 43° west of south)

Map of Scotland showing vector displacement from Aberdeen to Glasgow. Arrows show 140 km south and 130 km west, with a 43° angle and a resultant 190 km vector.
The resultant displacement is the shortest distance from Aberdeen to Glasgow and is marked with a double arrow. The magnitude can be worked out using Pythagoras theorem and the direction can be worked out using trigonometry. The direction should be given relative to the compass, or as a bearing.

Examiner Tips and Tricks

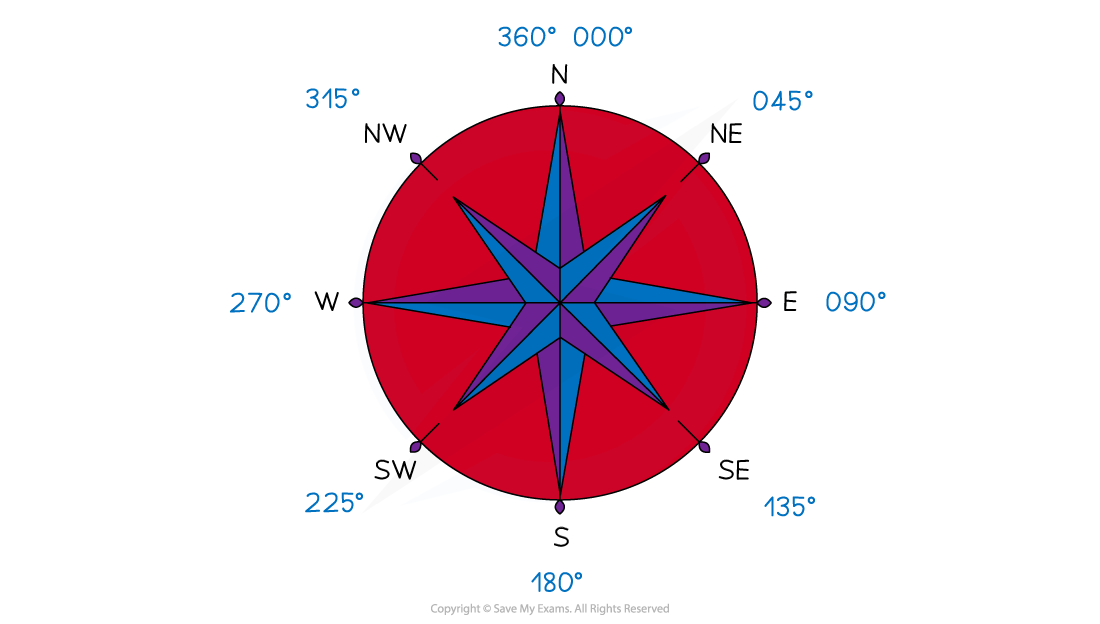
When a question includes compass points or bearings, this gives you a point of reference between your start point and end point, so you must give the direction of any vector relative to a point on a compass or as a bearing.

When using a bearing, follow these three rules:

  • They are measured from due North

    • North is usually straight up on a scale drawing or map, and should be labelled on the diagram

  • They are measured clockwise

  • The angle should always be written with 3 digits, and the degree symbol is not needed

    • 059 instead of just 59°

Therefore, you should practice compass directions and their respective bearings if you are not confident with these

Compass direction bearings

Worked Example

A boat travels across a river that is flowing due east at a speed of 1.5 m s-1. The boat starts from the north bank of the river and moves at a constant speed of 3.5 m s-1 towards the south bank.

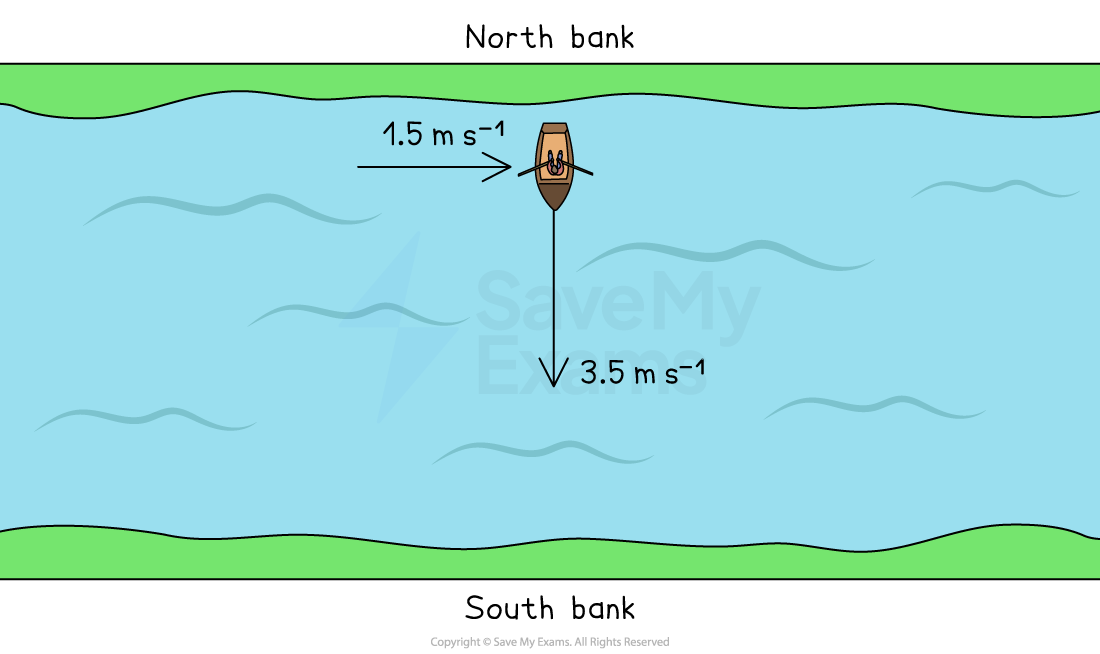
A boat on a river travels at 3.5 metres per second from the north bank to the south bank. An arrow indicates the river flows east at 1.5 metres per second.

Determine the magnitude and direction of the boat's resultant velocity.

Answer:

Step 1: Draw a vector triangle to identify the resultant vector and its direction

  • The vectors should be drawn tip-to-tail

  • The resultant R is drawn from the start of the first vector to the end of the second

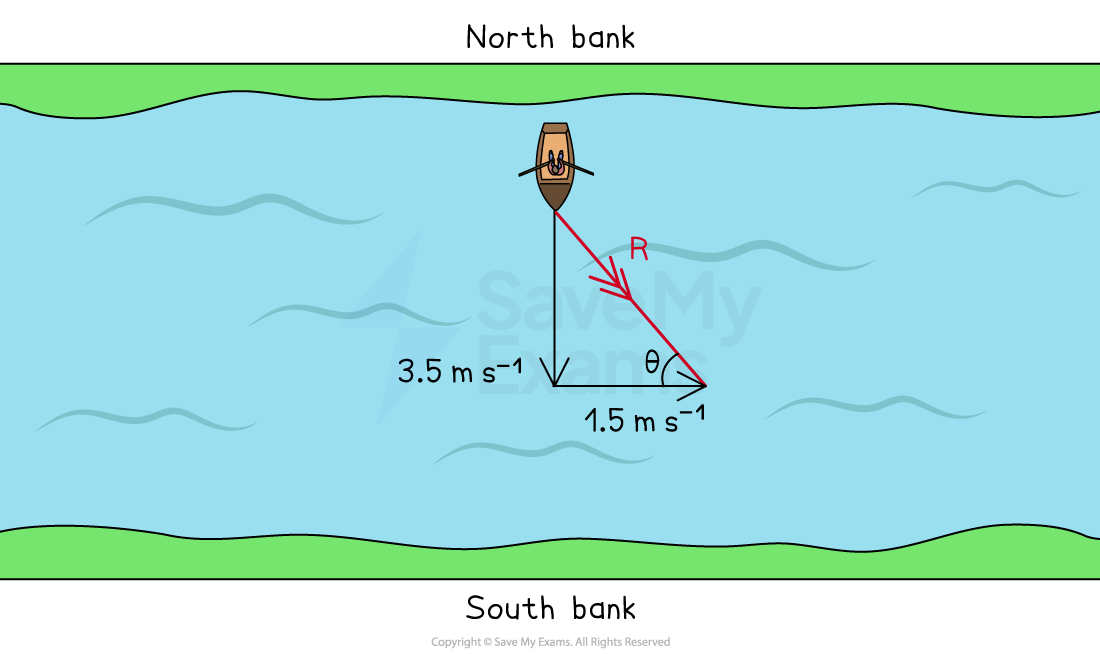
Boat moving on water between north and south banks, with vectors showing speeds of 3.5 m/s north and 1.5 m/s east, forming angle θ with resultant R.

Step 2: Calculate the magnitude of the resultant using Pythagoras' theorem

R squared space equals space a squared space plus space b squared space equals space 3.5 squared space plus space 1.5 squared 

R space equals space square root of 3.5 squared space plus space 1.5 squared end root

R space equals space 3.8 space straight m space straight s to the power of negative 1 end exponent

Step 3: Calculate the direction of the resultant using trigonometry

 tan space theta space equals space opposite over adjacent

tan space theta space equals space fraction numerator 3.5 over denominator 1.5 end fraction

theta space equals space tan to the power of negative 1 end exponent space open parentheses fraction numerator 3.5 over denominator 1.5 end fraction close parentheses space equals space 67 degree

Step 4: State the final answer, complete with magnitude and direction

  • Since the question is given in terms of compass points, the direction can be given as

    • a bearing of 67 space plus thin space 90 space equals space 157

    • 67 degree south of east

    • 23 degree east of south

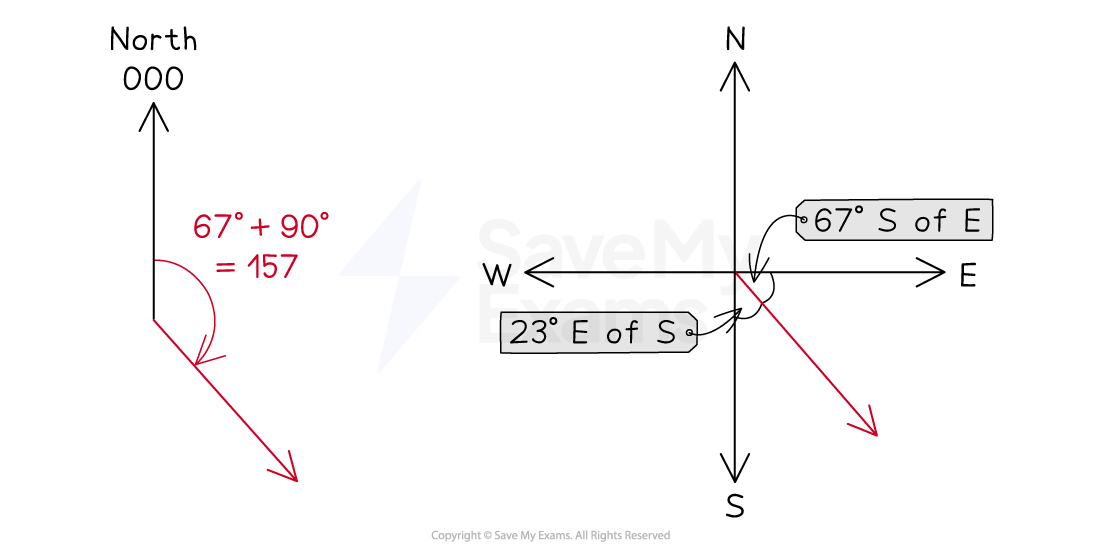
A compass rose with arrows indicating 67 degrees south of east and 23 degrees east of south, with calculations for a bearing of 157 degrees.

  • Therefore, the boat's resultant velocity is 3.8 space straight m space straight s to the power of negative 1 end exponent on a bearing of 157

Examiner Tips and Tricks

If the question specifically asks you to use the calculation or scale diagram, you must solve the problem as asked. However, if the choice is left up to you, then either method will lead to the correct answer.

Using scale diagrams sometimes feels easier than calculating, but once you are confident with using Pythagoras' theorem and trigonometry, you may find calculating a quicker and more accurate method.

This revision note covers how to calculate the angle using the tangent formula, but equally, the trigonometric ratios for sine or cosine could also be used, depending on which values you have.

Diagram of a right triangle with sides a, b, and hypotenuse c. Includes trigonometric ratios: sin θ = a/c, cos θ = b/c, tan θ = a/b, and mnemonic SOHCAHTOA.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Vector & Scalar QuantitiesNext:Scale Diagrams
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Leander Oates

    Reviewer: Leander Oates

    Expertise: Physics Content Creator

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.