Half-Life (SQA National 5 Physics): Revision Note

Half-life

• Half-life is defined as:

The time taken for the activity of a radioactive source to halve

• The activity is the number of nuclear disintegrations per unit time

• Since radioactive decay is a random process, it is impossible to know when any particular unstable nucleus will decay

• However, the decrease in activity can be measured and predicted

• Activity decreases with time because the number of unstable nucleii gradually decreases

• This leaves fewer and fewer unstable nuclei available to decay and emit radiation

• Different radioactive substances have different half-lives

• Half-lives can vary from a fraction of a second to billions of years in length

Measuring half-life

• To determine the half-life of a sample, the procedure is:

  • Measure the initial activity A₀ of the sample using a Geiger counter

  • Correct for back ground radiation

  • Determine the half-life of this original activity

  • Measure how the activity changes with time

• The time taken for the activity to decrease to half its original value is the half-life

Accounting for background radiation

• Background radiation must be accounted for when taking readings in a laboratory

• This can be done by taking readings with no radioactive source present and then subtracting this from readings with the source present

• This is known as the corrected count rate

Measuring background count rate

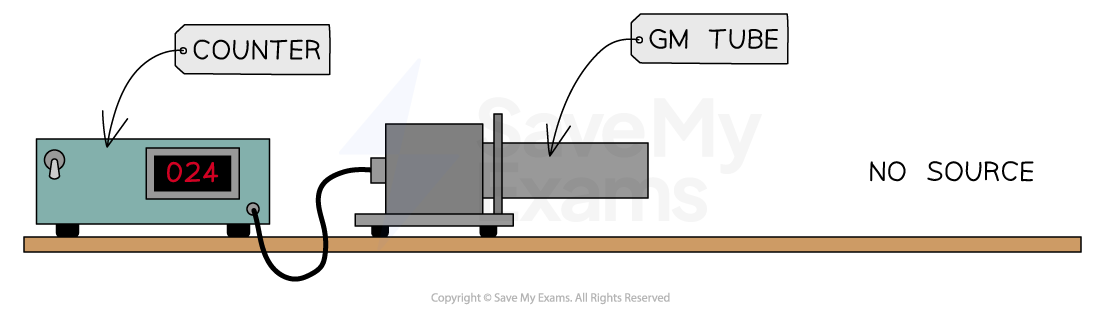
• For example, if a Geiger counter records 24 counts in 1 minute when no source is present, the background radiation count rate would be:

  • 24 counts per minute

  • 24/60 = 0.4 counts per second

Measuring the corrected count rate of a source

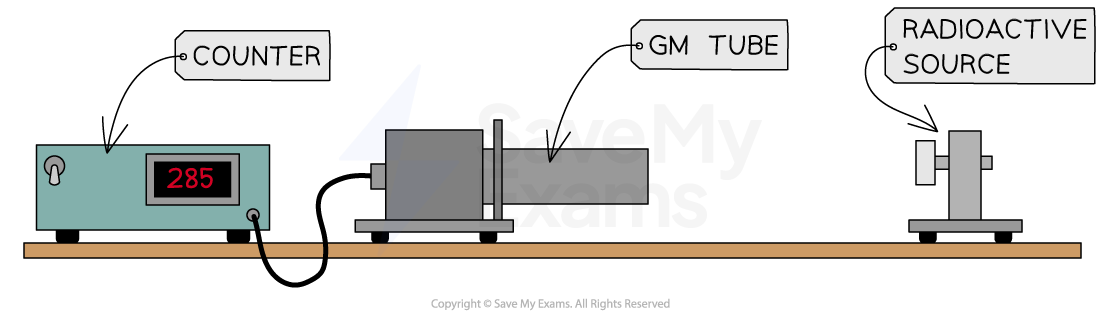
• Then, if the Geiger counter records, for example, 285 counts in 1 minute when a source is present, the corrected count rate would be:

  • 285 − 24 = 261 counts per minute

  • 261/60 = 4.35 counts per second

• When measuring count rates, the accuracy of results can be improved by:

  • Repeating readings and taking averages

  • Taking readings over a long period of time

Uses of half-life

• The half-life of a radioactive substance makes it suitable for some purposes and unsuitable for others

• For example:

  • The half-life of a medical tracer must be long enough to last through the procedure, but short enough to quickly leave the patient’s body and minimize harm

  • The half-life of the alpha source in a smoke alarm must be long enough to ensure steady emissions but not so short that it needs frequent replacement

Calculating half-life

• Scientists can measure the half-lives of different isotopes accurately

• Uranium-235 has a half-life of 704 million years

  • This means it would take 704 million years for the activity of a uranium-235 sample to decrease to half its original amount

• Carbon-14 has a half-life of 5700 years

  • So after 5700 years, there would be 50% of the original amount of carbon-14 remaining

  • After two half-lives or 11 400 years, there would be just 25% of the original amount of carbon-14 remaining

• With each half-life, the amount of undecayed radioactive nuclei remaining decreases by half

A graph can be used to make half-life calculations

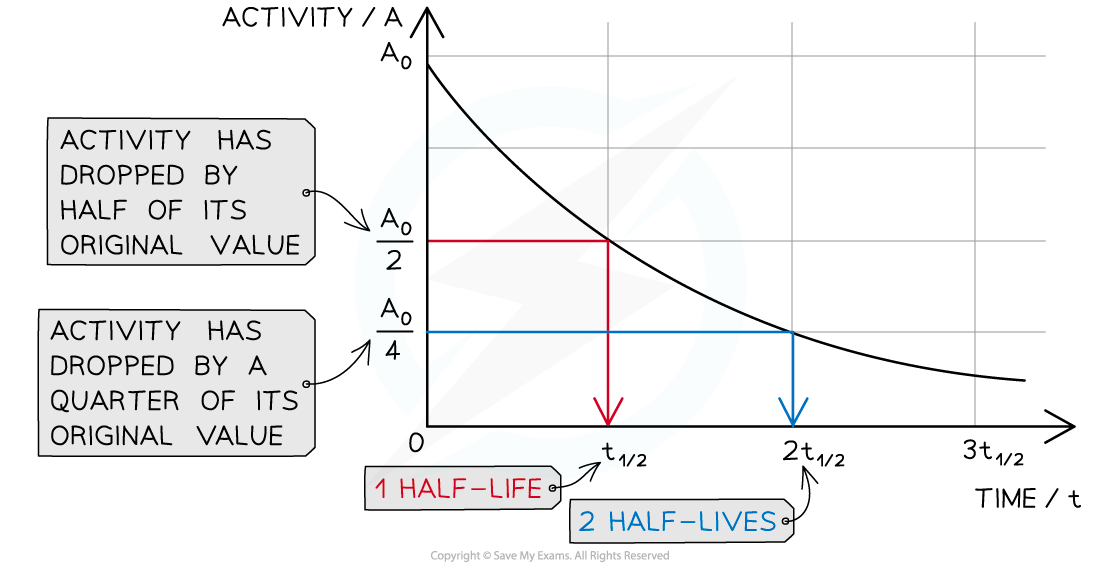
• The time it takes for the activity of the sample to decrease from 100% to 50% is the half-life

• It is the same length of time as it would take to decrease from 50% activity to 25% activity

• The half-life is constant for a particular substance

• The following table shows that as the number of half-life increases, the proportion of the isotope remaining halves

Half life calculation table