Mean & Variance of a CRV (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Mean & variance of a CRV
What are the mean and variance of a continuous random variable?
E(X) is the expected value, or mean, of the continuous random variable X
E(X) can also be denoted by μ
Var(X) is the variance of the continuous random variable X
Var(X) can also be denoted by σ2
The standard deviation, σ, is the square root of the variance
How do I find the mean and variance of a continuous random variable?
The mean is given by
This is given in the exam formula booklet
If the graph of y = f(x) has an axis of symmetry at x = a, then E(X) = a
The variance is given by
This is also given in the exam formula booklet
In the formula note that
from above
So this is equivalent to
The formula booklet also gives the formula
but this is usually not as practical for solving problems
Be careful not to confuse
and
"mean of the squares"
"square of the mean"
Examiner Tips and Tricks
Using your GDC to draw the graph of y = f(x) can highlight any symmetrical properties, and reduce the work involved in finding the mean and variance.
Examiner Tips and Tricks
Don't panic about those infinity symbols in the integrals! basically just means "integrate over all values of
for which
".
E.g. if random variable has the pdf
then the mean is given by
How do I find the mean and variance of a linear transformation of a continuous random variable?
For the continuous random variable X, with mean E(X) and variance Var(X), you can find the mean and variance of the associated random variable aX + b by using
and
Note that adding on a constant b affects the mean, but it doesn't affect the variance
Worked Example
A continuous random variable, X, is modelled by the probability distribution function, f(x), such that
a) Find the mean of X.
Answer:
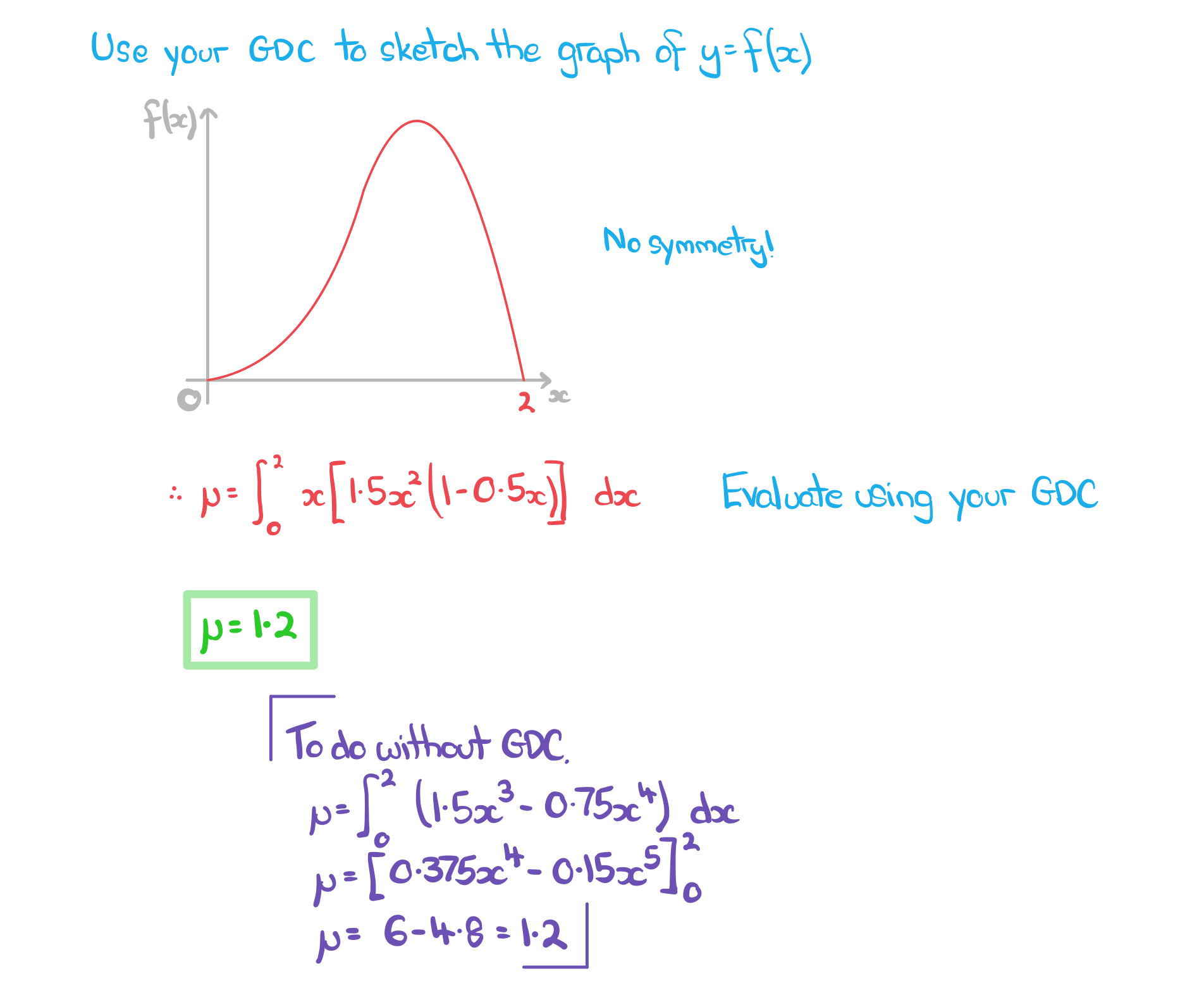
b) Find standard deviation of X.
Answer:
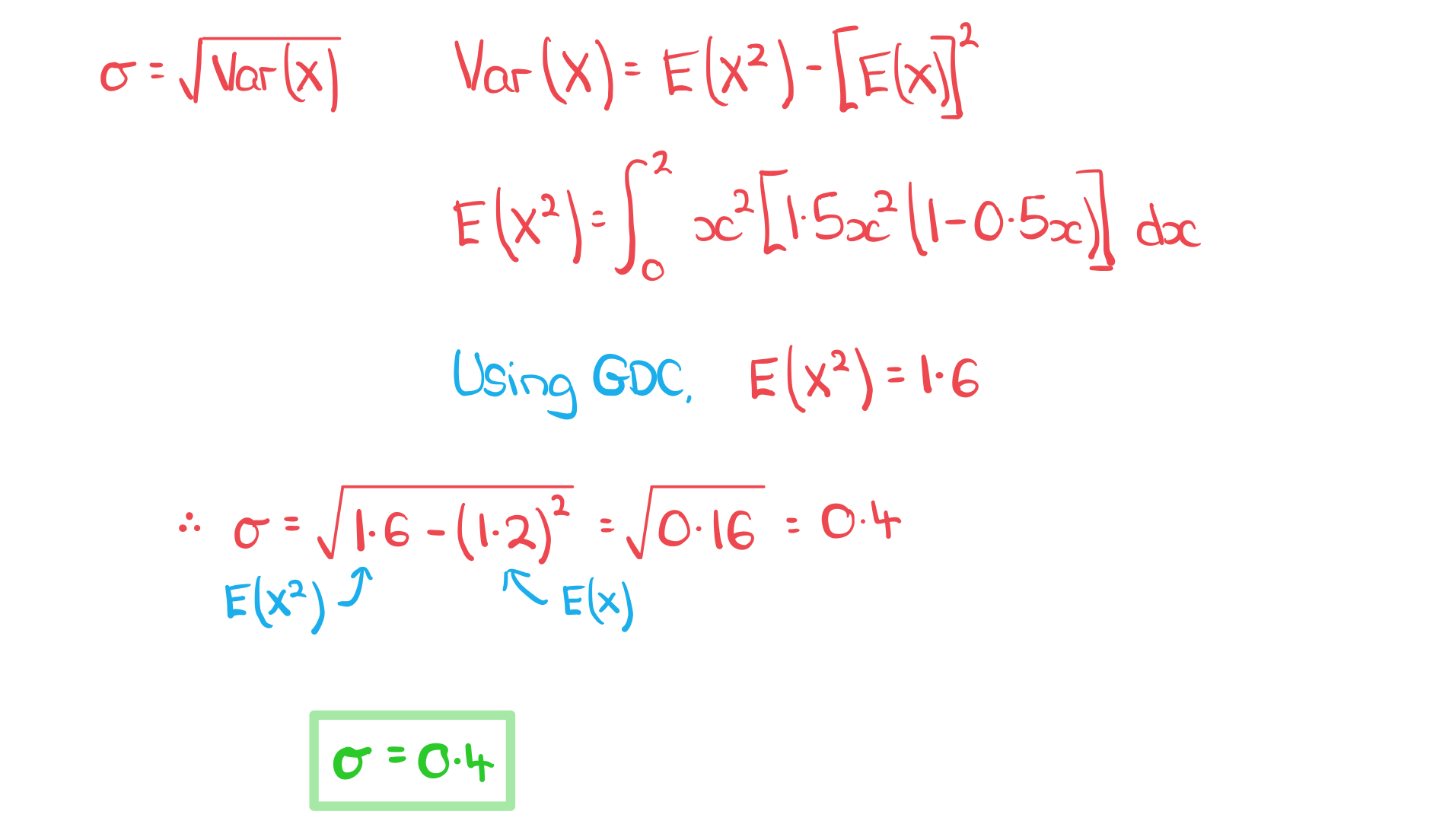

Unlock more, it's free!
Was this revision note helpful?
