Odd & Even Functions (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Odd & even functions
What are odd functions?
A function
is called odd if
for all values of
Examples of odd functions include
Odd powers,
where
e.g.
Some trig functions:
,
,
,
e.g.
Linear combinations of odd functions
e.g.
What are even functions?
A function
is called even if
for all values of
Examples of even functions include
Even powers
where
e.g.
Some trig functions:
,
e.g.
Modulus function
Linear combinations of even functions
e.g.
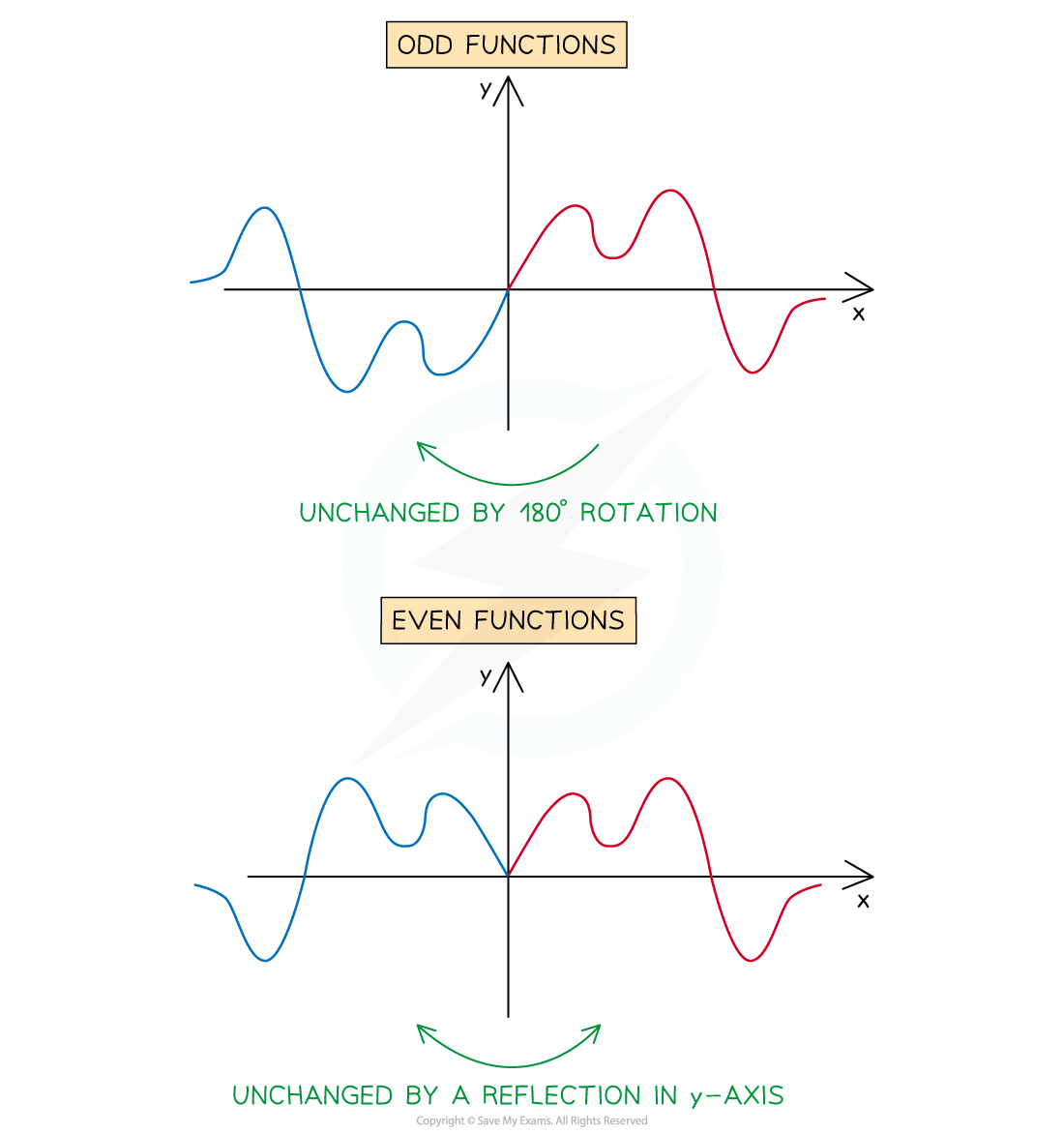
What do the graphs of odd or even functions look like?
The graph of an odd function has rotational symmetry
The graph is unchanged by a 180° rotation about the origin
The graph of an even function has reflective symmetry
The graph is unchanged by a reflection in the y-axis
Examiner Tips and Tricks
You can rotate your GDC by 180° to check if a graph is odd!
Worked Example
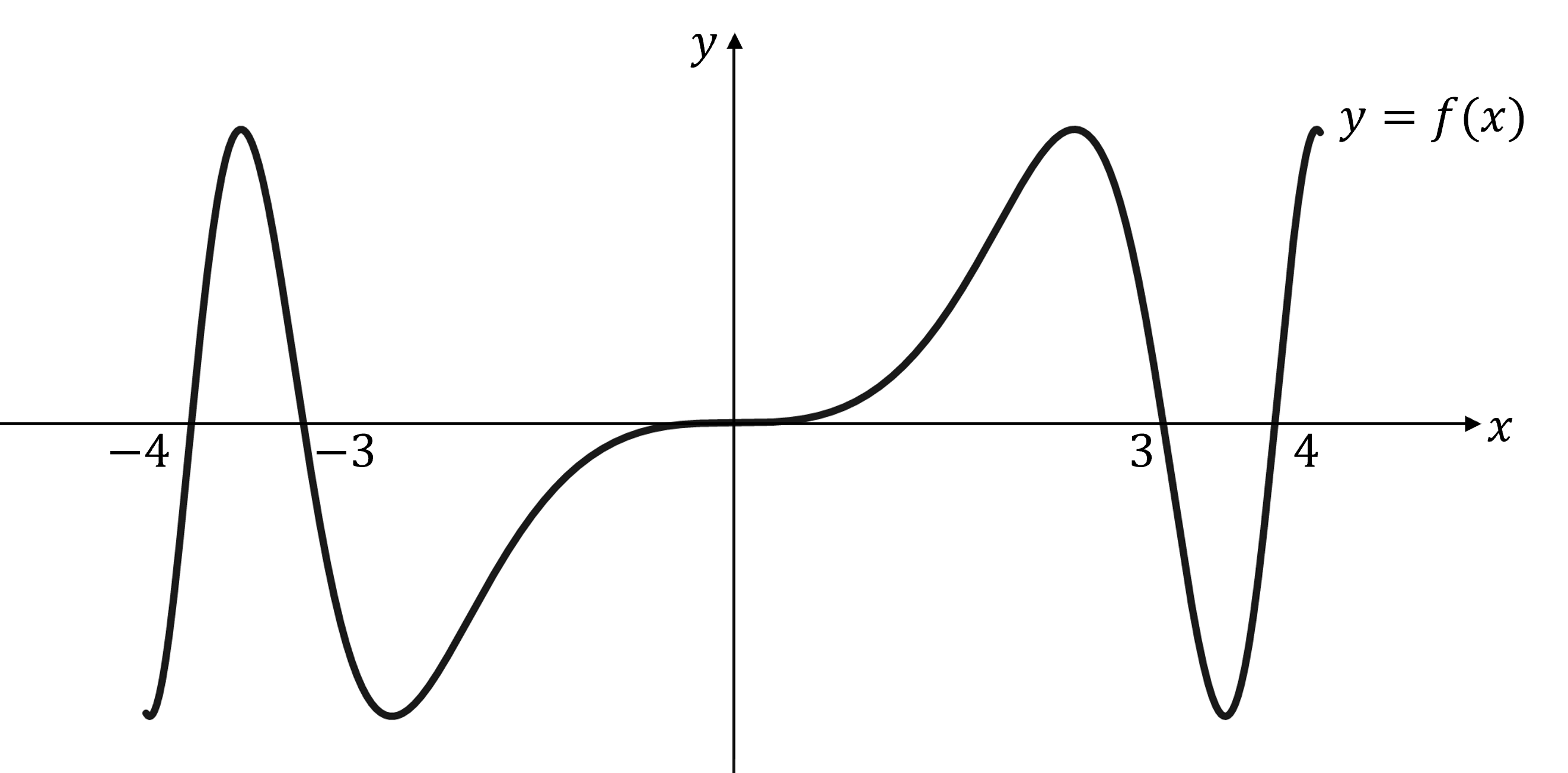
(a) The graph is shown below. State, with a reason, whether the function
is odd or even.

(b) Use algebra to show that is an even function.
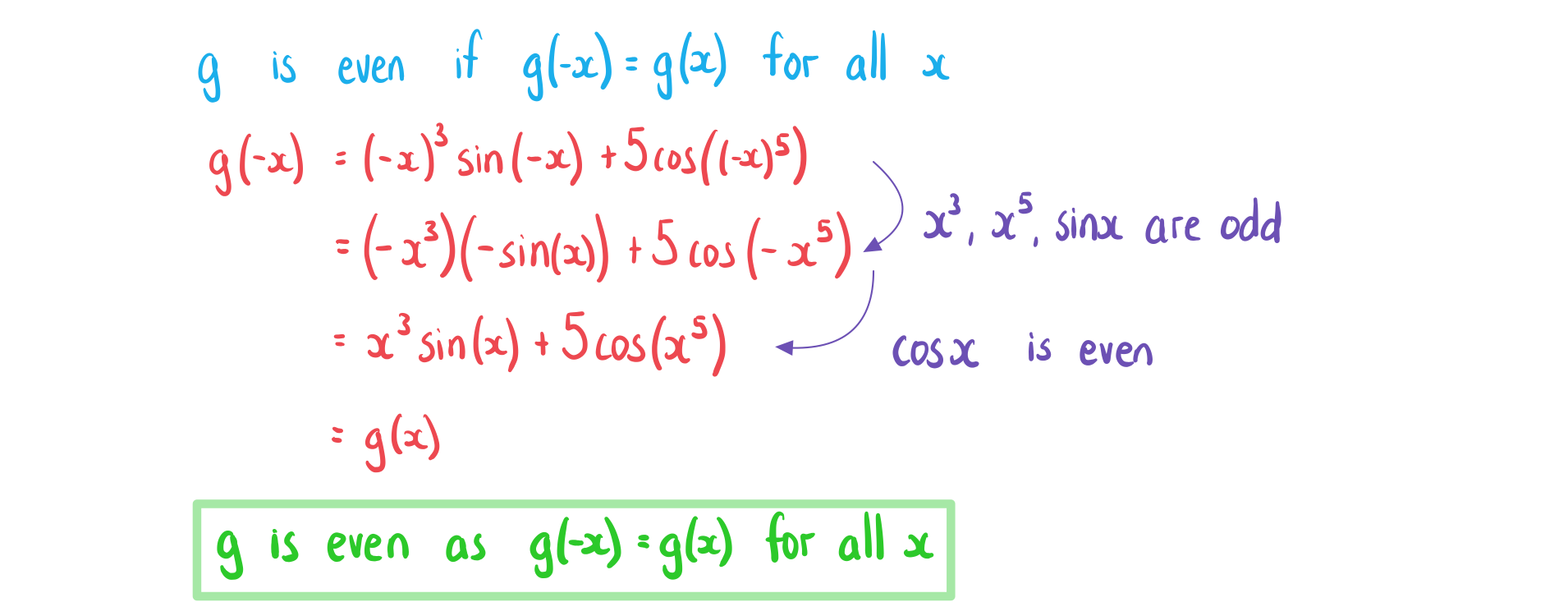

Unlock more, it's free!
Did this page help you?