Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)HLRevision Notes3. Geometry & TrigonometryVector PropertiesAreas using the Vector Product

Areas using the Vector Product (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

DP Analysis & Approaches (AA): HLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): HL

Did this video help you?

Areas using Vector Product

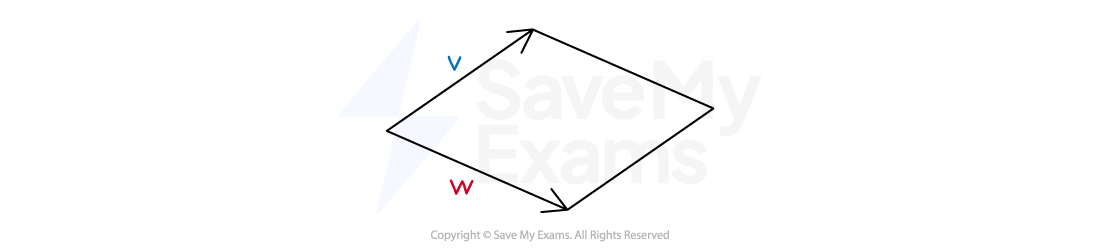
How do I use the vector product to find the area of a parallelogram?

  • The formula for the area of a parallelogram is A equals open vertical bar bold italic v cross times bold italic w close vertical bar

    • bold italic v is the displacement vector for one of the sides

    • bold italic w is the displacement vector for an adjacent side

Rhombus shape with arrows on two sides; top arrow labelled 'V' in blue, bottom arrow labelled 'W' in red, indicating direction or force.
Example of a parallelogram using vectors

Examiner Tips and Tricks

This formula is given in the formula booklet under the geometry and trigonometry section.

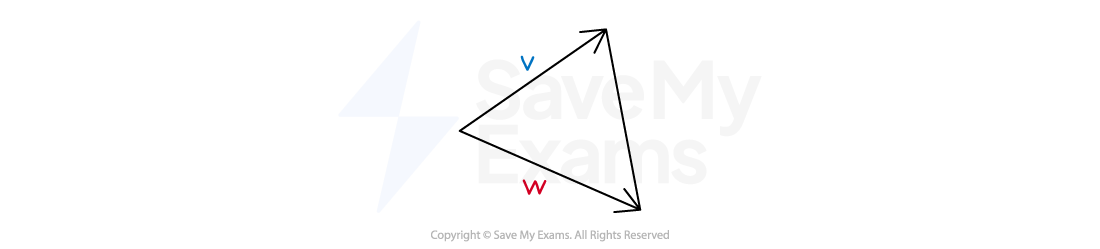
How do I use the vector product to find the area of a triangle?

  • The formula for the area of a triangle is A equals 1 half open vertical bar bold italic v cross times bold italic w close vertical bar

    • bold italic v is the displacement vector for one of the sides

    • bold italic w is the displacement vector for an adjacent side

Diagram of a geometric triangle with two vectors, v in blue pointing up and right, w in red pointing down and right, forming the sides.
Example of a triangle using vectors

Examiner Tips and Tricks

This formula is not given in the formula booklet. You need to remember that you can form a parallelogram by putting two identical triangles together. Therefore, the area of a triangle is half the area of the relevant parallelogram.

Worked Example

Find the area of the triangle enclosed by the coordinates (1, 0, 5), (3, -1, 2) and (2, 0, -1).

3-10-4-ib-aa-hl-area-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:The Vector ProductNext:Geometric Proof with Vectors
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.