Rational Functions with Quadratics (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Quadratic rational functions & graphs
How do I sketch the graph of a rational function where the terms are not linear?
A rational function can be written
Where g and h are polynomials
To find the y-intercept evaluate
To find the x-intercept(s) solve
To find the equations of the vertical asymptote(s) solve
There will also be an asymptote determined by what f(x) tends to as x approaches infinity
In this course it will be either:
Horizontal
Oblique (a slanted line)
This can be found by writing
in the form
You can do this by polynomial division or comparing coefficients
The function then tends to the curve
What are the key features of rational graphs?
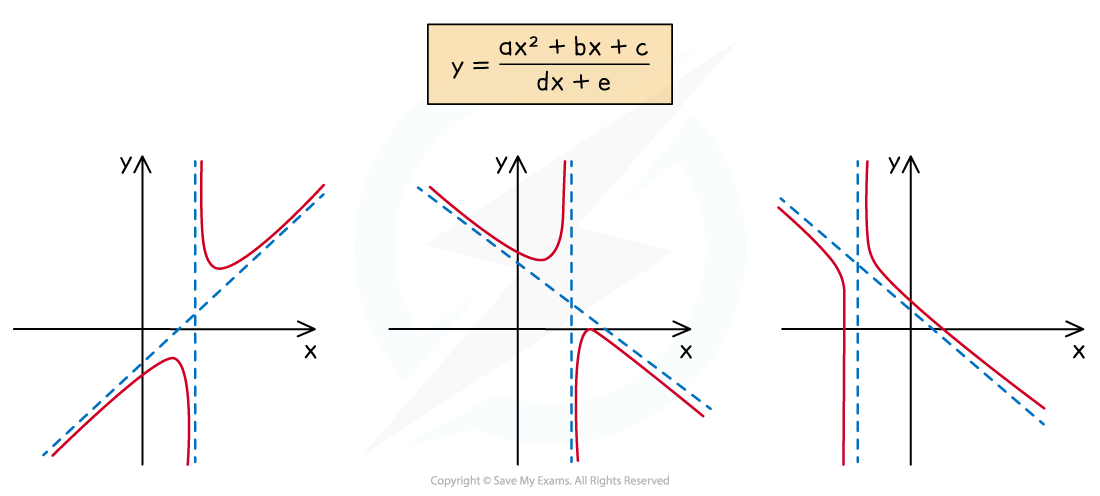
Quadratic over linear
For the rational function of the form
e.g.
The graph has a y-intercept at
provided
e.g. the y-intercept of
is
e.g.
does not have a y-intercept
The graph can have 0, 1 or 2 roots
They are the solutions to
e.g.
has two roots
and
e.g.
has one root
e.g.
has no roots
The graph has one vertical asymptote
e.g. the vertical asymptote of
is
The graph has an oblique asymptote
Which can be found by writing
in the form
Where p, q, r are constants
This can be done by polynomial division or comparing coefficients
e.g.
can be written
the oblique asymptote of
is
Linear over quadratic
For the rational function of the form
e.g.
The graph has a y-intercept at
provided
e.g. the y-intercept of
is
e.g.
does not have a y-intercept
The graph has one root at
e.g. the root of
is
The graph has can have 0, 1 or 2 vertical asymptotes
They are the solutions to
e.g.
has two vertical asymptotes
and
e.g.
has one vertical asymptote
e.g.
has no vertical asymptotes
The graph has a horizontal asymptote at
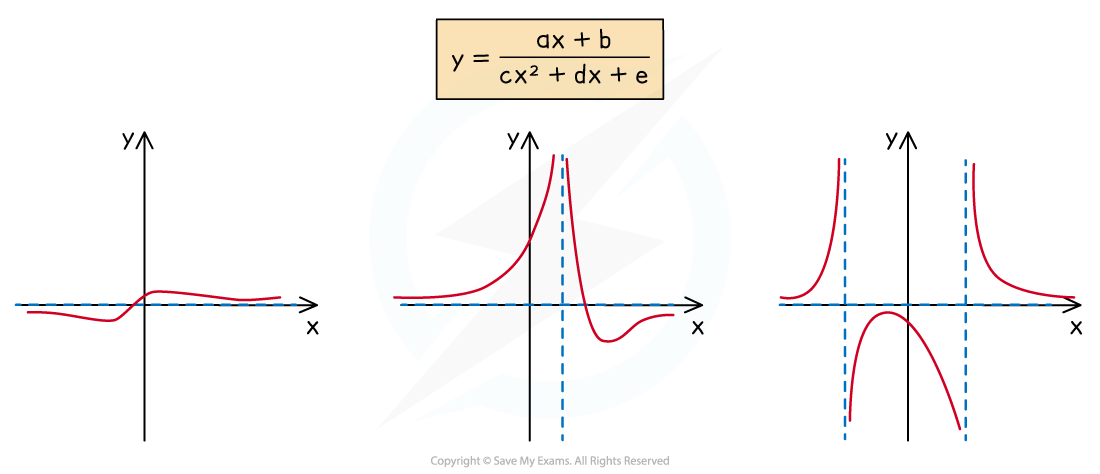
Examiner Tips and Tricks
If you draw a horizontal line anywhere it should only intersect this type of graph twice at most. You can use this idea to check your graph or help you sketch it
Worked Example
The function is defined by
for
.
a)
(i) Show that for constants
and
which are to be found.
(ii) Hence write down the equation of the oblique asymptote of the graph of .
Answer:

b) Find the coordinates of the intercepts of the graph of with the axes.
Answer:

c) Sketch the graph of .
Answer:


Unlock more, it's free!
Was this revision note helpful?
