Basic Limits & Continuity | DP IB Maths: AA HL Revision Notes 2021

Limits

What are limits in mathematics?

When we consider a limit in mathematics we look at the tendency of a mathematical process as it approaches, but never quite reaches, an ‘end point’ of some sort
We use a special limit notation to indicate this

For example $\lim_{x \to 3} f (x)$ denotes ‘the limit of the function f(x) as x goes to (or approaches) 3’

I.e., what value (if any) f(x) gets closer and closer to as x takes on values closer and closer to 3
We are not concerned here with what value (if any) f(x) takes when x is equal to 3 – only with the behaviour of f(x) as x gets close to 3

The sum of an infinite geometric sequence is a type of limit

When you calculate $S_{\infty}$ for an infinite geometric sequence, what you are actually finding is $\lim_{n \to \infty} S_{n}$

I.e., what value (if any) the sum of the first n terms of the sequence gets closer and closer to as the number of terms (n) goes to infinity
The sum never actually reaches $S_{\infty}$ , but as more and more terms are included in the sum it gets closer and closer to that value

In this section of the IB course we will be considering the limits of functions

This may include finding the limit at a point where the function is undefined

For example, $f (x) = \frac{\sin x}{x}$ is undefined when x = 0, but we might want to know how the function behaves as x gets closer and closer to zero

Or it may include finding the limit of a function f(x) as x gets infinitely big in the positive or negative direction

For this type of limit we write $\lim_{x \to \infty} f (x)$ or $\lim_{x \to - \infty} f (x)$ (the first one can also be written as $\lim_{x \to + \infty} f (x)$ to distinguish it from the second one)

These sorts of limits are often used to find the asymptotes of the graph of a function

How do I find a simple limit?

STEP 1: To find $\lim_{x \to a} f (x)$ begin by substituting a into the function f(x)

- If f(a) exists with a well-defined value, then that is also the value of the limit
- For example, for $f (x) = \frac{x - 1}{x}$ we may find the limit as x approaches 3 like this:

$\lim_{x \to 3} f (x) = \lim_{x \to 3} \frac{x - 1}{x} = \frac{3 - 1}{3} = \frac{2}{3}$

- - In this case, $\lim_{x \to 3} f (x)$ is simply equal to f(3)
STEP 2: If f(a) does not exist, it may be possible to use algebra to simplify f(x) so that substituting a into the simplified function gives a well-defined value
- In that case, the well-defined value at x = a of the simplified version of the function is also the value of the limit of the function as x goes to a
- For example, $f (x) = \frac{x^{2}}{x}$ is not defined at x = 0, but we may use algebra to find the limit as x approaches zero:

$\lim_{x \to 0} f (x) = \lim_{x \to 0} \frac{x^{2}}{x} = \lim_{x \to 0} \frac{x}{1} (cancelling the x^{'} s) = \frac{0}{1} = 0$

Note that $f (x) = \frac{x^{2}}{x}$ and $g (x) = x$ are not the same function!
They are equal for all values of x except zero
But for x = 0, g(0) = 0 while f(0) is undefined
However f(x) gets closer and closer to zero as x gets closer and closer to zero

If neither of these steps gives a well-defined value for the limit you may need to consider more advanced techniques to evaluate the limit

For example l’Hôpital’s Rule or using Maclaurin series

How do I find a limit to infinity?

As x goes to $+ \infty$ or $- \infty$ , a typical function f(x) may converge to a well-defined value, or it may diverge to $+ \infty$ or $- \infty$

Other behaviours are possible – for example $\lim_{x \to \infty} \sin x$ is simply undefined, because sin x continues to oscillate between 1 and -1 as x gets larger and larger

There are two key results to be used here:

$\lim_{x \to \pm \infty} \frac{k}{x^{n}}$ converges to 0 for all n >0 and all $k \in ℝ$
$\lim_{x \to + \infty} x^{n}$ diverges to $+ \infty$ for all n > 0

$\lim_{x \to - \infty} x^{n}$ for n > 0 will need to be considered on a case-by-case basis, because of the differing behaviour of xⁿ for different values of n when x is negative

STEP 1: If necessary, use algebra to rearrange the function into a form where one or the other of the key results above may be applied

STEP 2: Use the key results above to evaluate your limit
For example:

$\lim_{x \to \infty} \frac{3 x^{2} - 2 x + 1}{4 x^{2} - x + 2} = \lim_{x \to \infty} \frac{3 - \frac{2}{x} + \frac{1}{x^{2}}}{4 - \frac{1}{x} + \frac{2}{x^{2}}} = \frac{3 - 0 + 0}{4 - 0 + 0} = \frac{3}{4}$

$\lim_{x \to + \infty} \frac{x^{2} + 5 x - 2}{32 x + 3} = \lim_{x \to + \infty} \frac{x + 5 - \frac{2}{x}}{32 + \frac{3}{x}} = \frac{(+ \infty) + 5 - 0}{32 + 0} = + \infty$

I.e., the limit diverges to $+ \infty$ (because $\frac{x^{2} + 5 x - 2}{32 x + 3}$ it gets bigger and bigger without limit as x gets bigger and bigger)

Remember that neither $\frac{0}{0}$ nor $\frac{\pm \infty}{\pm \infty}$ has a well-defined value!

If you attempt to evaluate a limit and get one of these two forms, you will need to try another strategy
This may just mean different or additional algebraic rearrangement
But it may also mean that you need to consider using l’Hôpital’s Rule or Maclaurin series to evaluate the limit

It is also worth remembering that if $\lim_{x \to \infty} f (x) = \infty$ , then $\lim_{x \to \infty} \frac{k}{f (x)} = 0$ for any non-zero $k \in ℝ$

This can be useful for example when evaluating the limits of functions containing exponentials

$\lim_{x \to \infty} e^{p x} = \infty$ for any p > 0, so we immediately have $\lim_{x \to \infty} e^{- p x} = \lim_{x \to \infty} \frac{1}{e^{p x}} = 0$ for p > 0
See the worked example below for a more involved version of this

Do limits ever have ‘directions’?

Yes they do!

The notation $\lim_{x \to a^{+}} f (x)$ means ‘the limit of f(x) as x approaches a from above’

I.e., this is the limit as x comes ‘down’ towards a, only considering the function’s behaviour for values of x that are greater than a

The notation $\lim_{x \to a^{-}} f (x)$ means ‘the limit of f(x) as x approaches a from below’

I.e., this is the limit as x comes ‘up’ towards a, only considering the function’s behaviour for values of x that are less than a

One place these sorts of limits appear is for functions defined piecewise

In this case the limits ‘from above’ and ‘from below’ may well be different for values of x at which the different ‘pieces’ of the function are joined

But also be aware of a situation like the following, where the limits from above and below may also be different:

$\lim_{x \to 0^{+}} \frac{1}{x} = + \infty$ (because $\frac{1}{x} > 0$ for x > 0, with $\frac{1}{x}$ becoming bigger and bigger in the positive direction as x gets closer and closer to zero ‘from above’)
$\lim_{x \to 0^{-}} \frac{1}{x} = + \infty$ (because $\frac{1}{x} < 0$ for x < 0, with $\frac{1}{x}$ becoming bigger and bigger in the negative direction as x gets closer and closer to zero ‘from below’)
The graph of $y = \frac{1}{x}$ shows this limiting behaviour as x approaches zero from the two different directions

Worked example

Consider the function

f (x) = \frac{3 - 4 x - 5 x^{4}}{2 x^{4} + x^{3} + 7}

find

\lim_{x \to \infty} f (x)

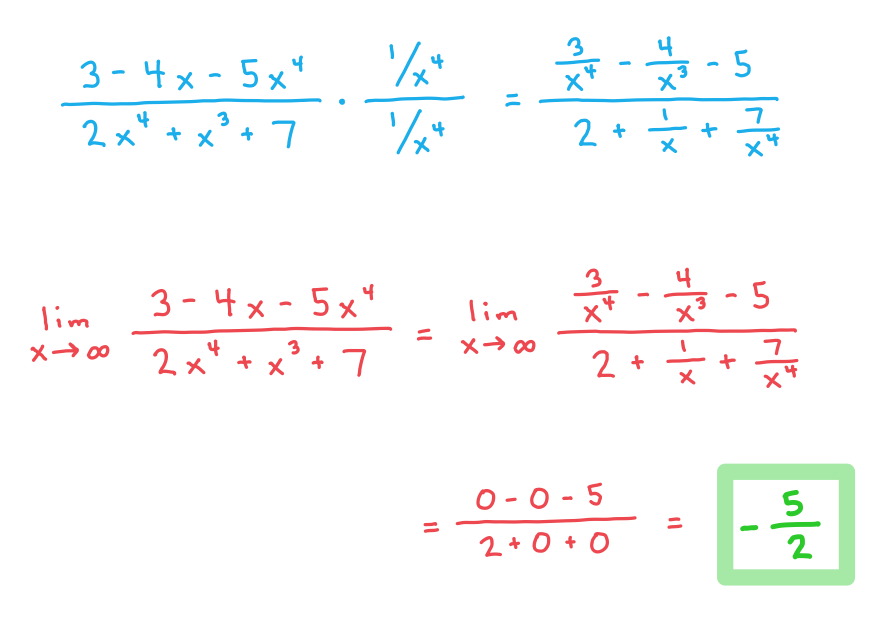
5-7-1-ib-aa-hl-limits-a-we-solution

Consider the function

$g (x) = \{\begin{matrix} \frac{1 - 5 x}{x^{2}}, & x < 5 \\ x^{2} - 4 x - 6, & x \geq 5 \end{matrix}$

find (i)

\lim_{x \to 5^{-}} g (x)

, and (ii)

\lim_{x \to 5^{+}} g (x)

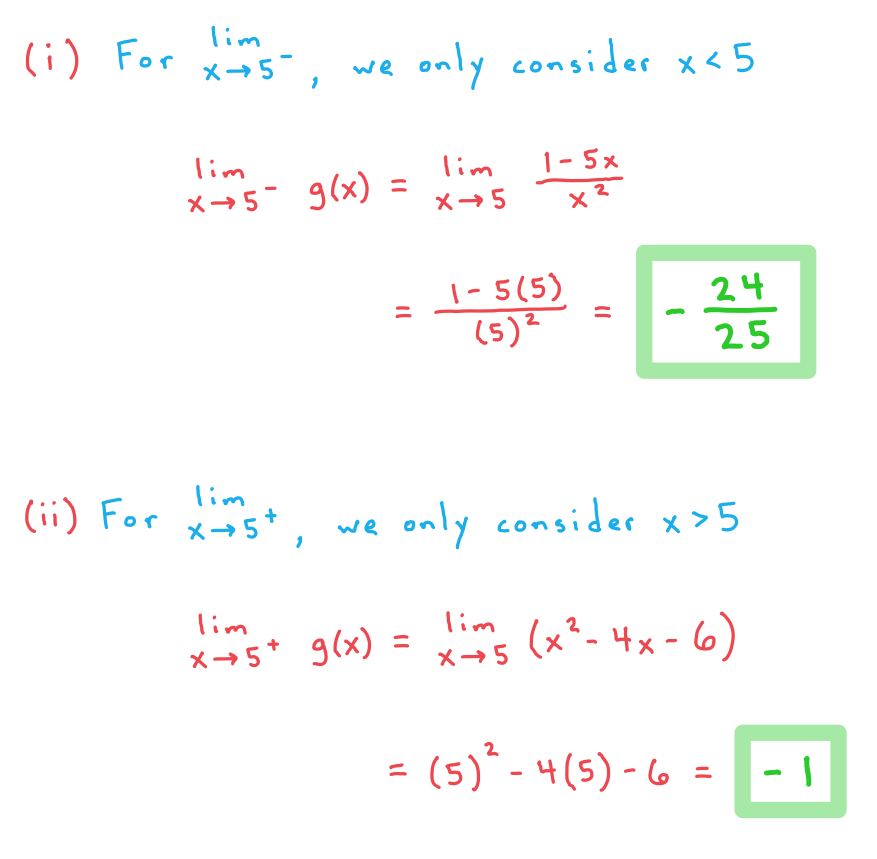
5-7-1-ib-aa-hl-limits-b-we-solution

Consider the function

h (x) = \frac{2 e^{3 x} - 3}{4 - 5 e^{3 x}}

find

\lim_{x \to \infty} h (x)

5-7-1-ib-aa-hl-limits-c-we-solution

Continuity & Differentiability

What does it mean for a function to be continuous at a point?

If a function is continuous at a point then the graph of the function does not have any ‘holes’ or any sudden ‘leaps’ or ‘jumps’ at that point
- One way to think about this is to imagine sketching the graph
  - So long as you can sketch the graph without lifting your pencil from the paper, then the function is continuous at all the points that your sketch goes through
  - But if you would have to lift your pencil off the paper at some point and continue drawing the graph from another point, then the function is not continuous at any such points where the function ‘jumps’

5-7-1-ib-aa-hl-cont-_-diff_contin-exx

There are two main ways a function can fail to be continuous at a point:
- If the function is not defined for a particular value of x then it is not continuous at that value of x
  - For example, $f (x) = \frac{1}{x}$ is not continuous at x = 0
- If the function is defined for a particular value of x, but then the value of the function ‘jumps’ as x moves away from that x value in the positive or negative direction, then the function is not continuous at that value of x
  - This type of discontinuity can occur in a piecewise function, for example, where the different pieces of the function’s graph don’t ‘join up’
You can use limits to show that a function is continuous at a point
- Let f(x) be a function defined at x = a, such that f(a) = b
  - If $\lim_{x \to a^{-}} f (x) = b$ and $\lim_{x \to a +} f (x) = b$ , then f(x) is continuous at x = a
  - If either of those limits is not equal to b, then f(x) is not continuous at x = a
- This is a slightly more formal way of expressing the ‘you don’t have to lift your pencil from the paper’ idea!

What does it mean for a function to be differentiable at a point?

We say that a function f(x) is differentiable at a point with x-coordinate x₀, if the derivative f’(x) exists and has a well-defined value f’(x₀) at that point

To be differentiable at a point a function has to be continuous at that point

So if a function is not continuous at a point, then it is also not differentiable at that point

But continuity by itself does not guarantee differentiability

- This means that differentiability is a stronger condition than continuity
- If a function is differentiable at a point, then the function is also continuous at that point
- But a function may be continuous at a point without being differentiable at that point
- This means there are functions that are continuous everywhere but are not differentiable everywhere
In addition to being continuous a point, differentiability also requires that the function be smooth at that point
- ‘Smooth’ means that the graph of the function does not have any ‘corners’ or sudden changes of direction at the point
- An obvious example of a function that is not smooth at certain points is a modulus function |f(x)| at any values of x where f(x) changes sign from positive to negative
  - At any such point a modulus function will not be differentiable

5-7-1-ib-aa-hl-cont-_-diff_smooth-exx

Examiner Tip

On the exam you will not usually be asked to test a function for continuity at a point

You should however be familiar with the basic ideas about continuity outlined above

On the exam you will not be asked to test a function for differentiability at a point

You should however be familiar with the basic ideas about differentiability and its relationship with continuity as outlined above

Worked example

Consider the function $f$ defined by

$f (x) = \{\begin{matrix} x^{2} - 2 x - 1, & x < 3 \\ 2 & x = 3 \\ \frac{x + 2}{2}, & x > 3 \end{matrix}$

use limits to show that

f

is not continuous at

x = 3

5-7-1-ib-aa-hl-cont--diff-a-we-solution

Hence explain why

f

cannot be differentiable at

x = 3

5-7-1-ib-aa-hl-cont--diff-b-we-solution

Basic Limits & Continuity (DP IB Maths: AA HL)

Revision Note

Limits

What are limits in mathematics?

How do I find a simple limit?

How do I find a limit to infinity?

Do limits ever have ‘directions’?

Worked example

Continuity & Differentiability

What does it mean for a function to be continuous at a point?

What does it mean for a function to be differentiable at a point?

Examiner Tip

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Roger