Differentiating Powers of x (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Differentiating powers of x
What is differentiation?
Differentiation is the process of finding an expression for the derivative (gradient function) of a function from an expression for the function
How do I differentiate powers of x?
Powers of
are differentiated according to the following formula:
If
then
where
This is given in the formula booklet
If the power of
term is multiplied by a constant then the derivative is also multiplied by that constant
If
then
where
and
is a constant
The alternative notation (to
) is to use
If
then
e.g. If
then
Don't forget these two special cases:
If
then
e.g. If
then
If
then
e.g. If
then
Functions involving roots will need to be rewritten as fractional powers of
first
e.g. If
then rewrite as
and differentiate
Functions involving fractions with denominators in terms of
will need to be rewritten as negative powers of
first
e.g. If
then rewrite as
and differentiate
How do I differentiate sums and differences of powers of x?
For an expression that is a sum or difference of powers of
, just differentiate term by term
e.g. If
then
Products and quotients cannot be differentiated in this way so would need expanding/simplifying first
e.g. If
then expand to
which is a sum/difference of powers of
and can be differentiated
Examiner Tips and Tricks
A common mistake is not simplifying expressions before differentiating.
For example, the derivative of can not be found by multiplying the derivatives of
and
.
Worked Example
The function is given by
, where
Find the derivative of
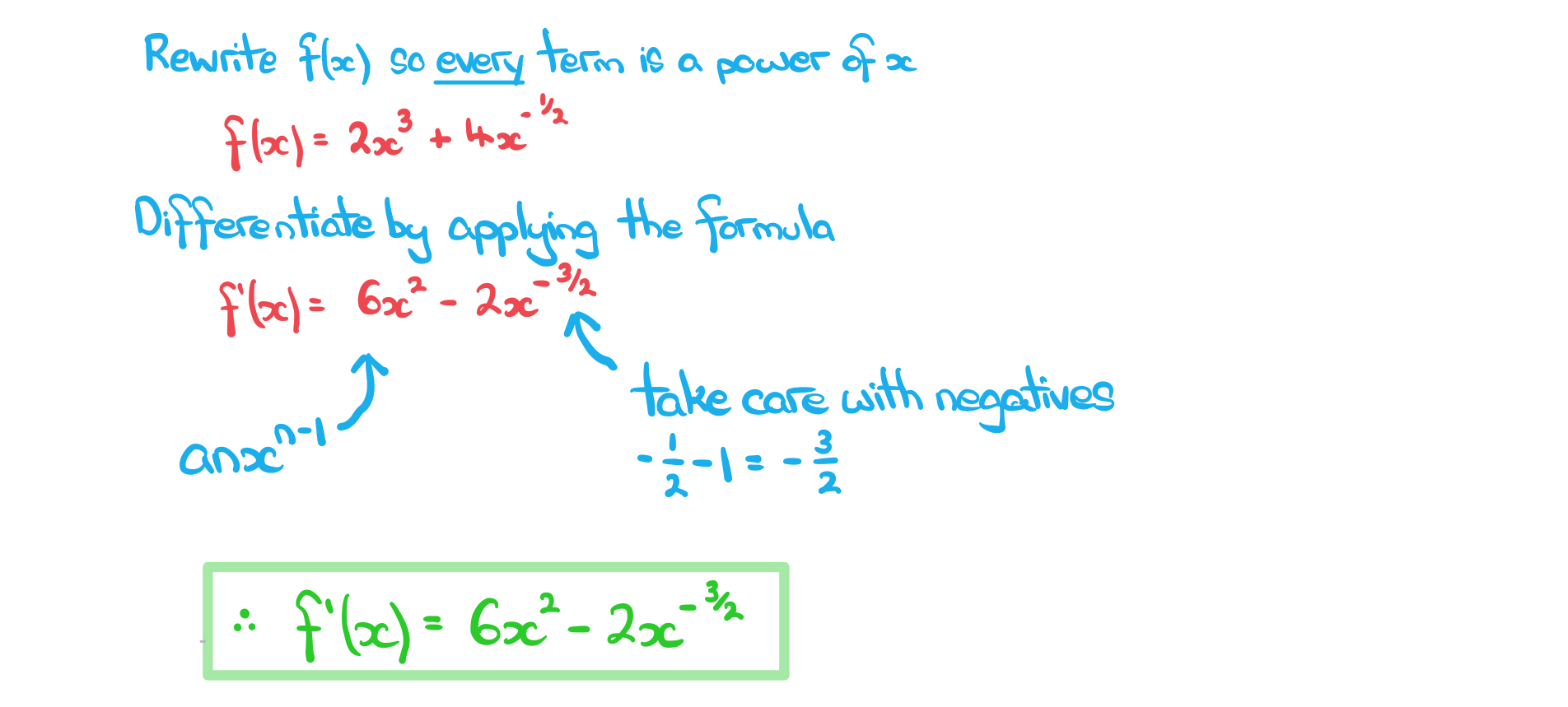

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?